[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Prendo le mosse da un famoso problema (ricreativo)
la cui più antica versione risale probabilmente ad Ozanam-Montucla,
1778: "Avec cinq carrés égaux, en former un seul."
Questo problema è stato discusso recentemente (giugno 2001)
nella mailing list del S.I.G. Giochi.
1. Dividere un quadrato in cinque quadrati uguali.
I problemi di dissezione, come questo, richiedono di ritagliare la figura di partenza in un certo numero di pezzi e di ricomporre tali pezzi in modo da ottenere la figura o le figure di arrivo.
Un metodo divertente per risolvere questo problema (valido in genere per i problemi di dissezione) consiste in questo:
Si disegna un quadrato di area = 5 (lato = rad(5)) su un foglio di carta;
Si disegna un reticolo, ad es. 4x4, di quadratini di area = 1 (lato = 1) su un foglio di acetato trasparente. Anche se i disegni non sono "super precisi", il metodo (in questo caso) funziona abbastanza bene.
Si sovrappone il foglio di acetato al foglio di carta in modo da vedere il quadrato grande sotto il reticolo di quadratini.
Si sposta e si ruota il foglio di acetato fino a trovare una configurazione che sembra risolvere il problema (questa è la parte più divertente).
Si verifica la soluzione dal punto di vista matematico.
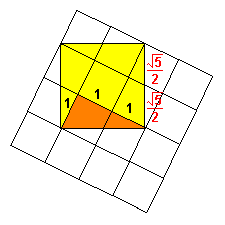
La figura qui sotto illustra un possibile
risultato.
Il quadrato colorato ha area = 5 e, di conseguenza, lato = rad(5)

Il quadrato giallo + arancione risulta suddiviso
in 9 pezzi: un quadratino centrale e altri 8 pezzi. Unendo questi
ultimi a 2 a 2 si ottengono 4 quadratini uguali a quello centrale.
In tutto 5 quadratini uguali.
La verifica matematica si basa sul teorema di Pitagora.
Il metodo dell'acetato deriva da un'idea di Harry
Lingden nel 1961.
Harry Lingden è un Grande Maestro delle
dissezioni piane ed è stato capace di trasformare, ad esempio,
una croce di Malta in un quadrato in soli 7 pezzi.
Giocando con queste figure ho trovato altre due configurazioni che mi hanno posto alcuni problemi.
Ricordo che il quadrato colorato ha area 5 e i
quadratini del reticolo hanno area 1.
La figura qui sotto è una delle configurazioni che potrebbero
risolvere il problema.
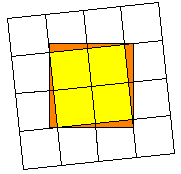
2. La domanda è: è possibile costruire un quadrato con i quattro triangoli rettangoli arancioni e con un numero finito di tagli?
Ecco un'altra configurazione problematica.
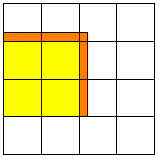
La figura arancione a forma di L si chiama gnomon.
Uno gnomon è una figura che unita ad un'altra
figura genera una figura simile alla prima.
La "L" arancione quindi è uno gnomon del quadrato
giallo perché unita ad esso forma un nuovo quadrato, ovviamente
simile al primo. Il quadrato giallo, invece, non è uno gnomon
della "L", perché non può essere unito ad essa in
modo da formare un'altra "L".
3. Osservando la figura si capisce che
l'area dello gnomon è 1. Ed ecco il mio problema:
E' possibile trasformare lo gnomon in un quadrato con un numero
finito di tagli?
Se no, dimostrare perché, se sì, mostrare come.
Desidero precisare che non ho trovato la risposta dei due problemi posti per cui ogni contributo è ben accetto.
Altri problemi sulla dissezione del quadrato.
4. Dividere un quadrato in 7 quadrati uguali.
5. Per quali n è possibile dividere un quadrato in n quadrati uguali?
6. Trasformare un rettangolo 5 * 1 in un quadrato, tagliandolo in 5 pezzi.
2. La domanda è: è possibile costruire
un quadrato con i quattro triangoli rettangoli arancioni e con un
numero finito di tagli?
Un particolare ringraziamento ad
Andrea Girelli per la seguente risoluzione.

Si proceda come segue. Sia 1 il lato di un singolo quadrato
giallo. Un triangolo rettangolo arancione avrà ipotenusa pari a
2 (come si evince dalla figura). Dovendo essere la somma delle
aree dei quattro triangoli arancioni pari a 1, detta h l'altezza
di uno di tali triangoli relativa all'ipotenusa avremo:
Area arancione = 4*(Area triangolo arancione) 1 = 4*(2*h/2) da
cui h=1/4.
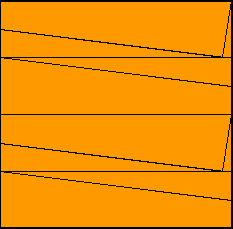
Prendiamo due triangoli arancioni e disponiamoli come segue:

Si tagli quindi lungo l'altezza h e si porti il nuovo pezzo
"dall'altra" parte come sotto:

Abbiamo ottenuto in tal modo un rettangolo di lati 2*0,25.
Dividiamo a metà tale rettangolo in altri due di lati 1*0,25 e 1*0,25,
e operiamo nello stesso modo con gli altri due rettangoli
rimanenti. Impilandoli poi nel verso delle altezze otteniamo un
quadrato 1*1, come da figura:
3. E' possibile trasformare lo gnomon in
un quadrato con un numero finito di tagli?
Se no, dimostrare perché, se sì, mostrare come.
Un particolare ringraziamento ad
Andrea Girelli per la seguente risoluzione.

Sia l il lato del quadrato originario e x lo spessore più piccolo dello gnomon. L'area dello gnomon sarà x^2+2xl. Essendo l'area del quadrato originario pari a 4 (quindi l=2), mentre l'area dello gnomon pari a 1, avremo:
x^2+2xl = x^2+4x = 1
x^2+4x-1 =0
che ammette come soluzione valida x=-2+sqr(5).
Solo a titolo di verifica si osserva che è possibile costruire con lo gnomon un rettangolo di lati sqr(5)-2 e sqr(5)+2, ossia di area (sqr(5)-2)*(sqr(5)+2) = 1 (come ci si aspettava :))
Per la soluzione si osservi la figura qui sotto.
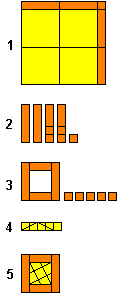
Tagliamo lo gnomon in modo da formare 1 quadrato
di lato x e 4 rettangoli di lati x ed l/2 (è sufficiente seguire
le linee guida).
Da due dei rettangoli togliamo 2 quadrati di lato x ciascuno.
Prendiamo i quattro rettangoli così ottenuti e mettiamoli sui
bordi interni di un quadrato di lato l/2 (ossia 1). In tal modo
all'interno di questo quadrato vi sarà un buco quadrato di area
1-4*l/2*x + 4*x^2, che dovrà essere riempito coi 5 quadrati di
lato x^2 rimasti fuori (ovviamente se eguagliamo le due aree
troviamo la nostra prima equazione).
Quello che dobbiamo fare adesso è costruire un quadrato dai 5
quadrati con un numero finito di tagli, ovvero costruire da un
quadrato altri 5 uguali fra loro con un numero finito di tagli,
ovvero risolvere a scelta:
a) il problema 2
b) il problema 1 (questa soluzione è illustrata in figura)
b) questo stesso problema allo stesso modo (in tal caso la
procedura diventa ricorsiva).
4. Dividere un quadrato in 7 quadrati uguali.
5. Per quali n è possibile dividere un quadrato in n quadrati uguali?
6. Trasformare un rettangolo 5 * 1 in un quadrato, tagliandolo in 5 pezzi.
Sito Web realizzato da Gianfranco Bo