[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Ricreazioni di Dicembre 2001
![]()
182. e^x, l'indistruttibile
proposto da Dario Ripamonti
Vagabondando nel sito, ho trovato una barzelletta su e^x.
Ne conosoco un'altra versione.
Ad un certo punto, entra la derivata, e tutte le funzioni fuggono impaurite.
e^x fa finta di niente, confidando nella sua invulnerabilità.
Quand'ecco che la derivata urla "derivata rispetto a y".
>>> Risposte & riflessioni
![]()
181. Indovinello di Natale
proposto da Mimmo
In un bosco c'è un cesto con tre funghi.
Arrivano tre gnomi e, ogni gnomo prende un fungo.
Quando vanno via, nel cesto rimane un fungo.
Come mai?.
>>> Risposte & riflessioni
.
.
.
.
.
Mimmo
L'ultimo gnomo ha preso il cesto con il fungo rimasto.
![]()
180. 12 palline super-difficile
proposto da Massimo Giorgi
Nel famoso problema delle 12 palline, già
proposto in questo sito da Alberto Fabrizi, NON SI CHIEDE di individuare, oltre
alla pallina difettosa, anche IL DIFETTO ovvero se essa pesa di più o di meno
delle altre.
Vi propongo invece la mia VARIANTE del problema ed una possibile
soluzione.
Le 12 Palline (Variante con maggiori difficoltà)
Abbiamo 12 palline che sembrano identiche ma non lo sono. Una di esse
ha un peso diverso dalle altre ma non sappiamo qual è e neppure se è più
pesante o più leggera delle altre. Dobbiamo scoprire qual è e
se pesa di più o di meno delle altre con 3 pesate comparative
utilizzando una bilancia a bracci uguali.
Ah, dimenticavo: non abbiamo i pesi.
>>> Risposte &
riflessioni
Massimo Giorgi
Questa soluzione riprende, con le opportune modifiche, la
soluzione già data da Alberto Fabrizi in questo sito.
Le modifiche sono evidenziate in rosso.
Definiamo BUONE le 11 palline di eguale peso e <D> la
pallina di peso diverso.
Osserviamo preliminarmente che:
Osservazione A: qualora si sapesse che <D> abbia peso maggiore (o minore)
basterebbe una sola pesata per individuarla fra tre palline.
Si proceda dunque nel modo seguente.
Si pongano su ciascuno dei due piatti quattro palline. Possono verificarsi due
casi:
1° caso: i due gruppi di 4 palline hanno lo stesso peso;
2° caso: i due gruppi di 4 palline hanno peso diverso.
Esaminiamo ora i due casi possibili.
1° caso: i due gruppi di 4 palline hanno lo stesso peso;
Se hanno peso uguale, abbiamo costituito una riserva di otto
"buone", e <D> sta tra le altre quattro. Confrontiamo
tre di quest'ultime con tre "buone": se il peso è uguale, <D>
è quella scartata e confrontandola con una "buona" nella terza pesata
sappiamo anche se essa è più leggera o più pesante delle altre. Se viceversa
il piatto con le tre nuove palline risulta più leggero (o più pesante)
sappiamo automaticamente che <D> è più leggera (o più pesante) e per
l'osservazione A la possiamo individuare con la terza pesata.
2° caso: i due gruppi di 4 palline hanno peso diverso.
Se dalla prima pesata il piatto sinistro risulta più pesante del
destro, abbiamo una riserva di quattro buone. Dette SSSS le palline che sono
state pesate nel piatto sinistro, DDDD quelle pesate nel piatto destro e BBBB
quelle buone, operiamo la seconda pesata nel seguente modo: DSSS - SBBB (abbiamo
scambiato di piatto due palline, D e S,
e sostituito tre palline del piatto destro con tre buone).
A questo punto si hanno 3 sotto-casi.
1) Se il piatto sinistro continua a essere più pesante, sappiamo che <D> è una delle tre SSS dello stesso piatto, e sappiamo anche che la falsa è più pesante; con la terza pesata possiamo individuarla (per l'osservazione A).
2) Se invece i piatti alla seconda pesata registrano lo stesso peso, sappiamo che <D> è una delle tre DDD sostituite sul piatto destro con tre buone, e sappiamo anche che <D> è più leggera; perciò <D> può essere individuata con la terza pesata (osservazione A).
3) Se infine il piatto sinistro diviene più leggero, <D> è una delle due palline scambiate da un piatto all'altro, S o D, ma ancora non sappiamo se sia S più pesante oppure D più leggera (Nota che il contrario non può accadere!). Facciamo allora la terza pesata nel seguente modo: BSSS - SBBB (sostituiamo D con una buona). Possono verificarsi due sotto-sotto-casi.
3.1) I due piatti hanno lo stesso peso: vuol dire che la pallina difettosa è D (quella sostituita) e che è più leggera delle altre;
3.2) Il piatto sinistro continua ad essere più leggero: vuol dire che la pallina difettosa è S (quella rimasta sul piatto destro) e che è più pesante delle altre.
![]()
179. Rettificazione della circonferenza
proposto da Pighin
Ho trovato su una rivista una interessante asserzione di
Archimede sulla quadratura del cerchio.
E' descritta nella figura allegata
Spero di non essere incappato in un problema troppo difficile.
Calcolando il valore numerico della tangente con sempre maggiore precisione con
metodi numerici (Excel+macro) i conti tornano.
Non riesco a trovare una dimostrazione formale, spero che qualcuno mi possa
aiutare

Archimede afferma: la lunghezza della circonferenza è uguale a quella dell'asse in rosso.
La curva in nero è una spirale di Archimede.
La tangente alla spirale è quella corrispondente all'angolo di 360°
>>> Risposte &
riflessioni
Gianfranco Bo
Questo problema ci dà un'ottima occasione di nutrirci alle fonti dei
Grandi Maestri.
La proposizione citata è la n. 18 del libro "SPIRALI"
di Archimede.
In versione originale suona più o meno così:
"Se una linea retta è tangente ad una spirale, nella prima rotazione, nel termine della spirale stessa, e se dal punto che è principio della spirale si conduce una retta perpendicolare alla retta principio della rotazione, la retta così condotta incontra la tangente, e il segmanto di retta compreso fra la tangente e il principio della spirale sarà uguale alla circonferenza del primo cerchio."
La dimostrazione non è cortissima e viene condotta con il metodo di esaustione di Archimede che era una specie di Excel dell'epoca.
Francesco Veneziano
Questa dimostrazione non ha niente a che vedere con quella di Archimede, e non
è per niente elegante, ma è il meglio che sia riuscito a fare sinora.
Indicherò con f’( x ) la derivata di f( x ) e con F( x ) la funzione inversa
a f( x )
Per derivare una funzione, è necessario che essa si presenti nella forma y=f(x)
Per una generica funzione in forma parametrica
x = f( t )
y = g( t )
si ha che
y = g( F(t) )
Sfruttando la formula della derivata composta abbiamo che
y’ = g’( F( t) )*F’( t )
sfruttando la formula per la derivata delle funzioni inverse si ha che
y’ = g’( F( t) )/f’( F( t) )
che si può ritrasformare in forma parametrica
x = f( t )
y = g’( t )/f’( t )
La spirale di Archimede è così espressa in forma parametrica:
x = kt cos t
y = kt sen t
dove t è l’angolo formato tra l’asse x e la retta che ruota generando la
spirale, e k è il rapporto tra la velocità radiale e quella angolare.
Questa spirale si svolge in senso antiorario partendo dal primo quadrante,
compirà un giro intersecando l’asse x e la tangente intersecherà il semiasse
negativo delle ordinate.
Sostituendo un angolo di 2p nell’equazione parametrica troviamo le coordinate
del punto in cui essa taglia l’asse (2kp ; 0)
La lunghezza della circonferenza di centro O e passante per (2kp ; 0) è 2p (
2kp ) = 4kp^2
Applicando la formula già trovata determiniamo l’equazione parametrica della
derivata della spirale
x = kt cos t
y = (sen t +t cos t) / (cos t - t sen t)
Sostituendo 2p a t troviamo il valore della derivata nel punto che ci interessa,
che è 2p
Possiamo ora trovare l’equazione della tangente alla spirale
y = 2p( x - 2kp )
Questa retta interseca l’asse y nel punto -4kp^2 la cui distanza dall’origine
è uguale alla lunghezza della circonferenza trovata precedentemente, QED
Pighin

![]()
178. Mai fidarsi dei numeri
proposto da Enrico Delfini
C’era una volta un professore di matematica che mangiava
sempre alla stessa trattoria; una trattoria alla buona, tant’è vero che al
momento del dolce non era possibile scegliere alla carta, ma ogni giorno veniva
offerto un solo tipo di dolce, tra Ananas, Budino e Crostata.
Il professore ogni giorno prendeva meticolosamente degli appunti misteriosi.
Il cameriere gli chiese spiegazione, e il professore spiegò: “Prendo nota del
gradimento che i vari dolci mi provocano, e ho scoperto che, attribuendo dei
valori di piacevolezza secondo un mio personale metodo, in una scala da 1 a 6,
il Budino mi piace sempre “3”, mentre l’Ananas a volte mi piace molto,”5”,
a volte solo “1”, la Crostata infine ottiene un gradimento molto vario, dal
”2” al “6”.
Possiamo immaginare tre meccanismi del tipo “ruota della fortuna” come questi: che esprimono le probabilità e i rispettivi punteggi per ogni portata.
|
A
1 (51%) |
B
3 (100%) |
C
2 (56%) |
Il cameriere, che non voleva passare per ignorante, andò in
cucina a fare due conti e tornò trionfante: “Professore, ho scoperto quale
dolce le piace di più!” e mostrò i suoi conti da cui risultava correttamente
che il gradimento atteso medio era di 2,96 per A, di 3 per B e di 3,32 per C.
“Ne risulta, se vogliamo usare il linguaggio di voi professori, che
(1) C > B > A
Passarono gli anni; la trattoria si ingrandì; ora, ogni giorno, la cucina
offriva la scelta, a rotazione, tra due delle tre portate.
Con sorpresa del cameriere, il cliente non ordinava secondo quanto previsto
dalla (1). “Se la scelta è tra A e B- spiegò il professore- è chiaro che B
mi darà un punteggio maggiore nel 51% dei casi; ma tra B e C, sarà B a darmi
il risultato migliore nel 56% dei casi, mentre C sarà meglio di A nel 61,78%
delle volte (il conto è facile da fare). Ne consegue che:
(2) B > C > A che è diversa da (1)
Il cameriere ci restò un po’ male, ma qualche giorno più tardi, pensò di
poter mettere in difficoltà il professore.
Era il compleanno del cuoco, e perciò, in via eccezionale, quel giorno, il menu
contemplava la scelta fra tutte e tre le portate. “Come la mettiamo oggi,
professore, facciamo valere la (1) e le porto la Crostata, o facciamo valere la
(2) e le porto il Budino?”
“Non sia mai - replicò il professore - se la scelta è fra tre, portami senz’altro
l’Ananas!”
E passò a dimostrare che, con tre scelte, B darà il risultato migliore solo se
contemporaneamente A dà 1 e C dà 2, cioè nel 51% del 56%, vale a dire nel
28,56%. C vincerà sempre col 6 (22%) e col 4 solo se A dà 1 (51% del 22%), per
un totale di 33,22%. Nel restante 38,22% dei casi prevarrà A.
Ne risulta
(3) A > C > B che è diversa sia da (1) che da (2)
A questo punto sapete rispondere alla semplice domanda: qual è il dolce
preferito dal professore?
Se siete in difficoltà, avete pienamente ragione. Dove è il trucco?
Nessun trucco; solamente non si è preventivamente stabilito quale significato
dare al concetto di “migliore”. Il bello (o il preoccupante) è che una
confusione di questo tipo siamo tutti portati a farla, anche in campi diversi.
Le implicazioni in campo medico sono decisamente sconcertanti, dal momento che
siamo tutti portati a considerare equivalente un buon risultato in termini di
durata di sopravvivenza media e un buon tasso di sopravvivenza a tot mesi o
anni. Immaginiamo per esempio di testare tre diversi trattamenti antitumorali;
se valuteremo la loro efficacia misurando separatamente la sopravvivenza media
dei pazienti trattati con le tre cure, ci troveremo nella situazione di (1), ma
se faremo uno studio di confronto valutando la sopravvivenza a tre, quattro o
cinque anni, avremo i risultati della (2) o della (3). E dovremo accettare che
la cura A, che risulta scientificamente la peggiore, se valutata da sola o in
confronto con una delle altre due, miracolosamente è quella che dà il miglior
risultato in un confronto a tre.
Invece che in campo medico, possiamo immaginare di avere a che fare con
produzioni agricole, o con rendimenti finanziari…
Possiamo anche aggiustare le cifre dei vari punteggi: abbassando i risultati di
A (per es. 0,2 e 4,2, il suo valore medio si riduce a un misero 2,16, ma il suo
piazzamento in (3) sarà sempre il migliore. Analogamente potremmo aumentare i
suoi punteggi (1,8 e 5,8) cosicché con una media di 3,76 sarebbe nettamente
primo in (1), pur restando ultimo in (2).
Quello che, a mio parere, sgomenta maggiormente, è il fatto di trovarci di
fronte a risposte ambigue, anche dopo aver affrontato il problema in maniera
aritmetica, affidandoci alla Scienza considerata la più esatta e imparziale di
tutte, appunto la Matematica.
Per restare nel campo delle scienze mediche, non c’è dubbio che è necessaria
una maggiore attenzione nella lettura ed interpretazione, anche inconscia, dei
dati della letteratura, fino ad un vero e proprio scetticismo costruttivo in cui
i risultati degli studi scientifici vengano filtrati attraverso il buon senso e
la pratica clinica.
P.S. Le soluzioni possibili sono due. Sapreste individuarle entrambe?
>>> Risposte &
riflessioni
Enrico Delfini
Se siete in difficoltà, avete pienamente ragione. Dove è il trucco?
Nessun trucco; solamente non si è preventivamente stabilito quale significato
dare al concetto di “migliore”. Il bello (o il preoccupante) è che una
confusione di questo tipo siamo tutti portati a farla, anche in campi diversi.
Le implicazioni in campo medico sono decisamente sconcertanti, dal momento che
siamo tutti portati a considerare equivalente un buon risultato in termini di
durata di sopravvivenza media e un buon tasso di sopravvivenza a tot mesi o
anni. Immaginiamo per esempio di testare tre diversi trattamenti antitumorali;
se valuteremo la loro efficacia misurando separatamente la sopravvivenza media
dei pazienti trattati con le tre cure, ci troveremo nella situazione di (1), ma
se faremo uno studio di confronto valutando la sopravvivenza a tre, quattro o
cinque anni, avremo i risultati della (2) o della (3). E dovremo accettare che
la cura A, che risulta scientificamente la peggiore, se valutata da sola o in
confronto con una delle altre due, miracolosamente è quella che dà il miglior
risultato in un confronto a tre.
Invece che in campo medico, possiamo immaginare di avere a che fare con
produzioni agricole, o con rendimenti finanziari…
Possiamo anche aggiustare le cifre dei vari punteggi: abbassando i risultati di
A (per es. 0,2 e 4,2, il suo valore medio si riduce a un misero 2,16, ma il suo
piazzamento in (3) sarà sempre il migliore. Analogamente potremmo aumentare i
suoi punteggi (1,8 e 5,8) cosicché con una media di 3,76 sarebbe nettamente
primo in (1), pur restando ultimo in (2).
Quello che, a mio parere, sgomenta maggiormente, è il fatto di trovarci di
fronte a risposte ambigue, anche dopo aver affrontato il problema in maniera
aritmetica, affidandoci alla Scienza considerata la più esatta e imparziale di
tutte, appunto la Matematica.
Per restare nel campo delle scienze mediche, non c’è dubbio che è necessaria
una maggiore attenzione nella lettura ed interpretazione, anche inconscia, dei
dati della letteratura, fino ad un vero e proprio scetticismo costruttivo in cui
i risultati degli studi scientifici vengano filtrati attraverso il buon senso e
la pratica clinica.
P.S. Le soluzioni possibili sono due. Sapreste individuarle entrambe?
![]()
177. Il terreno
proposto da Riccardo
Un proprietario lascia in eredità un terreno
rettangolare.
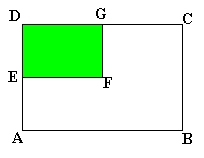
Nel testamento si legge: "Della mia proprietà A-B-C-D, con AB = 2 BC,
lascio al mio unico figlio la quarta parte E-F-G-D, come risulta dal
disegno; mentre i miei quattro nipoti dovranno dividersi il restante terreno in
quattro parti uguali per forma e dimensione."
P.S. Le soluzioni possibili sono due. Sapreste individuarle entrambe?
>>> Risposte &
riflessioni
Ringrazio (in ordine alfabetico, Andro,
Roberto Portaluri e Shylock le cui risposte sono arrivate quasi
contemporaneamente.
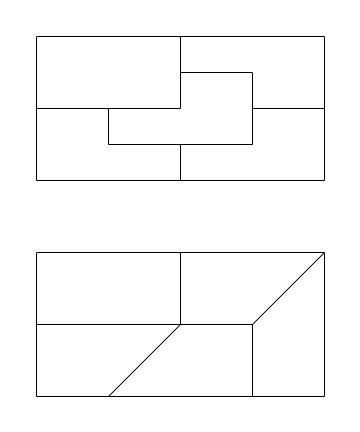
Ecco un mix delle soluzioni:
Una soluzione è la seguente: ogni pezzo è un trapezio rettangolo con basi una doppia dell'altra.
Di solito questo tipo di problemi si prova a risolverli, in prima istanza, suddividendo l’area in una quadrettatura nella quale il numero di caselle sia divisibile per il numero delle “zone” richieste.

![]()
176. Due 7 e due 2
proposto da Gianfranco Bo
Due 7 e due 2
(tratto dal newsgroup rec.puzzle)
Utilizzando due 7 e due 2 e le comuni operazioni e funzioni
matematiche (+, -, *, /, estrazione di radice, elevamento a potenza, fattoriale,
logaritmo, etc) è possibile ottenere diversi numeri, ad esempio:
15 = (7+7)+(2/2)
16 = sqrt(sqrt(2^(7+7+2)))
17 = (2+.7+.7)/.2
E' inoltre possibile utilizzare le notazioni:
E' possibile ottenere i numeri interi da 0 a 10?
E da 0 a 100?
Alcuni numeri non risolti: 82, 85
>>> Risposte &
riflessioni
Alessandro Torelli
85 = (7-2)! - (7/.2)
Grazie ad Alessandro per la soluzione tanto lapidaria quanto geniale.
Simone Stefanini
Se venisse concesso (il testo dice le più comuni funzioni matematiche)
l'utilizzo della funzione parte intera (indichiamola con "{}") l'82
verrebbe così espresso:
82= 77+ ({sqrt(2)} / .2)
Gianfranco Bo
Prendiamo atto della soluzione corretta di Simone.
Va notato che la "comunità" dei solutori di questo tipo di giochi
tende ad evitare l'utilizzo della funzione "parte intera" ed utilizza
raramente il log.
Però si tratta soltanto di regole convenzionali.
![]()
175. La Trasformazione-T
proposto da Gianfranco Bo
(Tratto da un problema non
completamente risolto su rec.puzzle)
Partiamo da una coppia di numeri naturali (a;b).
Possiamo applicare più volte una trasformazione (che chiamiamo Trasf-T) che
consiste in questo:
Ad esempio, dalla coppia (3;7) possiamo ottenere (4;14) oppure (6;8), a piacere.
Dimostrare che ogni coppia (a;b) può essere trasformata in una coppia di numeri uguali (x;x) mediante una sequenza opportuna di Trasf-T.
Ecco un esempio:
13 - 59
14 - 118
15 - 236
30 - 237
60 - 238
120 - 239
240 - 240
Un altro esempio:
1 - 2
2 - 3
4 - 4
>>> Risposte &
riflessioni
Gianfranco Bo
L'idea che sta alla base della dimostrazione è la seguente:
Per comodità adotto la seguente simbologia:
| a,b | |
| +R | a+1,2b |
| a,b | |
| R+ | 2a, b+1 |
n+R e nR+ indicano le precedenti trasformazioni ripetute n volte
Esempio:
| a,b | |
| n+R | a+n, 2nb |
| a,b | |
| nR+ | 2na, b+n |
Faccio un esempio numerico.
| inizio | 5,8 |
| 3+R | 8,64 |
| 2R+ | 32,66 |
| +R | 33,132 |
| 2R+ | 132,134 |
Come si vede, la differenza, inizialmente era 8-5 = 3 e, alla fine, dopo aver applicato 3+R, 2R+, +R, 2R+, abbiamo ottenuto 134-132=2: la differenza è diminuita di 1.
Detto questo, procediamo con la dimostrazione.
Partiamo dalla coppia:
a, a+d
Applichiamo d+R
a+d, 2d(a+d)
Scegliamo un numero n<d e applichiamo (d-n)R+
2d-n(a+d), 2d(a+d)
+ d - n
Applichiamo +R
2d-n(a+d)+1, 2d+1(a+d)
+ 2d - 2n
Applichiamo (n+1)R+
2n+12d-n(a+d)+2n+1,
2d+1(a+d) + 2d - 2n + n + 1
OK. Ora facciamo qualche calcolo.
2d+1(a+d)+2n+1, 2d+1(a+d) + 2d - n + 1
A noi interessa la differenza fra i due termini della coppia. Siccome non sappiamo qual è il maggiore, dobbiamo utilizzare il valore assoluto (uso il simbolo |x|).
2d+1(a+d)+2n+1- 2d+1(a+d) - 2d + n - 1
Due termini piuttosto pesantucci si eliminano.
differenza = |2n+1- 2d + n - 1|
Noi vorremmo che la differenza fosse minore di quella iniziale, che era d.
|2n+1- 2d + n - 1| < d
Ecco il nocciolo della questione. Visto che abbiamo SCELTO n, chiediamoci: per ogni d esiste qualche n che rende vera la disequazione?
Facciamo ancora qualche passaggio, eliminando il valore assoluto.
Ricordiamo che:
|x| > a per x > -a AND x < a
2n+1- 2d + n - 1 > -d
AND
2n+1- 2d + n - 1 < d
2n+1 + n > d + 1
AND
2n+1 + n < 3d + 1
Pongo n+1 = t
2t + t > d + 2
AND
2t + t < 3d + 2
La domanda finale, rappresentata sulla retta numerica, quindi è:
-------+-----------------+--------------------+-----------
......d+2.................2t +
t..................3d+2.......
Per ogni d >2 intero positivo esiste un t intero positivo tale che:
d+2 < 2t + t < 3d+2
Eulero, dove sei? Se ci sei batti un colpo!
Io comunque, credo di sì... ma questo deve ancora essere dimostrato.
W O W !
Andrea Becucci e Cesare Fattorosi di
Barnaba hanno trovato indipendentemente la soluzione. Si tratta di due
approcci diversi e molto interessanti al problema.
Le riporto in ordine di arrivo. Non sono proprio elementari e
immediate, per capirle ho dovuto meditarle molto attentamente. Vi consiglio di
fare altrettanto.
In rosso c'è la mia radiocronaca.
Andrea Becucci
Andrea inizia dicendo subito la
soluzione.
Per d = 1, 2 e 3 si cerca un t ad hoc.
Per d >= 4 si ha che:
t = parte intera del logaritmo in base 2 di 2(d+1)
ovvero
t = 1+parte intera del logaritmo in base 2 di (d+1)
Visto che siamo nei numeri interi,
d'ora in poi eviteremo di scrivere "parte intera di..."
t = log2 2(d+1) = log2 2 + log2 (d+1) = 1 + log2
(d+1)
Avremo perciò che 2t = 2(d+1) = 2d + 2
Fatte queste premesse la doppia diseguaglianza diventa (sostituendo):
d+2 < 2d+2+1 + log2 (d+1) < 3d+2
La prima diseguaglianza è vera per d>0
La seconda invece diventa:
2d+2+1 + log2 (d+1) < 3d+2
log2 (d+1) < d -1
d+1<2(d-1)
2(d+1)<2d
Può essere dimostrata graficamente
pensando alle funzioni
y = 2d + 2 (retta)
y = 2d (esponenziale)
o anche per induzione, come fa Andrea.
Questa va dimostrata per induzione.
Vale per d = 4
Si suppone che valga per d, ovvero 2d+2<2^d
Dimostriamo che vale per d+1, ovvero che 2(d+2)<2*(d+1) d+2<2^d
Dato che se d>0 d+2<2d+2 abbiamo d+2<2d+2<2^d
Cesare Fattorosi di Barnaba
Questo problema può essere ristretto a:
d+2< 2^t+t < 2(d+2) < 3d+2 per ogni d>2.
Rinominando le variabili, sempre considerate intere, tutto è piu'
leggibile.
Si pone x=d+2 e f(t)=2^t+t
per cui
x < f(t) <2x per ogni x>4
1 Considerazione
f(t)<f(t+1)<2f(t)
cioè il successivo 2^t+t che è 2^(t+1)+t+1 è minore di 2(2^t+t).
2t+1 + t + 1 < 2*2t + 2t = 2t+1 + 2t
Esempi:
per t=2 si ha 2^t+t=6
per t=3 si ha 2^t+t=11 <12 = al
doppio del precedente
per t=4 si ha 2^t+t=20
<22= al doppio del precedente
Dimostrazione per assurdo
supponiamo che non esista per ogni x un f(t) tale che
(a) x< f(t) <2x
allora sia
(b) f(j)=max{2^t+t}<x
allora
f(j+1)>x
(altrimenti sarebbe falsa per (b)),
f(j+1) dovrebbe anche essere maggiore di 2x (a)
ma f(j)<x implica (per la 1 Considerazione) f(j+1)<2f(j)<2x.
Per cui deve esistere.
facendo una tabella risulta tutto piu' chiaro. Tutto il trucco risiede nel fatto che il successivo 2^t+t è minore del suo doppio
d d+2 2^t+t 2(d+2)
3 5 6 10
4 6 11 20
5 7 11 14
6 8 11 16
7 9 11 18
8 10 11 20
9 11 20 22
Ritorniamo al problema base.
Ecco due strategie ad hoc per d = 1 e d = 2, le altre si possono sempre
risolvere con la procedura data all'inizio.
Per il caso d = 1 si ha:
PROCEDURA 1
a, a+1
a+1, 2a+2
a+2, 4a+4
2a+4, 4a+5
4a+8, 4a+6
La differenza ora è 2 e ricade nel caso d=2
Per il caso d = 2, si ha:
PROCEDURA 2
a, a+2
a+1,2a+4
a+2,4a+8
2a+4,4a+9
2a+5,8a+18
4a+10,8a+19
8a+20,8a+20
Applichiamo la procedura ad una coppia.
| inizio | 5,11 | d = 6 |
| 6+R | 11,704 | |
| 4R+ | 176,708 | tra 8 e 20 scelgo t=3 ovvero n=2 |
| +R | 177,1416 | |
| 3R+ | 1416,1419 | d = 3 |
| inizio | 1416,1419 | d = 3 |
| 3+R | 1419,11352 | |
| 2R+ | 5676,11354 | tra 5 e 11 scelgo t=2 ovvero n=1 |
| +R | 5677,22708 | |
| 2R+ | 22708,22709 | d=1 |
| PROC. 1 | 90840,90842 | d=2 |
| PROC. 2 | 726740,726740 | d=0 |
Sito Web realizzato da Gianfranco Bo