
[BASE Cinque - Appunti di Matematica ricreativa]
Una curva studiata per la (forse) prima volta da Galileo Galilei
Se sospendete una catena per gli estremi, purché non sia in direzione verticale, anche se la tendete con tutta la vostra forza, essa non sarà mai dritta.
Formerà sempre una curva, sotto l'azione della forza di gravità.

Catena a sfere.
Che curva è? Un arco di circonferenza? Una parabola?
Niente di tutto ciò: è una catenaria!
L'ho sentito dire e ci ho creduto, ma ora vorrei sperimentarlo.
Prima però, bisogna mettersi d'accordo su una questione: che cos'è una catena, o meglio una fune?
La fune è un oggetto cilindrico mooooooolto lungo (rispetto al suo raggio) che ha le seguenti proprietà meccaniche:
Una catena è più o meno come una fune con la differenza che invece di essere un pezzo unico è formata da tanti elementi uguali uniti uno di seguito all'altro. Tali elementi di solito sono anelli o sfere.
Per fare delle prove vi serve una catenella lunga circa 1 m e un semplice dispositivo con due aste verticali alle quali potete appendere la catenella per due suoi punti.
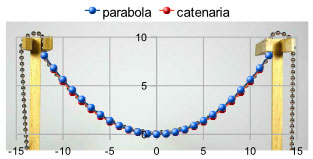
Nella figura qui sotto si vede la forma della catena appesa messa a confronto con una parabola (la linea con sfere blu).
Si vede chiaramente che la catenaria assomiglia alla parabola ma non è una parabola.
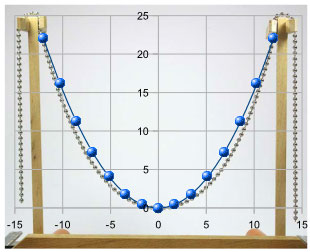
Attenzione: le palline blu NON indicano dei pesi ma i punti in cui è stata calcolata la parabola per disegnarne il grafico.
Se invece sovrapponete la catenella a una particolare funzione matematica, vedete che coincidono quasi perfettamente (linea con sfere rosse).
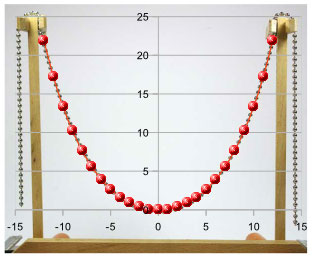
Attenzione: le palline rosse NON indicano dei pesi ma i punti in cui è stata calcolata la catenaria per disegnarne il grafico.
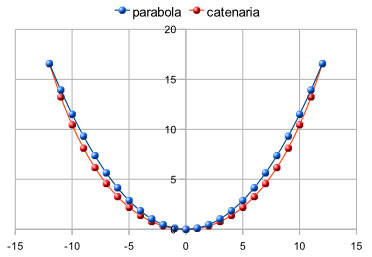
Qual è la formula della catenaria?
Difficile è ricavarla, ma semplice da vedersi:
y = a * cosh(x/a)
o meglio:
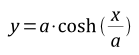
dove cosh = coseno iperbolico.
Se l'angolo formato dalla catenaria con la linea orizzontale che congiunge i punti di sospensione è minore di 45°, allora la parabola e la catenaria tendono a coincidere.
Alcune citazioni tratte da Galileo Galilei, Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze attenenti alla mecanica e i movimenti locali, 1638.
Giornata seconda. Salviati spiega come disegnare delle parabole.
"Salviati. Modi di disegnar tali linee ce ne son molti, ma due sopra tutti gli altri speditissimi glie ne dirò io: uno de i quali è veramente maraviglioso, poiché con esso, in manco tempo che col compasso altri disegnerà sottilmente sopra una carta quattro o sei cerchi di differenti grandezze, io posso disegnare trenta e quaranta linee paraboliche, non men giuste sottili e pulite delle circonferenze di essi cerchi. Io ho una palla di bronzo esquisitamente rotonda, non più grande d'una noce; questa, tirata sopra uno specchio di metallo, tenuto non eretto all'orizonte, ma alquanto inchinato, sì che la palla nel moto vi possa camminar sopra, calcandolo leggiermente nel muoversi, lascia una linea parabolica sottilissimamente e pulitissimamente descritta, e più larga e più stretta secondo che la proiezzione si sarà più o meno elevata. Dove anco abbiamo chiara e sensata esperienza, il moto de i proietti farsi per linee paraboliche: effetto non osservato prima che dal nostro amico, il quale ne arreca anco la dimostrazione nel suo libro del moto, che vedremo insieme nel primo congresso. La palla poi, per descrivere al modo detto le parabole, bisogna, con maneggiarla alquanto con la mano, scaldarla ed alquanto inumidirla, ché così lascerà più apparenti sopra lo specchio i suoi vestigii. L'altro modo, per disegnar la linea, che cerchiamo, sopra il prisma, procede così. Ferminsi ad alto due chiodi in un parete, equidistanti all'orizonte e tra di loro lontani il doppio della larghezza del rettangolo su 'l quale vogliamo notare la semiparabola, e da questi due chiodi penda una catenella sottile, e tanto lunga che la sua sacca si stenda quanta è la lunghezza del prisma: questa catenella si piega in figura parabolica, sì che andando punteggiando sopra 'l muro la strada che vi fa essa catenella, aremo descritta un'intera parabola, la quale con un perpendicolo, che penda dal mezo di quei due chiodi, si dividerà in parti eguali. Il trasferir poi tal linea sopra le faccie opposte del prisma non ha difficoltà nessuna, sì che ogni mediocre artefice lo saprà fare. Potrebbesi anco con l'aiuto delle linee geometriche segnate su 'l compasso del nostro amico, senz'altra fattura, andar su l'istessa faccia del prisma punteggiando la linea medesima."
Giornata quarta. Si parla di una somiglianza fra la traiettoria dei proiettili e la catenaria.
"Sagredo. (...) E l'accidente è l'esser impossibile distendere una corda sì, che resti tesa dirittamente e parallela all'orizonte; ma sempre fa sacca e si piega, né vi è forza che basti a tenderla rettamente. (...)"
" Salviati. (...) Ma più voglio dirvi, recandovi insieme maraviglia e diletto, che la corda così tesa, e poco o molto tirata, si piega in linee, le quali assai si avvicinano alle paraboliche: e la similitudine è tanta, che se voi segnerete in una superficie piana ed eretta all'orizonte una linea parabolica, e tenendola inversa, cioè col vertice in giù e con la base parallela all'orizonte, facendo pendere una catenella sostenuta nelle estremità della base della segnata parabola, vedrete, allentando più o meno la detta catenuzza, incurvarsi e adattarsi alla medesima parabola, e tale adattamento tanto più esser preciso, quanto la segnata parabola sarà men curva, cioè più distesa; sì che nelle parabole descritte con elevazioni sotto a i gr. 45, la catenella camina quasi ad unguem sopra la parabola."
Data creazione: luglio 2011
Ultimo aggiornamento: luglio 2011
xhtml 1.1
Sito Web realizzato da Gianfranco Bo