[HOME - BASE Cinque - Appunti di Matematica ricreativa]
come ottimizzare l'irrigazione di
un campo quadrato
Non si può fare a meno della
trigonometria e dell'analisi per risolvere questo problema?
Problema proposto al Forum da Enrico Delfini
Ho visto uno di quei grossi innaffiatori a
getto che irrigava un campo.
Mi sono avvicinato per curiosità, e per godermi una bella
doccia in questa calura, e ho potuto osservare che il getto
partiva da un palo posto al centro esatto di un un podere
perfettamente quadrato e che il getto era perfettamente
omogeneo lungo tutti i 360 gradi.
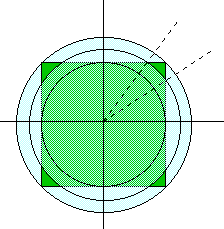
Il contadino mi ha spiegato che il campo misura 40x40 metri e
che il getto è regolabile fino ad una gittata massima di 28,284
metri.
"Il mio problema è che se regolo il getto a 20 metri mi
rimane asciutta una parte del campo ad ogni angolo; se metto
la potenza al massimo, innaffio gratuitamente un bel po'
dell'erba del vicino.
Quale gittata consente di minimizzare la somma (terreno mio
asciutto + terreno altrui bagnato)?

A parte la balistica, il succo della mia
domanda (pardon, del contadino!) è questo:
dato un quadrato di lato 40, qual è il raggio del cerchio (con
centro al centro del quadrato) che copre con la maggiore
efficienza il quadrato stesso; considerando come indice di
efficienza il cercare di minimizzare la somma delle aree
interne al quadrato non coperte (vicino ai vertici) e di
quelle esterne al quadrato coperte (a metà lato). Con raggio
20 il cerchio è tutto interno, ma rimane scoperta una area
vasta ad ogni angolo; con raggio 28,284 il quadrato è tutto
coperto, ma si copre anche molta superficie esterna...
Francesco Veneziano
La misura del campo è superflua, quindi possiamo supporre
che il lato del quadrato sia lungo 2; per sentirci più a
nostro agio fissiamo un riferimento cartesiano ortogonale con
origine nel centro del quadrato e assi paralleli ai lati del
campo. Per evidenti ragioni di simmetria possiamo limitarci
al solo primo quadrante, e consideriamo la circonferenza x^2+y^2=
r^2con1<=r<=sqrt2
A questo punto troviamo l'intersezione tra la circonferenza e
il quadrato (sqrt(r^2-1),1)
e scriviamo un po' di integrali, fino ad ottenere
un'espressione in r da minimizzare: (3/2)r^2arctg(sqrt(r^2-1))-(r^2/2)arcsin(1/r)-2sqrt(r^2-1)+1
Derivando e ponendo uguale a 0 devo risolvere
3arctg(sqrt(r^2-1))-arcsin(1/r)=0 cercando la soluzione tra 1
e sqrt2
Naturalmente non sono riuscito a risolvere questo mostro, ma
andando un po' "ad occhio" per tentativi ho stimato
che l'angolo tra l'origine e l'intersezione dovesse essere
circa un quarto di tutto il quardante, controllando questa
mia congettura con l'equazione si verifica che è corretta,
infatti ad un angolo di pi/8 corrisponde un raggio di sqrt(4-2sqrt2)
che effettivamente annulla la derivata (si verifica
laboriosamente con un po' ditrigonometria) e spreca 3-2sqrt2
di superficie, che va moltiplicata per 4 perchè ci eravamo
ristretti ad un solo quadrante.
In conclusione il raggio del cerchio deve essere sqrt(1-sqrt2/2)
= 0.5411961001 (circa) il lato del quadrato, e la superficie
spercata è 3-2sqrt2 = 0.1715728752 (circa) la superficie del
quadrato.
Ora vorrei sapere da Enrico se conosce qualche dimostrazione
di questo fatto che non sia la mia mostruosità analitica-trigoniometrica
e che non richieda mistici "mi accorgo che..." o
"andando ad occhio mi sembra che..."; mi
accontenterei anche di una dimostrazione pulita del fatto che
l'angolo che minimizza il tutto è pi/8.
Marco
Si circa e' giusto anche io un po' sperimentando ho
trovato quel valore, anche io son curioso della soluzioni
senza seni coseni tangenti e altre cose del genere.
Francesco Veneziano
In realtà non è strano che un problema
facile abbia una soluzione "difficile", anzi è
facilissimo (soprattutto in teoria dei numeri) produrre
problemi semplici e non risolubili con le tecniche attuali.
In geometria poi problemi "naturali" come la
quadratura del cerchio hanno richiesto secoli e un approccio
non geometrico per essere risolti.
A dire la verità io non avrei mai sperato di risolvere il
tuo problema se non fossi stato convinto (erroneamente)
dell'esistenza di una soluzione elementare; ho provato un po'
a caso solo perchè supponevo che il problema avesse una
soluzione semplice (come in effetti era) anche se di noiosa
dimostrazione.
Franco Cocca
Considerando per semplicità un quarto del campo da
innaffiare, posto l'idrante nel punto in basso a sinistra e
indicato con alpha l'angolo in figura:
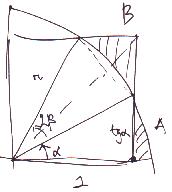
si ha che il raggio r= 1/cos(alpha).
La misura della superficie è:
A = r^2 alpha/2 - 1/2 tan(alpha) = alpha/(2 cos(alpha)^2)-1/2
tan(alpha).
La misura di B = 1-2*(1/2 tan(alpha)-r^2 (pi/2-2alpha)/2)=1-1/2
tan(alpha)-1/(2 cos)alpha)^2)(pi/2-2alpha)
A questo punto la funzione da minimizzare è 2A+B rispetto
alla variabile alpha.
Ebbene: 2A+B= 1-2 tan(alpha)+(8alpha-pi)/(4 cos(alpha)^2)
La derivata rispetto alla variabile alpha vale (8alpha-pi)
sin(alpha)/(2 cos(alpha)^3)
che si annulla proprio per alpha=pi/8
Pertanto il raggio che minimizza la somma delle aree vale:
1/cos(pi/8) = radq(4-2 radq(2)) =1.0824175
Sprmnt21
Mah ... non vorrei che quanto sto per scrivervi
rientri nella categoria delle visioni "mistiche",
ma mi pare che dal punto di vista geometrico il risultato di
Francesco sia autoevidente.
Naturalmente col senno di poi, una volta nota la soluzione(tra
l'altro la cosa che segue mi sembra la trasposizione
geometrica del ragionamento analitico di F).
Provo a descrivere le figure su cui faccio i ragionamenti al
meglio che posso (confido nella vostra comprensione).
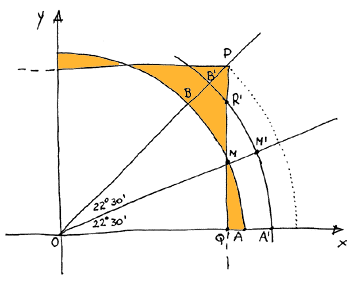
Mi metto nella situazione che ha introdotto F. Sia P il vertice del quadrato che sta nel primo quadrante, sia Q la proiezione di P sull'asse delle ascisse, sia M il punto tale che <QOM = pgreco/8 e siano A e B le intersezioni del cerchio di raggio OM con le rette OQ e OP rispettivamente.
Bisogna provare che la somma dei "triangoli" PBM
e QAM e' minima.
Infatti se M' e' un punto di OM tale che OP > OM' > OM
si ha che il cerchio di raggio OM' taglia PQ nel segmento MP
sia R' il punto in comune e siano A' e B' i punti in comune
con OQ e OP.
Per simmetria [AMM'A']=[BMM'B'] quindi [BMR'B']<[AMR'A'] cioe' la somma [PB'R']+[R'QA'] > [PBM]+[MQA] qualunque sia il punto M'.
In modo analogo si prova per un M" tale che OM"
< OM
che [PB"R"]+[R"QA"] > [PBM]+[MQA].
Siccome la cosa cosi' messa mi pare fin troppo semplice, mi
aspetto che ci sia qualche problema che mi sfugge e che
sicuramente non sfuggira a voi.
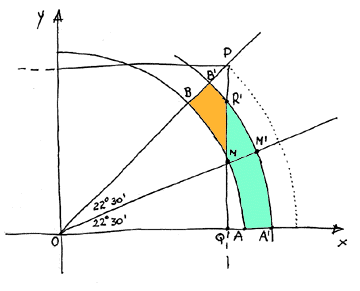
Il ragionamento di
Sprmnt21 in estrema sintesi:
per ogni M'<>M (nei limiti), la parte celeste è
maggiore della parte arancione
Sito Web realizzato da Gianfranco Bo