
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
detto anche principio della piccionaia
Ringrazio Sprmnt21, Giorgio Tumelero, Francesco Veneziano, Edmund, Bruno, Franco, Pietro Vitelli e Giobimbo per i notevoli contributi alla soluzione degli esercizi.
Introduzione
Esercizi di base
I cassetti di zio Erdos (esercizi
più difficili)
Nei suoi "Giochi di aritmetica e problemi interessanti", Giuseppe Peano presenta il seguente problema capzioso.
1. Sei letti per sette viaggiatori
Una comitiva di 7 viaggiatori si presenta ad un albergo, e domanda un letto per ogni viaggiatore.
L'oste risponde: "Ho solo sei letti distinti colle lettere A, B, C, D, E, F. Ma guarderò di aggiustarvi."
Perciò destinò:
Così i 7 viaggiatori dormono in 6 letti, uno per letto.
Come ha fatto?
Chi fa il gioco, rappresenta i letti con 6 carte e procede rapido, onde l'uditore non si accorga che un viaggiatore è stato contato due volte.
Questo gioco stupisce molto perché sembra dimostrare un fatto palesemente impossibile: che 7 persone possano dormire in 6 letti, una per letto.
L'impossibilità di fatti come questo viene espressa da un importante principio matematico: in inglese si chiama "pigeonhole principle", in italiano è stato tradotto con "principio della piccionaia", o "principio della cassettiera".
Pigeon = piccione o colombo domestico.
Pigeonhole = casella (o abitacolo in cui può stare un piccione).
Una piccionaia è una costruzione per il ricovero dei piccioni, costituita da un ambiente suddiviso in piccoli vani comunicanti con l'esterno per mezzo di piccole aperture quadrate.
In una piccionaia ci sono i quindi piccioni e le caselle. Ogni piccione ha la sua casella.
Il principio è chiamato anche Principio di Dirichlet perché
Gustave Peter Lejeune Dirichlet lo utilizzò nelle sue "Recherches sur
les formes quadratiques à coefficients et à indéterminées complexes"
per calcolare le approssimazioni razionali di numeri reali. Non gli diede subito
un nome. Solo in lavori successivi lo chiamò "Schubfach Prinzip".
| Il principio della piccionaia Il principio della piccionaia afferma che se p piccioni devono trovare posto in c caselle e ci sono più piccioni che caselle (p>c) allora in qualche casella entreranno almeno due piccioni. |
Esempio.
Se ci sono 8 piccioni in 7 caselle, allora, poiché 8 > 7, almeno una casella contiene almeno 2 piccioni.
Tale principio si può descrivere anche nel modo seguente.
|
Il principio della cassettiera |
Questo è un principio semplice ma di grande utilità. Infatti può aiutarci a risolvere problemi apparentemente molto complessi: basta individuare con un po' di arguzia cosa sono i piccioni e cosa sono le caselle.
| Estensione del principio della piccionaia Il principio della piccionaia può essere esteso così: Se p(iccioni) > n*c(aselle) per qualche intero n, allora almeno una casella contiene n + 1 piccioni. |
Esempio.
Se ci sono 27 piccioni in 8 caselle, allora, poiché 27 > 3*8, almeno una
casella contiene 3 + 1 = 4 piccioni.
Sempre nei "Giochi di aritmetica e problemi interessanti" di Giuseppe Peano si trova il seguente problema capzioso.
2. Due persone hanno lo stesso numero di capelli
Dimostrare che in una città di 150.000 abitanti vi sono due persone che hanno lo stesso numero di capelli.
Van Etten, 1624
Risposta
Peano precisa: si stima che la superficie del capo umano portante capelli è di 775 cm^2 e che ogni cm^2 contiene al massimo 165 capelli.
E conclude: il massimo numero che può avere una persona è 775 * 165 = 123.875 < 150.000.
Nota storica.
Le prime versioni di "Due persone hanno lo stesso numero di capelli" sono di van Etten, 1624, E. Fourrey, 1899 e dei logici di Port-Royal.
La domanda se in una grande foresta esistono alberi che hanno lo stesso numero di foglie si dice sia stata posta da Immanuel Kant (1724-1804) quando era un ragazzo.
Lietzmann dice che una quercia ha circa 2 milioni di foglie e un pino ha circa 10 milioni di aghi.
3. La biblioteca
In una grande biblioteca ci sono almeno due libri che contengono lo stesso numero di parole.
Abraham, 1933
4. Guanti e calzini in una stanza buia
Sei in una stanza buia e devi prendere dei guanti e dei calzini pescando a caso in due cassetti.
Perelman, FMP, 1935?
5. Palline nere, rosse e bianche
In un cassetto ci sono 12 palline nere, 8 rosse e 6 bianche.
Pescando a caso, quante se ne devono prendere per essere sicuri di averne 3 dello stesso colore?
H. Phillips, 1937
Il problema 24 degli esercizi di base è tratto dal libro Introductory Graph Theory di Gary Chartrand, 1985 (prima edizione del 1977 col titolo Graphs as Mathematical Models.
Si trova nel capitolo 2 e l'esercizio che lo precede chiede di dimostrare il Pigeonhole principle.
Ecco la citazione originale:


Gary Theodore Chartrand (n. 1936) ha numero di Erdos 1.
Il principio dei cassetti e le relazioni fra persone
1. Strette di mano
Ci sono 15 persone ad un party. Alcune di esse scambiano una stretta di mano con
altre.
Dimostrate che almeno due persone hanno stretto lo stesso numero di mani.
2. Amici
Dimostrate che in qualunque gruppo di 5 persone ce ne sono due che hanno lo
stesso numero di amici all'interno del gruppo.
3. Ancora amici
Considerate un gruppo di 50 persone. Alcuni sono amici e altri no.
Dimostrate che nel gruppo ci sono due persone che hanno lo stesso numero di
amici.
L'amicizia è una relazione simmetrica: se Aldo è amico di Ezio allora Ezio è
amico di Aldo.
Il principio dei cassetti e la teoria dei numeri
4. Somma pari
Dimostrate che dati tre numeri naturali, ce ne sono due la cui somma è pari.
5. Somma dispari
Dati 6 numeri interi compresi fra 1 e 10, almeno due hanno la somma dispari.
6. Somma data
Siano dati 27 numeri dispari minori di 100. Dimostrate che fra questi numeri
esiste una coppia la cui somma è 102
7. Somme uguali
Sia dato un insieme A di 10 numeri interi compresi fra 1 e 100.
All'interno di A si possono trovare due sottoinsiemi non vuoti S, T tali che la
somma degli elementi di S è uguale alla somma degli elementi di T.
L'unione di S e T non deve necessariamente essere uguale ad A.
8. Somma multipla
Dati 1000 interi, ne esistono almeno 2 la cui somma o la cui differenza è uguale
ad un multiplo di 1997.
9. Somma multipla di 5
In un qualunque gruppo di 17 numeri naturali se ne trovano 5 la cui somma è
divisibile per 5.
10. Somma divisibile per 5
Siano dati 5 numeri naturali a1, ... , a5
nessuno dei quali sia divisibile per 5.
Dimostrate che la somma di alcuni di essi (da 2 a 5) è divisibile per 5.
11. Somma divisibile per n
Siano dati n numeri naturali a1, ... , an.
Dimostrate che o uno di essi è divisibile per n o la somma di alcuni di essi (da
2 a n) è divisibile per n.
12. Differenza divisibile per 11
In un qualunque gruppo di 12 numeri naturali se ne trovano 2 la cui differenza è
divisibile per 11.
13. Differenza di potenze multipla
Esistono due potenze di 3 la cui differenza è divisibile per 1997?
14. Cifre terminali
Esiste una potenza di 3 che termina per 001?
15. Potenza multipla
Esistono due potenze di 2 la cui differenza è divisibile per 2001?
9. Diciannove con tre numeri
Tre numeri sono scelti a caso. La loro somma e' 19. Mostrare che almeno uno
numero e' maggiore od uguale a 7.
Il principio dei cassetti e la geometria
16. Sette dischi coprono un disco
Un disco di raggio 1 può essere completamente coperto con 7 dischi più piccoli,
identici fra loro. I dischi possono sovrapporsi parzialmente.
Qual è il raggio minimo che devono avere i dischi piccoli?
17. Alberi e distanze
Si ha un campo di 100 m di lato e si vuole piantare il massimo numero di alberi
in modo che la distanza fra qualunque coppia sia almeno 10 m. Quanti alberi si
dovranno piantare?
Si trascuri lo spessore dei tronchi.
18. Rettangolo con vertici dello stesso colore
Supponiamo che ciascun punto di un piano sia colorato di rosso o di blu.
I colori sono assegnati a caso, senza alcuna regolarità.
Dimostrare che esiste qualche rettangolo che ha tutti i vertici dello stesso
colore.
19. Vertici di un triangolo isoscele
Supponiamo che ciascun punto di una circonferenza sia colorato di rosso o di
blu.
I colori sono assegnati a caso, senza alcuna regolarità.
Dimostrare che esistono 3 tre punti dello stesso colore che sono i vertici di un
triangolo isoscele.
20. Punto medio in una griglia
Si scelgano 5 punti a caso sui nodi di una griglia a quadretti.
Esiste almeno un segmento che congiunge due punti tale che il suo punto medio si
trova su un nodo della griglia.
21. 51 punti in un quadrato
Si scelgano casualmente 51 punti all'interno di un quadrato di lato 1.
Dimostrare che in ogni caso 3 di questi punti possono essere coperti da un
cerchio di raggio 1/7.
22. Angolo minore di 26°
Tracciamo a caso 7 linee rette nel piano in modo che non ci siano rette
parallele.
Esistono 2 linee che formano un angolo minore di 26°?
23. Cinque punti in un triangolo
Provare che su 5 punti comunque scelti all'interno di un triangolo equilatero di
lato 1, ve ne sono almeno due che distano al piu' 1/2.

Il principio dei cassetti e i grafi
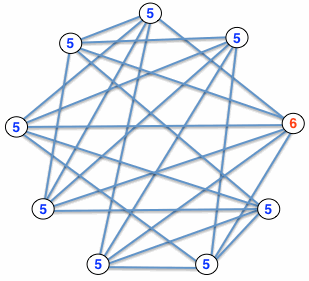
24. Grafo di 9 vertici
Un grafo è costituito da vertici e lati. I vertici sono generalmente
rappresentati con piccoli cerchi e i lati con linee che congiungono due vertici.
Il grado di un vertice è il numero di lati che partono (o terminano) da quel
vertice.
Considerate un grafo che ha 9 vertici e in cui ogni vertice ha grado 5 oppure 6.
Dimostrate che almeno 5 vertici hanno grado 6 oppure almeno 6 vertici hanno
grado 5.
Soluzione di Pietro Vitelli e Giobimbo (al Forum, maggio 2020)
Piccioni = i 9 vertici
Cassetti = le differenti tipologie di vertici (cassetto1 =
vertici di grado 6, cassetto 2 = vertici di grado 5).
Essendo 9 i vertici, e avendo 2 cassetti, è chiaro che uno dei due cassetti
conterrà sempre 5 o più elementi.
Ossia vi saranno sempre almeno 5 vertici di grado 6, oppure almeno 5 vertici di
grado 5.
Ci siamo quasi.
Ci basta dimostrare che il caso di 5 vertici di grado 5 non è possibile.
Vediamo.
Se avessimo 5 vertici di grado 5, avremmo i restanti 4 di grado 6.
Quindi avremmo come somma totale dei gradi dei vertici 5·5+4·6=49
Il che non è possibile perché sappiamo che tale somma deve essere pari.
Quindi scartando questo caso non possibile, vi saranno sempre almeno 5 vertici
di grado 6, oppure almeno 6 vertici di grado 5.
Altre applicazioni del principio dei cassetti
25. Utilizzo del computer
Un computer è stato utilizzato per 99 ore in un periodo di 12 giorni.
Dimostrare che esiste almeno una coppia di giorni consecutivi in cui il computer
è stato utilizzato almeno 17 ore.
26. Un milione di alberi
In una foresta ci sono un milione di alberi.
Ciascun albero ha non più di 600000 foglie.
Si dimostri che in ogni istante ci sono due alberi nella foresta che hanno lo
stesso numero di foglie.
27. Scatole numerate
Ci sono 10 scatole numerate da 1 a 10 nelle quali metteremo delle monete da 1
euro.
Quante monete sono necessarie per essere sicuri almeno una scatola contenga
almeno tante monete quanto è il suo numero?
28. Nove persone sedute in fila
Se 9 persone si siedono in una fila di 12 sedie, allora almeno 3 sedie
consecutive sono occupate.
29. Almeno un'aspirina al giorno
Una persona prende almeno una aspirina al giorno per 30 giorni.
Se prende in tutto 45 aspirine, allora esiste almeno una sequenza di giorni
consecutivi in cui ha preso esattamente 14 aspirine.
30. Matite colorate
Una scatola contiene 10 matite rosse, 8 blu, 8 verdi, 4 gialle.
Quante matite dovremo prendere, ad occhi chiusi, per essere sicuri di avere 4
matite dello stesso colore?
31. Somma di età
La somma delle età di un gruppo 33 persone è di 430 anni. E' vero che si può
trovare un sottogruppo di 20 persone la cui somma delle età è più di 260 anni?
32. Cinquecento cassette di mele
Ci sono 500 cassette di mele. Ciascuna cassetta contiene non più di x mele.
Si trovi il minimo (massimo?) valore di x tale che si possa essere sicuri che
esistano 3 cassette con lo stesso numero di mele.
33. Compleanni e giorni della settimana
Mostrare che in un gruppo di 8 persone almeno due hanno il loro compleanno nello
stesso giorno della settimana.
34. L'iniziale del nome
Mostrare che in un gruppo di 27 persone ce ne sono almeno due il cui nome
inizia con la stessa lettera.
35. Gli errori degli studenti
In una classe ci sono 30 studenti. Nel corso di un test uno studente ha fatto 12
errori, mentre il resto della classe ha fatto meglio. Mostra che almeno 3
studenti hanno fatto lo stesso numero di errori.
36. I libri nel cassetto
Un cassetto contiene 10 libri francesi, 20 spagnoli, 8 tedeschi, 15 russi e 25
italiani. Quanti ne dobbiamo prendere per essere sicuri di avere 12 libri nella
stessa lingua?
1. Cinque punti sul piano
Dati 5 punti qualunque su un piano tali che non ve ne siano tre allineati,
dimostrare che quattro di essi formeranno sempre un quadrilatero convesso.
Esther Klein, 1932
2. Nove punti sul piano
Dati 9 punti qualunque su un piano tali che non ve ne siano tre allineati,
dimostrare che cinque di essi formeranno sempre un pentagono convesso.
Endre Makai, c. 1932 (?)
3. Diciassette punti sul piano
Dati 17 punti qualunque su un piano tali che non ve ne siano tre allineati,
dimostrare che sei di essi formeranno sempre un esagono convesso.
(Non so se è stato dimostrato)
4. Il problema del lieto fine
Dati 2^(n-2) +1 punti qualunque su un piano tali che non ve ne siano tre
allineati, dimostrare che n di essi formeranno sempre un n-agono convesso.
P. Erdös & G. Szekeres, c. 1932 (?)
(Non so se è vero né se è stato dimostrato)
5. Sottosequenze
Ogni permutazione dei primi n^2-1 numeri interi positivi contiene una
sottosequenza crescente o decrescente di lunghezza n.
P. Erdös & G. Szekeres, 1935
6. Divisibile e divisore in una sequenza
Si scelgano n+1 interi fra i primi 2n. Ce n'è almeno uno divisibile per un'altro.
P. Erdös, 1937
3. La biblioteca
In una grande biblioteca ci sono almeno due libri che contengono lo stesso
numero di parole.
Abraham, 1933
Una riga di libro contiene al massimo 20 parole
Una pagina contiene al massimo 50 righe
Un libro contiene al massimo 1000 pagine.
In conclusione un libro contiene al massimo un milione di parole.
Se nella GRANDE BIBLIOTECA ci sono 1.000.001 libri di quel tipo allora almeno
due libri conterranno lo stesso numero di parole.
4. Guanti e calzini in una stanza buia
Sei in una stanza buia e devi prendere dei guanti e dei calzini pescando a caso
in due cassetti.
- In un cassetto ci sono 10 paia di calzini marroni e 10 paia blu. Quanti
calzini devi prendere per essere sicuro di avere un paio di calzini dello stesso
colore?
- In un cassetto ci sono 10 paia di guanti marroni e 10 blu. Quanti guanti devi
prendere per essere sicuro di avere un paio di guanti dello stesso colore?
Perelman, FMP, 1935?
Nel primo caso è sufficiente pescare 3 calzini.
Nel secondo caso occorre tener conto che i guanti destri sono diversi da quelli
sinistri.
Le possibilità colore-mano sono:
MD-MS-BD-BS
Io devo essere sicuro di avere un guanto destro e uno sinistro dello stesso
colore.
Nella peggiore delle ipotesi potrei pescare:
10 MD + 10BD (oppure S).
Ma al 21-esimo guanto sono sicuro che almeno un paio dello stesso colore c'è.
5. Palline nere, rosse e bianche
In un cassetto ci sono 12 palline nere, 8 rosse e 6 bianche.
Pescando a caso, quante se ne devono prendere per essere sicuri di averne 3
dello stesso colore?
H. Phillips, 1937
Nella peggiore delle ipotesi, 6 palline non sono sufficienti.
Infatti potrebbero essere B-B-N-N-R-R.
Supponiamo di essere arrivati a 6 palline senza averne 3 dello stesso colore.
Visto che i colori sono 3 e che la settima deve per forza essere B o N o R
allora se ne avranno almeno 3 dello stesso colore.
In conclusione bisogna pescarne almeno 7.
Il principio dei cassetti e le relazioni fra persone
1. Strette di mano
Ci sono 15 persone ad un party. Alcune di esse scambiano una stretta di mano con
altre.
Dimostrate che almeno due persone hanno stretto lo stesso numero di mani.
Soluzione di Pietro Vitelli
Dato che ci sono 15 persone al party, ciascuna persona può stringere un
numero di mani che va da 0 a 14, ovvero 15 configurazioni possibili.
Quindi potremmo pensare che ogni persona abbia una configurazione diversa (15
persone e 15 configurazioni possibili) ed in tal caso non ci sarebbero persone
che hanno stretto lo stesso numero di mani.
In realtà ci devo essere per forza due persone che hanno stretto lo stesso
numero di mani dato che non vi sono 15 configurazioni possibili;
infatti, se ad es., la persona 1 non ha stretto la mano con alcuno (ha stretto 0
mani), allora non vi può essere un' altra persona che ha stretto 14 mani, e cioè
che ha stretto la mano con tutti, perchè non può averla stretta con la persona
1, che non ha stretto la mano con alcuno.
Quindi è possibile una sola, delle configurazioni 0 e 14; per cui in totale
abbiamo 14 configurazioni possibili (in realtà, le configurazioni possibili sono
molto di meno, ma ciò già ci basta per dimostrare il problema);
dato che le persone sono 15, siamo certi che vi è una persona che ha una
configurazione uguale a quella di un'altra persona, e cioè che ha stretto lo
stesso numero di mani di un'altra persona.
2. Amici
Dimostrate che in qualunque gruppo di 5 persone ce ne sono due che hanno lo
stesso numero di amici all'interno del gruppo.
Soluzione di Pietro Vitelli
Qui, vale lo stesso discorso per le strette di mani, e cioè il principio dei
cassetti;
quindi, ogni persona del gruppo può avere da 0 a 4 amici; quindi 5
configurazioni possibili;
però, come sopra, le 5 persone del gruppo non possono avere 5 configurazioni
diverse;
infatti, ad es., se una persona del gruppo ha 0 amici, non ve ne può essere
un'altra del gruppo che ne ha 4.
Quindi vuol dire che ci sono almeno 2 persone del gruppo che hanno lo stesso
numero di amici.
3. Ancora amici
Considerate un gruppo di 50 persone. Alcuni sono amici e altri no.
Dimostrate che nel gruppo ci sono due persone che hanno lo stesso numero di
amici.
L'amicizia è una relazione simmetrica: se Aldo è amico di Ezio allora Ezio è
amico di Aldo.
Soluzione di Pietro Vitelli
In questo caso, ogni persona può avere da 0 a 49 amici; cioè 50
configurazioni possibili;
già, a priori, però, possiamo escludere che una persona abbia 49 amici (sia
amica con tutti), dato che il problema dice che nel gruppo vi sono anche persone
che non hanno amici (hanno 0 amici).
quindi, abbiamo 49 configurazioni possibili (come già detto per il problema 1,
le configurazioni sono molto di meno...);
dato che le persone del gruppo sono 50, vi devono essere almeno due persone che
hanno lo stesso numero di amici.
Il principio dei cassetti e la teoria dei numeri
4. Somma pari
Dimostrate che dati tre numeri naturali, ce ne sono due la cui somma è pari.
Soluzione di Pietro Vitelli
Sappiamo che la somma di due numeri è pari, se i due numeri sono entrambi
pari, o entrambi dispari.
Ora, dati 3 numeri naturali, ve ne devono per forza essere due pari o due
dispari, la cui somma è quindi pari.
Quindi, dati 3 numeri naturali, certamente ve ne sono due la cui somma è pari.
5. Somma dispari
Dati 6 numeri interi compresi fra 1 e 10, almeno due hanno la somma dispari.
Soluzione di Pietro Vitelli
Sappiamo che due numeri hanno somma dispari, se sono uno pari, e l'altro
dispari.
Quindi, dati 6 numeri naturali compresi tra 1 e 10, affinchè vi siano tra essi
due numeri la cui somma sia dispari, occorre che tra essi vi siano almeno un
numero pari ed uno dispari;
ora tra 1 e 10 possiamo scegliere al massimo 5 numeri tutti pari o 5 tutti
dispari;
poichè ne abbiamo 6, essi non possono essere tutti pari o tutti dispari, per cui
vi saranno almeno un numero pari ed uno dispari, e quindi vi saranno almeno due
numeri la cui somma è dispari.
6. Somma data
Siano dati 27 numeri dispari minori di 100. Dimostrate che fra questi numeri
esiste una coppia la cui somma è 102.
Soluzione di Pietro Vitelli
Innanzitutto notiamo che 102 = 51 + 51; chiaramente questa non è una coppia
valida perchè, i numeri devono essere diversi;
le coppie di numeri dispari inferiori a 100 che formano 102 sono: 49+53;
47+55;... fino a 3+99 (la coppia 101+1, non è valida, dato che i numeri dispari
scelti sono tutti inferiori a 100);
in totale, quindi le coppie di questi numeri che formano 102, sono 24, dato che
24 sono i numeri dispari compresi tra 51 e 100 (51 escluso) o che 24 sono i
numeri dispari compresi tra 1 e 50 (1 escluso);
tali coppie, in totale, sono formate da 48 numeri dispari tutti diversi e minori
di 100 (ossia tutti i numeri dispari minori di 100, escluso 1 e 51);
quindi, dati 27 numeri dispari minori di 100, mettendoci nel caso peggiore, è
cioè ammettendo di avere 1 e 51 (che non possono formare coppie valide) tra i 27
numeri, ne restano 25 dispari; dato che le coppie possibili sono 24, allora, tra
i 27 numeri iniziali vi è almeno una coppia di numeri la cui somma da 102.
7. Somme uguali
Sia dato un insieme A di 10 numeri interi compresi fra 1 e 100.
All'interno di A si possono trovare due sottoinsiemi non vuoti S, T tali che la
somma degli elementi di S è uguale alla somma degli elementi di T.
L'unione di S e T non deve necessariamente essere uguale ad A.
8. Somma multipla
Dati 1000 interi, ne esistono almeno 2 la cui somma o la cui differenza è uguale
ad un multiplo di 1997.
Soluzione di Pietro Vitelli
Mettiamoci nel caso peggiore;
quindi vogliamo prendere quanti più numeri possibili tali che la loro somma e la loro differenza non sia multipla di 1997;
consideriamo, dunque, un numero intero generico n; indichiamo con 1997*m il multiplo di 1997 immediatamente successivo ad n, e con 1997*(m-1) quello immediatamente precedente;
indichiamo con s1 la differenza tra 1997*m ed n (in pratica, la distanza di n da 1997*m) e con d1 la differenza tra n e 1997*(m-1).
Innanzitutto è chiaro che se ora prendiamo come altro numero s1, la somma di n ed s1 ci da un multiplo di 1997 (e cioè 1997*m);
se prendiamo d1 si ha: n-d1=1997*(m-1); lo stesso vale se scelgo numeri del tipo 1997*k+s1, con k=0,1,2,...,+inf, oppure del tipo 1997*k-d1; per cui, per la nostra condizione iniziale, non dobbiamo sceglierli;
Ciò, in pratica, significa che in ciascun intervallo dei numeri interi naturali, individuato da due multipli consecutivi di 1997, non dobbiamo scegliere, come numeri da inserire nel nostro insieme di 1000 interi, quelli che distano d1 dall'estremo inferiore dell'intervallo, e quelli che distano s1 dall'estremo superiore dell'intervallo.
Per cui, come secondo numero,dopo aver scelto n, prendiamo un numero p qualsiasi, appartenente ad uno di questi (infiniti) intervalli, che non disti d1 dall'estremo inferiore, e che non disti s1 dall'estremo superiore; chiamiamolo p;
Per cui siamo sicuri che la somma n+p o la differenza n-p non da un multiplo di 1997;
ora, analogamente a quanto detto per n, indichiamo con d2 la distanza di p dal multiplo di 1997 immediatamente precedente, e con s2 la distanza di p dal multiplo di 1997 immediatamente successivo; anche in questo caso, per non avere somma o differenza pari ad un multiplo di 1997, non dobbiamo scegliere numeri del tipo 1997*k+s2 o 1997*k-d2, con k=0,1,2,...,+inf;
per cui, a questo punto, in ciascun intervallo di numeri interi naturali, individuato da due multipli consecutivi di 1997, non dobbiamo scegliere i numeri che distano d1 e d2 dall'estremo inferiore, e s1 e s2 da quello superiore.
Per cui, ricapitolando, dopo aver scelto 1 numero intero, già non potevamo scegliere 2 numeri interi in ciascun intervallo individuato da multipli consecutivi di 1997.
Ora, dopo aver scelto 2 numeri interi, non possiamo scegliere 4 numeri in ciascun intervallo;
è chiaro che, andando avanti, per ogni numero scelto, avremo un numero doppio di numeri che non possiamo scegliere;
in particolare, dopo aver scelto il 999° numero intero, avremo che, per evitare che due numeri tra i nostri interi scelti, abbiano somma o differenza pari ad un multiplo di 1997, non possiamo scegliere il doppio di 999, e cioè 1998 numeri di ciascun intervallo individuato da multipli consecutivi di 1997;
ma in ciascun intervallo, comprensivo di un solo estremo, ci sono proprio 1998 numeri; ciò significa che, scegliendo il 1000° numero intero, avremo sicuramente due numeri dei 1000 scelti (tra cui proprio questo 1000° numero) la cui somma o differenza è proprio un multiplo di 1997.
Per cui, nel caso peggiore, possiamo scegliere al massimo 999 numeri tali che la somma o la differenza di due di essi non sia un multiplo di 1997.
Quindi, in un insieme di 1000 interi, ve ne sono sicuramente 2 la cui somma o differenza è un multiplo di 1997.
9. Somma multipla di 5
In un qualunque gruppo di 17 numeri naturali se ne trovano 5 la cui somma è
divisibile per 5.
10. Somma divisibile per 5
Siano dati 5 numeri naturali a1, ... , a5
nessuno dei quali sia divisibile per 5.
Dimostrate che la somma di alcuni di essi (da 2 a 5) è divisibile per 5.
11. Somma divisibile per n
Siano dati n numeri naturali a1, ... , an.
Dimostrate che o uno di essi è divisibile per n o la somma di alcuni di essi (da
2 a n) è divisibile per n.
12. Differenza divisibile per 11
Soluzione di Pietro Vitelli
In un qualunque gruppo di 12 numeri naturali se ne trovano 2 la cui differenza è divisibile per 11.
Si nota che la differenza di due numeri naturali del tipo, ad es., 1+11k, è sempre divisibile per 11;
infatti (1+11k)-(1+11k')=11(k-k'), che è divisibile per 11.
Lo stesso vale per i numeri del tipo
0+11k
1+11k
2+11k
...
...
10+11k
ossia vale per tutte le classi di resto modulo 11.
Quindi per avere 12 numeri naturali la cui differenza non sia divisibile per 11, dovremmo avere 12 numeri appartenenti ognuno ad una classe di resto modulo 11 diversa;
siccome, però, le classi di resto modulo 11 sono esattamente 11, vuol dire che vi saranno obbligatoriamente due numeri che farannno parte della stessa classe di resto modulo 11, ossia la cui differenza sia divisibile per 11.
13. Differenza di potenze multipla
Esistono due potenze di 3 la cui differenza è divisibile per 1997?
14. Cifre terminali
Esiste una potenza di 3 che termina per 001?
Soluzione di Edmund
la più piccola è 3^100:
3^100 = 515377520732011331036461129765621272702107522001
in generale sono del tipo 3^(n*100) con "n" numero naturale
in quanto qualunque potenza di 3^100 terminerà sempre per 001
(Riporto le seguenti soluzioni sotto forma di immagini gif perché contengono molte gormule)
Soluzione di Pietro Vitelli

Soluzione di Bruno

15. Potenza multipla
Esistono due potenze di 2 la cui differenza è divisibile per 2001?
9. Diciannove con tre numeri
Tre numeri sono scelti a caso. La loro somma e' 19. Mostrare che almeno uno
numero e' maggiore od uguale a 7.
Risposta
I tre numeri sono le caselle mentre i piccioni sono 19.
Praticamente suppongo che i numeri siano interi positivi e che ogni piccione sia
una unità. Questi 19 piccioni si dividono in tre gruppi e vanno ad occupare le 3
caselle.
Poiché 19 > 6*3 allora almeno una casella contiene 6+1 = 7 piccioni (il numero
7)
Il principio dei cassetti e la geometria
17. Sette dischi coprono un disco
Un disco di raggio 1 può essere completamente coperto con 7 dischi più piccoli,
identici fra loro. I dischi possono sovrapporsi parzialmente.
Qual è il raggio minimo che devono avere i dischi piccoli?
18. Alberi e distanze
Si ha un campo di 100 m di lato e si vuole piantare il massimo numero di alberi
in modo che la distanza fra qualunque coppia sia almeno 10 m. Quanti alberi si
dovranno piantare?
Si trascuri lo spessore dei tronchi.
18. Rettangolo con vertici dello stesso colore
Supponiamo che ciascun punto di un piano sia colorato di rosso o di blu.
I colori sono assegnati a caso, senza alcuna regolarità.
Dimostrare che esiste qualche rettangolo che ha tutti i vertici dello stesso
colore.
19. Vertici di un triangolo isoscele
Supponiamo che ciascun punto di una circonferenza sia colorato di rosso o di
blu.
I colori sono assegnati a caso, senza alcuna regolarità.
Dimostrare che esistono 3 tre punti dello stesso colore che sono i vertici di un
triangolo equilatero.
20. Punto medio in una griglia
Si scelgano 5 punti a caso sui nodi di una griglia a quadretti.
Esiste almeno un segmento che congiunge due punti tale che il suo punto medio si
trova su un nodo della griglia.
21. 51 punti in un quadrato
Si scelgano casualmente 51 punti all'interno di un quadrato di lato 1.
Dimostrare che in ogni caso 3 di questi punti possono essere coperti da un
cerchio di raggio 1/7.
22. Angolo minore di 26°
Tracciamo a caso 7 linee rette nel piano in modo che non ci siano rette
parallele.
Esistono 2 linee che formano un angolo minore di 26°?
Soluzione di Pietro Vitelli
Sicuramente esiste un angolo minore di 26°.
Per dimostrarlo mettiamoci, come sempre, nel caso peggiore.
Consideriamo le prime due rette;
il caso peggiore è che il minore degli angoli che si vengono a formare dal loro incrocio sia massimo; per cui il caso peggiore è che le due rette siano ortogonali e quindi l'angolo d'incrocio è 90°.
A questo punto, nel tracciare le altre rette possiamo tener conto del fatto che rette parallele tagliate da una o più trasversali, generano, con la stessa trasversale, gli stessi angoli.
Per cui, per maggiore semplicità, facciamo passare tutte le rette, dalla 3° alla 7°, nel punto di incrocio delle prime due.
Ora, nel caso peggiore, la 3° retta formerà un angolo di 26° con una delle prime due rette;
la 4° retta la consideriamo ortogonale alla 3°, in modo da far rimanere invariati gli angoli (vedi figura successiva).
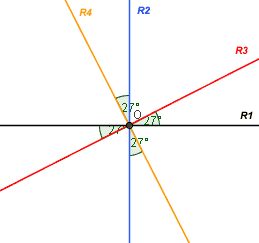
*gli angoli in figura sono di 26° e non di 27°
Procedendo allo stesso modo, tracciamo la 5° retta, in modo che formi con la 3° retta, inserita in precedenza, un angolo di 26°; con la 2° retta formerà un angolo di 90-26-26=38° (vedi figura in basso);
la 6° la tracciamo ortogonale alla 5°; per cui:
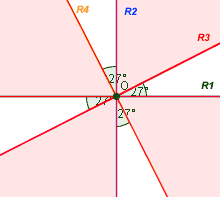
*gli angoli in figura sono di 26° e 38°, e non di 27° e 36°
Si nota che lo spazio restante (quello in rosso nella figura) per inserire la 7° retta è "ampio" 36°; per cui, comunque la tracciamo all'interno di tale spazio otterremo sempre un angolo minore di 26°
23. Cinque punti in un triangolo
Provare che su 5 punti comunque scelti all'interno di un triangolo equilatero di
lato 1, ve ne sono almeno due che distano al piu' 1/2.

Il principio dei cassetti e i grafi
24. Grafo di 9 vertici
Un grafo è costituito da vertici e lati. I vertici sono generalmente
rappresentati con piccoli cerchi e i lati con linee che congiungono due vertici.
Il grado di un vertice è il numero di lati che partono (o terminano) da quel
vertice.
Considerate un grafo che ha 9 vertici e in cui ogni vertice ha grado 5 oppure 6.
Dimostrate che almeno 5 vertici hanno grado 6 oppure almeno 6 vertici hanno
grado 5.
Altre applicazioni del principio dei cassetti
25. Utilizzo del computer
Un computer è stato utilizzato per 99 ore in un periodo di 12 giorni.
Dimostrare che esiste almeno una coppia di giorni consecutivi in cui il computer
è stato utilizzato almeno 17 ore.
26. Un milione di alberi
In una foresta ci sono un milione di alberi.
Ciascun albero ha non più di 600000 foglie.
Si dimostri che in ogni istante ci sono due alberi nella foresta che hanno lo
stesso numero di foglie.
27. Scatole numerate
Soluzione di Pietro Vitelli
Ci sono 10 scatole numerate da 1 a 10 nelle quali metteremo delle monete da 1
euro.
Quante monete sono necessarie per essere sicuri almeno una scatola contenga
almeno tante monete quanto è il suo numero?
Per avere la sicurezza che almeno una scatola contenga almeno tante monete quant'è il suo numero, dobbiamo metterci nel caso peggiore.
Il caso peggiore si ha quando in ogni scatola abbiamo messo un numero di monete pari al numero di etichetta della scatola meno 1.
Per cui nella 1° scatola abbiamo 0 monete, nella 2° una, nella 3° due, e così via fino alla 10° in cui ce ne sono 9;
per un totale di 1+2+3+4+5+6+7+8+9=45.
Per cui può capitare, (nel caso peggiore appunto) di aver inserito 45 monete complessive nelle scatole, ed ancora non vi è almeno una scatola che contenga almeno un numero di monete quanto è il suo numero.
A questo punto, in qualsiasi scatola inseriamo un'altra moneta, quella scatola conterrà sicuramente almeno tante monete quant'è il suo numero.
Quindi sono necessarie 46 monete per essere sicuri che almeno 1 scatola contenga almeno tante monete quant'è il suo numero.
28. Nove persone sedute in fila
Se 9 persone si siedono in una fila di 12 sedie, allora almeno 3 sedie
consecutive sono occupate.
Soluzione di Pietro Vitelli
Proviamo a far sedere quante più persone possibili senza che vi siano 3 sedie consecutive occupate.
Nel caso migliore, possiamo far sedere le persone 2 sedie si ed 1 no; per un totale di 8 persone sedute; a questo punto, se la nona persona si siede in una qualsiasi delle sedie vuote, si avranno sempre 3 sedie consecutive occupate.
29. Almeno un'aspirina al giorno
Una persona prende almeno una aspirina al giorno per 30 giorni.
Se prende in tutto 45 aspirine, allora esiste almeno una sequenza di giorni
consecutivi in cui ha preso esattamente 14 aspirine.
30. Matite colorate
Una scatola contiene 10 matite rosse, 8 blu, 8 verdi, 4 gialle.
Quante matite dovremo prendere, ad occhi chiusi, per essere sicuri di avere 4
matite dello stesso colore?
31. Somma di età
La somma delle età di un gruppo 33 persone è di 430 anni. E' vero che si può
trovare un sottogruppo di 20 persone la cui somma delle età è più di 260 anni?
Soluzione di Pietro Vitelli
Si, è vero.
Per dimostrarlo dobbiamo metterci nel caso peggiore; il caso peggiore si ha considerando tra tutte le possibili combinazioni di età la cui somma fa 430 anni, quella in cui l'età massima è la minima tra tutte le età massime delle altre combinazioni.
Tale combinazione peggiore la calcoliamo effettuando la divisione 430/33 = 13.0303... che approssimato per eccesso all'intero più vicino è 14.
Quindi nel caso peggiore si ha
13 + 13 + ... + 13 + 14 = 13 x 32 + 14 = 430
In questa combinazione, che è il caso peggiore (e cioè il caso in cui si ha il minor numero di sottogruppi di 20 persone con somma di età > 260 anni), si nota che vi è almeno un sottogruppo di 20 persone la cui somma di età è > 260 anni;
Infatti
13 x 19 + 14 = 261
Quindi, in un gruppo di 33 persone la cui somma delle età è 430, si può sempre trovare un sottogruppo di 20 persone la cui somma delle età è > 260 anni.
32. Cinquecento cassette di mele
Ci sono 500 cassette di mele. Ciascuna cassetta contiene non più di x mele.
Si trovi il minimo (massimo?) valore di x tale che si possa essere sicuri che
esistano 3 cassette con lo stesso numero di mele.
Soluzione di Franco
Rovistando nei meandri del forum (ci bazzico da poco tempo ed ho ancora tanto da scoprire), ho trovato questo quesito dalla risposta apparentemente semplice che però non mi convince del tutto:
La risposta esatta credo dovrebbe essere x=249 :
1^ = 0
2^ = 0
3^ = 1
4^ = 1
...
496^ = 247
497^ = 248
498^ = 248
e sia la 499^ che la 500^ cassetta non potranno che replicare una delle quantità già contenute nelle precedenti.
33. Compleanni e giorni della settimana
Mostrare che in un gruppo di 8 persone almeno due hanno il loro compleanno nello
stesso giorno della settimana.
Risposta
Naturalmente il problema è riferito ad un dato anno in quanto il giorno della
settimana del compleanno cambia di anno in anno.
Le persone sono i piccioni e i giorni della settimana sono le caselle.
Siccome 8>7 vale la tesi.
Senza utilizzare direttamente il principio della piccionaia, avremmo dovuto
ragionare così:
Nella più ampia situazione il gruppo potrebbe essere formato da:
a) una persona che compie gli anni di LUN, e contiamo 1.
b) una persona che compie gli anni il MAR, e fanno 2
c) una persona che compie gli anni il MER, e fanno 3
d) una persona che compie gli anni il GIO, e fanno 4
e) una persona che compie gli anni il VEN, e fanno 5
f) una persona che compie gli anni il SAB, e fanno 6
g) una persona che compie gli anni la DOM, e fanno 7
L'ottava persona deve necessariamente compiere gli anni in uno dei giorni
già citati perciò, in questo caso esisteranno 2 persone che compiono gli anni
nello stesso giorno della settimana.
Ma questo è il "caso peggiore", perciò la tesi vale anche per gli altri casi.
34. L'iniziale del nome
Mostrare che in un gruppo di 27 persone ce ne sono almeno due il cui nome
inizia con la stessa lettera.
Risposta
I nomi (27) sono i piccioni e le lettere dell'alfabeto sono le caselle.
Siccome 27>26 vale la tesi.
35. Gli errori degli studenti
In una classe ci sono 30 studenti. Nel corso di un test uno studente ha fatto 12
errori, mentre il resto della classe ha fatto meglio. Mostra che almeno 3
studenti hanno fatto lo stesso numero di errori.
Risposta
Gli studenti (30) sono i piccioni e i numeri di errori (da 0 a 12) le caselle:
30 piccioni in 12 caselle.
Poiché 30 > 2*12 allora almeno 2+1 = 3 studenti hanno fatto lo stesso numero di
errori.
In altre parole: con 30 piccioni, nella peggiore delle ipotesi, riempio tutte le
12 caselle, e poi le riempio di nuovo e poi mi avanzano ancora 6 piccioni: in
qualcuna ce ne dovranno stare almeno 3! Dài!
36. I libri nel cassetto
Un cassetto contiene 10 libri francesi, 20 spagnoli, 8 tedeschi, 15 russi e 25
italiani. Quanti ne dobbiamo prendere per essere sicuri di avere 12 libri nella
stessa lingua?
Risposta
Vorrei fare un altro ragionamento: quello della peggiore ipotesi.
Se prendo 10 libri, potrebbero essere tutti francesi.
Se prendo 10 + 8 libri, potrebbero essere tutti quelli francesi e tedeschi.
Se prendo più di 18 libri e qualcuno mi ha dato il malocchio, prendo tutti
quelli francesi e tedeschi, e in egual misura delle altre lingue.
Per essere sicuro di averne almeno 12 della stessa lingua ne devo prendere: 10 +
8 + 11 + 11 + 11 + 1 = 52
1. Cinque punti sul piano
Dati 5 punti qualunque su un piano tali che non ve ne siano tre allineati,
dimostrare che quattro di essi formeranno sempre un quadrilatero convesso.
Esther Klein, 1932
???
2. Nove punti sul piano
Dati 9 punti qualunque su un piano tali che non ve ne siano tre allineati,
dimostrare che cinque di essi formeranno sempre un pentagono convesso.
Endre Makai, c. 1932 (?)
???
3. Diciassette punti sul piano
Dati 17 punti qualunque su un piano tali che non ve ne siano tre allineati,
dimostrare che sei di essi formeranno sempre un esagono convesso.
(Non so se è stato dimostrato)
???
4. Il problema del lieto fine
Dati 2^(n-2) +1 punti qualunque su un piano tali che non ve ne siano tre
allineati, dimostrare che n di essi formeranno sempre un n-agono convesso.
P. Erdös & G. Szekeres, c. 1932 (?)
(Non so se è vero né se è stato dimostrato)
???
5. Sottosequenze
Dimostrare che, tra gli n^2+1 numeri di una generica sequenza, e' sempre
possibile trovarne n+1 successivi, ordinati in modo crescente o decrescente.
P. Erdös & G. Szekeres, 1935
Soluzione inviata da Sprmnt21
Per ogni numero, si costruisca la successione crescente piu' lunga
possibile, ottenendo:
a1 = A1_1 < A1_2 < ... < A1_h1
a2 = A2_1 < A2_2 < ... < A2_h2
.
.
.
aj = Aj_1 < Aj_2 < ... < Aj_hj
.
.
.
ak = Ak_1 < Ak_2 < ... <Ak_hk
dove k = n^2+1.
Se, per qualche j, n < hj allora non c'e' piu' nulla da provare.
Se hj =< n per j = 1,2, ..., k, allora esistono n+1 indici j(1) < j(2) < ... <
j(n+1) per cui: (*) hj(1) = hj(2) = ... = hj(n+1).
Per questi indici, si ha necessariamente che aj(1) > aj(2) > ... > aj(n+1).
Infatti se, per assurdo, aj(s) > aj(r) per j(s) > j(r), si avrebbe che hj(r) <
hj(s) [infatti, in questo caso, alla serie, lunga hj(s), che comincia con aj(s)
si potrebbe pre-appendere almeno l'elemento aj(r)] contraddicendo la (*).
6. Divisibile e divisore in una sequenza
Si scelgano n+1 interi fra i primi 2n. Ce n'è almeno uno divisibile per un'altro.
P. Erdös, 1937
Dimostrazione inviata da Sprmnt21
Nel testo ho usato:
U per indicare l'unione fra insiemi;
C per indicare "contenuto in";
#H per indicare la cardinalità dell'insieme H, cioè il numero dei suoi elementi;
il resto dei simboli dovrebbe essere autoesplicativo.
Sia N={1, 2, ..., n, n+1, n+2, ..., 2n} l'insieme da cui scegliere n+1 elementi.
Consideriamo la seguente partizione di N/{1}:
N=H1 U H2 U H3 U... U Hk, dove:
H1={2n, 2n-1, ..., n+1},
H2={n, n-1,..., [n/2]+1},
H3={[n/2], [n/2]-1, ..., [n/4]+1},
...,
Hk={[n/2^(k-2)] ,..., [n/2^(k-1)]+1}.
| Ad esempio, se: N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28} abbiamo: |
|
| H1 = | {15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28} |
| H2 = | {8, 9, 10, 11, 12, 13, 14} |
| H3 = | {4, 5, 6, 7} |
| H4 = | {2, 3} |
Per come sono stati costruiti, gli insiemi Hi godono della proprieta' che il
"doppio" di Hp e' contenuto in H(p-1), il "quadruplo" in H(p-2), e cosi via.
Per "doppio" di Hp={e1, e2, ..., ep} si intende l'insieme DHp contenente i
numeri {2e1, 2e2, ..., e2p}.
| Gianfranco Bo Prima di proseguire con la dimostrazione di Sprmnt21, desidero illustrarne il senso dal punto di vista intuitivo, senza entrare nei dettagli tecnici. Per la spiegazione mi riferirò all'insieme N = {1, ..., 28} Dobbiamo dimostrare che comunque prendiamo 14+1=15 interi nell'insieme, ve ne sarà almeno 1 divisibile per un altro. Chiamiamo S questo insieme di 15 elementi I 15 numeri sono i piccioni ma si può dimostrare che esistono al massimo 14 caselle per contenerli. E' chiaro che se in S vi è il numero 1 allora tutti gli altri sono
suoi multipli e il teorema, in questo caso, vale. Se per caso accade che abbiamo preso più di 4 numeri appartenenti a
H3 U H4 allora, per il principio della piccionaia, almeno uno è multiplo
di un altro. Ed il teorema, in questo caso, vale. Supponiamo di aver preso elementi solo da H3 in su. E supponiamo di
aver preso non più di 7 elementi tra H3 e H2. E supponiamo ancora che
nessun elemento sia multiplo di un altro. Questa si chiama "peggiore
delle ipotesi". Ora c'è un punto cruciale: il "trasporto" su H2. Costruiamo un nuovo
insieme S' sostituendo al posto di 5, 6 rispettivamente 10, 12. In
questo modo S' sta tutto su H2. Per completare l'opera devo ancora prendere 9 elementi in H1. |
Altri esempi:
Se N={1, 2, ..., 10, 11, 12, ..., 20}, abbiamo:
N/{1}={20, 19, ...,11} U {10, ..., 6} U {5, ..., 3} U {2}.
Se N={1, 2, ..., 15, 16, 17, ..., 32}, abbiamo:
N/{1}={32, 11, ...,17} U {16, ..., 9} U {8, ..., 5} U {4,3} U {2}.
Analizziamo ora un generico sottoinsieme di N di n+1 elementi che indichiamo
con S.
Dato che H1 ha n elementi S deve avere almeno un elemento di H1, siano h1>=1 gli
elementi comuni ad S ed H1.
In generale indichiamo con hi il numero di elementi di S contenuti in Hi, con
alcuni hi eventualmente nulli.
Per ipotesi h1+h2+...+hk=n+1.
Sia r il piu grande (*) indice per cui hr=/=0.
Se hr+h(r-1) > #H(r-1), dato che DHr C H(r-1), qualcuno degli h(r-1) elementi di H(r-1) e' un multiplo di qualcuno degli hr elementi di Hr e pertanto non c'e piu' nulla da provare.
Se, invece, hr+h(r-1) =< #H(r-1) e, per caso, nessuno degli h(r-1) elementi
di H(r-1) e' multiplo di alcuno degli hr elementi di Hr allora possiamo
immaginare di sostituire gli hr elementi con i corrispondenti "doppi" di H(r-1)
che avra' a questo punto h'(r-1)=hr+h(r-1) elementi.
Procedendo in questo modo, se non giungiamo prima ad una situazione con degli
elementi multipli fra loro, arriveremo ad avere:
h'2 = h2+h3+h4+...+hk elementi in H2.
Ma a questo punto avremo:
n+1=h'2+h1 > #H1 = n
e quindi almeno una coppia di elementi (uno degli h'2 e uno degli h1) saranno
uno multiplo dell'altro.
In effetti l'espressione, piu' volte usata, " uno multiplo dell'altro" puo'
essere specificata, per come ho costruito la partizione, affermando che e' "uno
degli elementi di H(i-1) ad essere eventualmente multiplo di uno degli elementi
di Hi".
Un'altra cosa da aggiungere e' la spiegazione del perche' ho escluso l'1 dalla
partizione di N negli Hi.
Infine si puo' (deve?) aggiungere qualche dettaglio in piu' sull'ultima
affermazione. Il fatto cioe' di aver provato che uno degli h1 e' multiplo di uno
degli h'2 implica la stessa relazione fra l'elemento degli h1 e uno degli
elementi (inizialmente scelti) in uno degli hi con i>2. Questo deriva dal fatto
che se un elemento degli h1 e' multiplo di uno degli h'2 o lo e' di uno degli h2
(e quindi il discorso e chiuso) oppure lo e' di uno "riportato" dai sottoinsiemi
di indice maggiore. Ma se uno degli h1 e' multiplo di un elemento "riportato" lo
e' a maggior ragione dell'elemento "genitore".
(*) PIU GRANDE e NON PIU' PICCOLO perche sono stato "costretto" ad indicizzare
gli insiemi della partizione in un certo senso "contromano", questo mi continua
a creare problemi nell'esposizione. ma credo che l'altra scelta mi avrebbe dato
problemi maggiori.
6. Divisibile e divisore in una sequenza
Si scelgano n+1 interi fra i primi 2n. Ce n'è almeno uno divisibile per un'altro.
P. Erdös, 1937
Dimostrazione inviata da Giorgio Tumelero
Costruiamo il mobile En, contenente i numeri da 1 a 2n in questo modo:
nel cassetto C1 mettiamo il numero dispari 1 e tutti i suoi (eventuali)
raddoppiamenti;
nel cassetto C2 mettiamo il numero dispari 3 e tutti i suoi (eventuali)
raddoppiamenti;
...
nel cassetto Cr mettiamo il numero dispari 2r-1 e tutti i suoi (eventuali)
raddoppiamenti;
...
nel cassetto Cn mettiamo il numero dispari 2n-1.
Facciamo un esempio per n=7.
En = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14)
C1 = (1, 2, 4, 8)
C2 = (3, 6, 12)
C3 = (5, 10)
C4 = (7, 14)
C5 = (9)
C6 = (11)
C7 = (13)
Tornando al caso generale, qualunque sia n, il mobile En contiene n cassetti e,
per il principio dei cassetti, prendere n+1 oggetti da n cassetti significa che
da un qualche cassetto bisogna obbligatoriamente prendere due oggetti, cioè due
numeri sono presi da uno stesso cassetto. Ma in qualsiasi coppia di numeri
estratta da uno stesso cassetto il numero più grande è sempre multiplo
dell'altro, il loro rapporto è sempre 2 o una potenza di 2 più grande.
CVD
Come è nata questa dimostrazione?
L'impostazione del problema mi faceva pensare alla teoria di Ramsey sulle
configurazioni nascoste in certi insiemi di punti, oggetto di studio nella
teoria dei grafi.
Costruiamo dunque il grafo Gn=(V,R) dove V è l'insieme dei 2n vertici e R è la
relazione "uno dei due è multiplo dell'altro".
Partiamo da n=1 e vediamo cosa succede aumentando sempre di uno.
G1 è formato dai vertici 1 e 2 uniti da una linea, G1=(1R2) è un grafo
semplicemente connesso.
Passiamo ad n=2 aggiungendo i vertici 3 e 4. Il vertice 3 rimane isolato, mentre
4 si unisce a 2 mediante una linea, G2=(1R2,2R4) + (3) ha due componenti
connesse.
Passiamo ad n=3 aggiungendo i vertici 5 e 6. Il vertice 5 rimane isolato, mentre
6, che avrebbe dovuto essere unito a 2 e a 3, m'è venuto naturale collegarlo
solo a 3, per maggior chiarezza del disegno, modificando dunque R in questo
modo: R adesso è la relazione "uno dei due è il doppio dell'altro; dunque
G3=(1R2,2R4) + (3R6) + (5) ha tre componenti connesse.
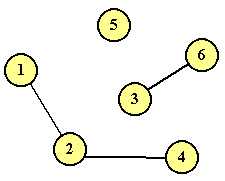
Ecco che balza all'occhio la dimostrazione: per quanto aumenti n, Gn ha sempre n componenti connesse e prendere n+1 vertici di Gn significa, per il principio dei cassetti, che due vertici devono essere per forza presi nella stessa componente connessa. Ma ogni componente connessa contiene una serie geometrica a, 2a, 2*2a, 2*2*2a, ... e di due qualsiasi termini di questa serie uno dei due è multiplo dell'altro...
Nota.
Nel luglio 2007 ho riunito tre pagine del sito dedicate al principio dei
cassetti in questa unica pagina.
---
Pace e bene a tutti.
GfBo
Data creazione: 2003
Ultimo aggiornamento: maggio 2020
xhtml 1.1
Sito Web realizzato da Gianfranco Bo