[HOME - BASE Cinque - Appunti
di Matematica ricreativa]
I regoli di Golomb
da un'idea di Solomon W. Golomb
1. Il righello col minimo numero di marche
Qual è il minimo numero di tacche (o marche) da fare su un
listello di legno per poter misurare, centimetro per centimetro, tutte le
distanze da 1 a 11 cm?
Ogni distanza deve essere misurata con una sola operazione.
(Variante a Dudeney, 1920)
2. Il righello massimo con 4 marche
Leggete con attenzione il testo del problema.
Come abbiamo visto nel problema precedente, non è necessario che un righello
abbia le marche ad ogni centimetro per poter misurare tutte le
possibili distanze multiple del centimetro.
Qual è il più lungo righello che si può costruire, tale che con 4 marche
possa misurare tutte le distanze multiple del centimetro, da 1 cm fino
alla lunghezza del righello stesso?
Ovviamente la lunghezza del righello deve essere un numero intero di centimetri.
Ogni distanza deve essere misurata con una sola operazione.
3. Il regolo di Golomb
Vuoi mettere esattamente 4 marche su un righello in modo da poter misurare ,
centimetro per centimetro, tutte le distanze da 1 cm in avanti.
Ogni distanza deve essere misurata con una sola operazione.
Qual è la massima distanza a cui puoi arrivare?
Ovvero: quanto è lungo il righello?
4. Sei punti su una circonferenza
Come si possono disporre 6 punti su una circonferenza in modo da poter
misurare tutti gli angoli multipli di 18° ovvero tutti gli archi multipli di
1/20 di circonferenza?
(Dudeney, 1921)
5. Organizzazione
Hai 13 persone, che devi fare incontrare 4 alla volta per 13 volte in modo
che ciascuno incontri tutti gli altri.
Come organizzi gli incontri?
6. I pesi della bilancia
Hai una bilancia a bracci uguali.
Qual è il minimo sistema di pesi necessario per pesare chilo per chilo tutti i
pesi da 1 a 40 kg?
7. L'ingegnoso mercante
Un commerciante si ritrova al mercato con la sua bilancia a bracci uguali ma
ha dimenticato a casa i pesi.
Nel suo furgone trova i seguenti oggetti:
- una barra di ferro lunga 80 cm e pesante 40 kg;
- un metro;
- un seghetto per metalli.
Come riuscirà, con 3 soli tagli, a ottenere dalla barra di ferro un sistema di
pesi che gli permetta di pesare chilo per chilo tutti i pesi da 1 a 40 kg?
8. I pesi della bilancia generalizzato
Hai una bilancia a bracci uguali.
Puoi comprare soltanto n pesi.
Quali pesi scegli, se vuoi pesare, chilo per chilo, tutti i pesi da 1 al più
alto peso possibile?
9. Le resistenze elettriche
La resistenza elettrica si misura in Ohm.
- Collegando due resistenze a, b, in serie, si ottiene una
resistenza pari alla somma delle due:
R = a + b
- Collegando due resistenze in parallelo si ottiene una
resistenza data dalla seguente relazione:
1/R = 1/a + 1/b
Qual è il minimo sistema di resistenze necessario per ottenere Ohm per Ohm
tutte le resistenze da 1 a 36 Ohm?
Nota storica.
Dudeney. Problem 518: The damaged measure. Strand Mag. (Sep 1920) ??NX. Wants a
minimal ruler for 33 inches total length. (=? MP 180)
Dudeney. Problem 530: The six cottagers. Strand Mag. (Jan 1921) ??NX. Wants 6
points on a circle to give all arc distances 1, 2, ..., 20. (=? MP 181)
P. A. MacMahon. The prime numbers of measurement on a scale. Proc. Camb. Philos.
Soc. 21 (1922-23) 651-654. He considers the infinite case, i.e. a(0) = 0, a(i+1)
= a(i) + least integer which is not yet measureable. This gives: 0, 1, 3, 7, 12,
20, 30, 44, ....
fonte: David Singmaster
Ultimo aggiornamento: gennaio 2006
Risposte & riflessioni
Un po' di teoria
(Note tratte e rielaborate da: Lorenzo
Francesco Castiglioni, Righelli di Golomb / Golomb's Rulers)
Un regolo (o righello) di Golomb è costituito da una serie
di numeri interi.
Questi numeri sono chiamati marche e corrispondono a posizioni su di
una scala lineare.
Ad esempio, nel regolo qui sotto, le marche sono: (0, 1, 4, 6)
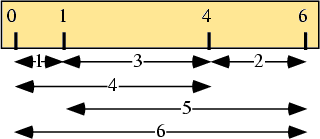
La prima marca viene messa per default a 0.
Le marche sono situate, rispetto alla marca 0, in posizioni multiple intere
di una distanza assegnata. Perciò le marche sono indicate con numeri
interi.
La differenza tra due marche qualsiasi è detta distanza tra le due
marche.
La differenza tra la marca piú grande e quella piú piccola del regolo é
detta lunghezza del regolo.
La distanza tra due marche, tra cui ne sono presenti altre n, è detta differenza
dell'n-esimo ordine.
Se la distanza tra due marche qualsiasi del regolo é unica (cioé, non
esistono altre coppie di marche appartenenti al regolo che generano la
stessa distanza), il regolo è detto regolo di Golomb.
L'obiettivo dei regoli di Golomb è quello di
ottenere il massimo numero di misure distinte con un dato
numero di marche.
Perciò le marche devono essere situate in modo efficiente, cioè
tale da evitare distanze ridondanti. Ciò significa che la distanza
di ciascuna marca da ogni altra deve essere unica.
Ad esempio le marche:
0--1--2--3
Non sono disposte in modo efficiente perché esistono 3 coppie separate
dalla distanza 1: (0,1), (1,2), (2,3) e 2 coppie separate dalla distanza 2:
(0,2), (1,3).
Non costituiscono un rigello di Golomb.
Un regolo di Golomb é perfetto se le distanze che
origina sono tutti i numeri tra 0 e la sua lunghezza.
Un regolo di Golomb é ottimo se ha la minima lunghezza fissato un
certo numero di marche. Dato un certo numero di marche, ci possono essere
diversi righelli di Golomb ottimi (in breve, OGR).
Un esempio di regolo di Golomb a 4 marche è: (0, 1, 3, 7)
0--1-----3-----------7
Può misurare 6 lunghezze distinte: 1, 2, 3, 4, 6, 7. Manca la 5.
Non è perfetto.
Un esempio di regolo di Golomb perfetto a 4 marche è: (0,
1, 4, 6)
0--1--------4-----6
Ecco un esempio di regolo di Golomb ottimo a 5 marche: (0,
1, 4, 9, 11)

Con esso sono possibili le seguenti misure: 1, 2, 3, 4, 5,
7, 8, 9, 10, 11. Manca la 6, quindi il regolo è ottimo ma non perfetto.
Esistono righelli di Golomb perfetti soltanto fino a 4
marche.
L'immagine speculare di un regolo di Golomb é a sua volta un regolo di
Golomb.
Un regolo di Golomb si "scrive" come elenco, racchiuso fra
parentesi tonde, di numeri interi separati da virgole.
|
Righelli di Golomb ottimi
|
numero
marche |
righelli ottimi |
| 2 |
(0, 1) |
| 3 |
(0, 1, 3) |
| 4 |
(0, 1, 4, 6) |
| 5 |
(0, 1, 4, 9, 11)
(0, 2, 7, 8, 11) |
| 6 |
(0, 1, 4, 10, 12, 17)
(0, 1, 4, 10, 15, 17)
(0, 1, 8, 12, 14, 17)
(0, 1, 8, 11, 13, 17) |
| 7 |
(0, 1, 4, 10, 18, 23, 25)
(0, 2, 3, 10, 16, 21, 25)
(0, 1, 11, 16, 19, 23, 25)
(0, 1, 7, 11, 20, 23, 25)
(0, 2, 7, 13, 21, 22, 25) |
| 8 |
(0, 1, 4, 9, 15, 22, 32, 34) |
|
1. Il righello col minimo numero di marche
Certamente dovrai mettere una marca a 0 e una a 11.
Se poi aggiungi le marche 1, 2, 3, 7 potrai effettuare tutte le misure
richieste.
In tutto sono 6 marche.
Vediamo come.
0..1..2..3...........7...........11
|--|--|--|-----------|-----------|
Con questo sistema puoi misurare certamente 1, 2, 3 cm.
Ma puoi anche misurare, per differenza, tutte le altre distanze, infatti:
4 = 7-3
5 = 7-2
6 = 7-1
7 = 7-0
8 = 11-3
9 = 11-2
10 = 11-1
11 = 11-0
Questo NON è un regolo di Golomb.
Il problema non è risolvibile con meno di 6 marche.
Utilizzando 6 marche, il problema ha in tutto 30 soluzioni. Eccole.
---
Marche: ( 0 , 1 , 2 , 3 , 7 , 11 )
Misure ottenibili:
0 1 1 1 2 2 3 4 4 5 6 7 8 9 10 11
---
Marche: ( 0 , 1 , 2 , 5 , 8 , 11 )
Misure ottenibili:
0 1 1 2 3 3 3 4 5 6 6 7 8 9 10 11
---
Marche: ( 0 , 1 , 2 , 5 , 9 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 4 5 6 7 8 9 9 10 11
---
Marche: ( 0 , 1 , 2 , 6 , 8 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 6 7 8 9 10 11
---
Marche: ( 0 , 1 , 2 , 6 , 9 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 7 8 9 9 10 11
---
Marche: ( 0 , 1 , 2 , 7 , 8 , 11 )
Misure ottenibili:
0 1 1 1 2 3 4 5 6 6 7 7 8 9 10 11
---
Marche: ( 0 , 1 , 2 , 7 , 10 , 11 )
Misure ottenibili:
0 1 1 1 2 3 4 5 6 7 8 9 9 10 10 11
---
Marche: ( 0 , 1 , 3 , 4 , 9 , 11 )
Misure ottenibili:
0 1 1 2 2 3 3 4 5 6 7 8 8 9 10 11
---
Marche: ( 0 , 1 , 3 , 5 , 10 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 7 8 9 10 10 11
---
Marche: ( 0 , 1 , 3 , 6 , 10 , 11 )
Misure ottenibili:
0 1 1 2 3 3 4 5 5 6 7 8 9 10 10 11
---
Marche: ( 0 , 1 , 4 , 5 , 9 , 11 )
Misure ottenibili:
0 1 1 2 3 4 4 4 5 5 6 7 8 9 10 11
---
Marche: ( 0 , 1 , 4 , 6 , 9 , 11 )
Misure ottenibili:
0 1 2 2 3 3 4 5 5 5 6 7 8 9 10 11
---
Marche: ( 0 , 1 , 4 , 7 , 9 , 11 )
Misure ottenibili:
0 1 2 2 3 3 4 4 5 6 7 7 8 9 10 11
---
Marche: ( 0 , 1 , 4 , 9 , 10 , 11 )
Misure ottenibili:
0 1 1 1 2 3 4 5 6 7 8 9 9 10 10 11
---
Marche: ( 0 , 1 , 5 , 8 , 9 , 11 )
Misure ottenibili:
0 1 1 2 3 3 4 4 5 6 7 8 8 9 10 11
---
Marche: ( 0 , 1 , 5 , 8 , 10 , 11 )
Misure ottenibili:
0 1 1 2 3 3 4 5 5 6 7 8 9 10 10 11
---
Marche: ( 0 , 1 , 6 , 7 , 9 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 6 7 8 9 10 11
---
Marche: ( 0 , 1 , 6 , 8 , 10 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 7 8 9 10 10 11
---
Marche: ( 0 , 2 , 3 , 6 , 10 , 11 )
Misure ottenibili:
0 1 1 2 3 3 4 4 5 6 7 8 8 9 10 11
---
Marche: ( 0 , 2 , 4 , 5 , 10 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 6 7 8 9 10 11
---
Marche: ( 0 , 2 , 4 , 7 , 10 , 11 )
Misure ottenibili:
0 1 2 2 3 3 4 4 5 6 7 7 8 9 10 11
---
Marche: ( 0 , 2 , 5 , 7 , 10 , 11 )
Misure ottenibili:
0 1 2 2 3 3 4 5 5 5 6 7 8 9 10 11
---
Marche: ( 0 , 2 , 5 , 9 , 10 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 7 8 9 9 10 11
---
Marche: ( 0 , 2 , 6 , 7 , 10 , 11 )
Misure ottenibili:
0 1 1 2 3 4 4 4 5 5 6 7 8 9 10 11
---
Marche: ( 0 , 2 , 6 , 9 , 10 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 4 5 6 7 8 9 9 10 11
---
Marche: ( 0 , 2 , 7 , 8 , 10 , 11 )
Misure ottenibili:
0 1 1 2 2 3 3 4 5 6 7 8 8 9 10 11
---
Marche: ( 0 , 3 , 4 , 9 , 10 , 11 )
Misure ottenibili:
0 1 1 1 2 3 4 5 6 6 7 7 8 9 10 11
---
Marche: ( 0 , 3 , 5 , 9 , 10 , 11 )
Misure ottenibili:
0 1 1 2 2 3 4 5 5 6 6 7 8 9 10 11
---
Marche: ( 0 , 3 , 6 , 9 , 10 , 11 )
Misure ottenibili:
0 1 1 2 3 3 3 4 5 6 6 7 8 9 10 11
---
Marche: ( 0 , 4 , 8 , 9 , 10 , 11 )
Misure ottenibili:
0 1 1 1 2 2 3 4 4 5 6 7 8 9 10 11
---
2. Il righello massimo con 4 marche
Il righello più lungo è 13 cm (o 13 unità).
Se il righello è lungo esattamente 13 cm, la marca iniziale (0) e quella finale
(13) non vanno segnate.
Le 4 marche richieste saranno tutte interne al righello.
Questo problema ha 6 soluzioni, tutte ridondanti, quindi non si tratta di un
regolo di Golomb.
---
Marche: ( 0 , 1 , 2 , 6 , 10 , 13 )
Misure ottenibili:
0 1 1 2 3 4 4 5 6 7 8 9 10 11 12 13
---
Marche: ( 0 , 1 , 4 , 5 , 11 , 13 )
Misure ottenibili:
0 1 1 2 3 4 4 5 6 7 8 9 10 11 12 13
---
Marche: ( 0 , 1 , 6 , 9 , 11 , 13 )
Misure ottenibili:
0 1 2 2 3 4 5 5 6 7 8 9 10 11 12 13
---
Marche: ( 0 , 2 , 4 , 7 , 12 , 13 )
Misure ottenibili:
0 1 2 2 3 4 5 5 6 7 8 9 10 11 12 13
---
Marche: ( 0 , 2 , 8 , 9 , 12 , 13 )
Misure ottenibili:
0 1 1 2 3 4 4 5 6 7 8 9 10 11 12 13
---
Marche: ( 0 , 3 , 7 , 11 , 12 , 13 )
Misure ottenibili:
0 1 1 2 3 4 4 5 6 7 8 9 10 11 12 13
---
Qui sotto riporto un banalissimo programma in BASIC che trova le soluzioni.
(con il copia e incolla si è persa l'indentazione)
!'posizioni delle marche e tutte le differenze possibili
DIM p(20)
DIM diff(20)
!'n è il numero totale di tacche del righello completo, in questo caso da 0 a
13
!'per trovare il valore massimo, per un certo numero di marche, va variato in un
certo range per tentativi
LET n=14
!'nm è il numero di marche stabilito, compresi i due estremi del righello
LET nm=6
LET p(1)=0
LET p(nm)=n-1
FOR a=1 TO n-1
LET p(2)=a
FOR b=a TO n-1
LET p(3)=b
FOR c=b TO n-1
LET p(4)=c
FOR d=c TO n-1
LET p(5)=d
!'--------
!'Calcola tutte le differenze
LET cont=1
LET diff(cont)=0
FOR h=1 TO nm-1
FOR k=h+1 TO nm
LET cont=cont+1
LET diff(cont)=p(k)-p(h)
NEXT k
NEXT h
!'Ordina differenze
FOR h=1 TO cont
FOR k=h TO cont
IF diff(k)<diff(h) THEN
LET tp=diff(h)
LET diff(h)=diff(k)
LET diff(k)=tp
END IF
NEXT k
NEXT h
!'Verifica che ci siano tutti i valori interi
FOR u=0 TO n-1
LET ok=0
FOR v=1 TO cont
IF diff(v)=u THEN LET ok=1
NEXT v
IF ok=0 THEN EXIT for
NEXT u
!'Se ci sono risultati, li stampa
IF ok=1 THEN
PRINT "Marche: (";
FOR j=1 TO nm
PRINT p(j);",";
NEXT j
PRINT ")"
PRINT "Misure ottenibili: "
FOR j=1 TO cont
PRINT diff(j);
NEXT j
print
PRINT "---"
END IF
!'--------
NEXT d
NEXT c
NEXT b
NEXT a
print"Finito!"
END
3. Il regolo di Golomb
La risposta, già data, è (0, 1, 4, 6).

4. Sei punti su una circonferenza
5. Organizzazione
Un particolare ringraziamento a GioFulmine per la seguente
soluzione. Grazie!
Ti mando anche la soluzione di un problema che c'è nel tuo sito,
visto che si riferisce a cose di cui sono ora interessato. Si trova nel capitolo
dedicato alla Combinatoria, "I righelli di Golomb". Bisogna far
incontrare 13 persone a gruppi di 4, ci ho messo poco, avendo anche avuto la
fortuna di non sbagliare mai, quindi senza dover tornare indietro a far
variazioni.
Numerando le persone con i numeri da 1 a 13, i gruppi sono:
1 2 4 7
1 3 8 9
1 5 10 13
1 6 11 12
2 3 12 13
2 5 6 8
2 9 10 11
3 4 6 10
3 5 7 11
4 5 9 12
4 8 11 13
6 7 9 13
7 8 10 12
6. I pesi della bilancia
Con (1,3,9,27) si arriva fino a 40 kg
7. L'ingegnoso mercante
Beh, se avete risolto il problema precedente avete in mano anche la souzione
di questo problema.
Siccome 1+3+9+29=40 e la barra, supposta omogenea etc., è lunga 80 cm, il
mercante la taglia a: 2, 6, 18 cm.
I pesi, però, saranno un po' più leggeri del dovuto perchè il seghetto,
tagliando, asporta una piccola quantità di ferro sotto forma di limatura.
Questo fatto, ovviamente, torna a vantaggio del mercante!
8. I pesi della bilancia generalizzato
La sequenza (1, 2, 4, 8, 16, ...) tenta molto perché ogni numero intero si può
ottenere come somma di potenze di 2.
Ma nella bilancia a bracci uguali i pesi possono essere posti su entrambi i
piatti e quindi si possono fare misure, oltre che per somma, anche per
differenza.
La sequenza migliore, in effetti, è (1, 3, 9, 27, 81, ...) perché ogni numero
intero può essere ottenuto come somma algebrica di potenze di 3.
num.
pesi |
sistema più efficiente di pesi |
peso massimo |
| 1 |
1 |
1 |
| 2 |
1,3 |
4 |
| 3 |
(1,3,9) |
13 |
| 4 |
(1,3,9,27) |
40 |
| 5 |
(1,3,9,27,81) |
121 |
Il peso massimo misurabile con n pesi è (3^n-1)/2
9. Le resistenze elettriche
Ehm... la soluzione di questo esercizio è lasciata al lettore...
Ringrazio Pasquale per la seguente risposta.
A riguardo dei "Regoli di Golomb" di cui alla home-page e
del quesito sulle resistenze necessarie per formare tutti i valori da 1 a 36
ohm, mi pare sufficiente combinare in tutti i modi possibili 6 resistenze da 1,
2, 4, 8, 16 e 32 ohm, utilizzando solo accoppiamenti in serie, per ottenere
tutti i valori da 1 a 63 ohm (forse per 36 potrebbero esserne sufficienti 5,
sfruttando anche qualche parallelo, ma non mi è riuscito di trovare i valori
giusti che lo permettano).
Più genericamente, attribuendo ad "n" resistenze i valori delle
potenze del 2 da 2^0 a 2^(n-1) , è possibile ottenere tutti i valori da 1 a 2^n
-1: stabilita una certa resistenza da ottenere, basta effettuare la
trasformazione del valore da decimale a binario, scegliere quelle in
corrispondenza degli 1 e metterle in serie. Per valori da 1 a 2^n-1 ritengo che
il sistema sia minimizzato e senza ridondanze.
Sito Web realizzato da Gianfranco Bo

