[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Un problema vecchio come le colline si risveglia come un vulcano
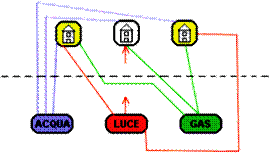
Tre case, tre servizi
Ci sono tre case e tre fonti: una d'acqua, una di elettricità e una di
gas. E' possibile collegare ciascuna casa con ciascuna fonte per mezzo di
linee che stiano sullo stesso piano e non si incrocino?
Nota storica.
Questo problema fu pubblicato da Henry Earnst Dudeney col titolo
"Water, gas, and electricity" su Strand Magazine nell'agosto del
1913.
"There are some half-dozen puzzles, as old as the hills, that are
perpetually cropping up, and there is hardly a month in the year that does
not bring inquiries as to their solution. Occasionally one of these, that one
had thought was an extinct volcano, bursts into eruption in a surprising
manner. I have received an extraordinary number of letters respecting the
ancient puzzle that I have called "Water, Gas and Electricity". It is much
older than electric lighting, or even gas, but the new dress brings it up to
date. The puzzle is to lay on water, gas, and electricity, from W, G and E,
to each of the three houses, A, B and C, without any pipe crossing
another."
Un po' di teoria.
Testo e figure tratte da Giuseppe Biorci, Fondamenti di elettrotecnica
e circuiti, UTET, 1975. E' il libro in cui ho letto per la prima volta
del collegamento tra questo gioco e Kuratowskj.
"Una rete si dice "piana" o "planare" se è possibile distendere il suo
grafo su un piano, in modo che non vi restino incroci di lati. La fig. 6-8
mostra un grafo piano, che può essere disegnato anche con incroci. La fig.
6-9 mostra invece un grafo che non è piano, perché comunque lo si disegni,
resta sempre in esso un incrocio di lati.
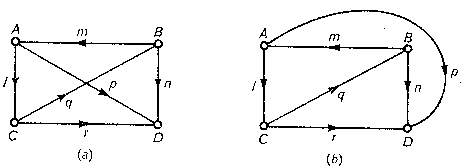
fig. 6-8
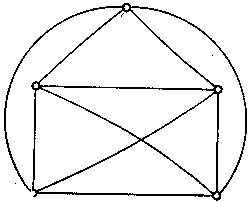
fig. 6-9
Molte reti della pratica sono
piane, ma non tutte. Ad esempio, i cosiddetti circuiti stampati a doppio
rame, cioè quelli che hanno piste di connessione su entrambe le facce della
cartolina, servono appunto a realizzare connessioni che, se attuate su una
sola faccia, imporrebbero incroci di collegamenti. È stato dimostrato che,
se una rete non è piana, il suo grafo deve contenere almeno una delle
seguenti figure:
a) un pentagono completo, cioè con tutte le diagonali, (fig. 6-9), oppure
b) un poligono di Kuratowski del terzo ordine, intendendo con questo il grafo
illustrato in fig. 6-10."
(La dimostrazione è per l'appunto di Kasimierz Kuratowskj,
1930)
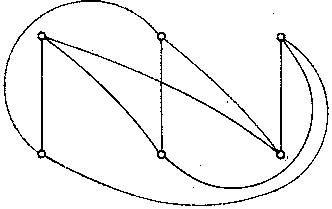
fig. 6-10
Lo stesso Dudeney dice che il problema è vecchio come le
colline e che non passa mese che qualcuno non prova a risolverlo.
Jim Loyd ci ha provato e sembra esserci riuscito! Diventerà famoso?
La soluzione di Jim Loyd
Prima di affrontare un problema difficile conviene allenarsi con alcuni più facili.
Otto strade senza incroci
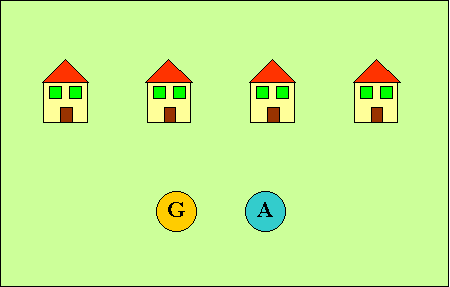
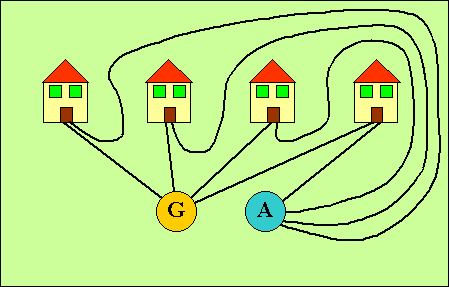
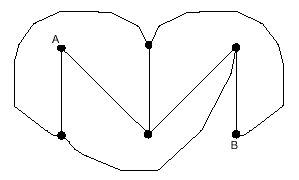
Quattro fattorie si devono rifornire periodicamente di grano al granaio G
e di acqua al pozzo A.
Per motivi che non esamineremo qui, ciascun proprietario vuole costruire due
strade separate che partano dalla sua fattoria e che conducano
rispettivamente al granaio e al pozzo. Inoltre nessuna strada deve
incrociarsi con un'altra.
Come si può risolvere questo problema?
Se le fattorie, anziché quattro, fossero 5, 6, 7, ... sarebbe ancora
possibile risolvere il problema?
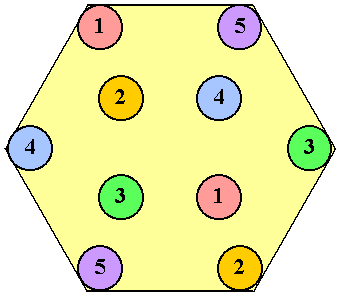
Intelligenza elettrica
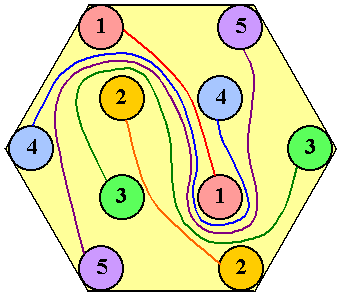
Un elettricista deve completare il seguente schema elettrico collegando
fra di loro i cerchi che hanno lo stesso colore (e anche lo stesso numero):
il rosso con il rosso (n.1), il giallo con il giallo (n.2), e così via. I
cavi di collegamento non devono mai incrociarsi né uscire dallo schema
esagonale.
Come farà?
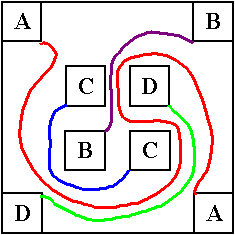
Camillino e il suo cellulare
Camillino è impegnatissimo col suo telefono cellulare. Sta facendo un
videogioco che presenta il seguente schema.

Bisogna collegare fra di loro 8 quadratini per mezzo 4 linee
nel modo seguente:
- il quadratino A deve essere collegato con l'altro quadratino A, il B con il
B, il C con il C e il D con il D;
- le linee che li congiungono non possono né incrociarsi, né toccare i bordi
dello schermo.
E alla fine... ritorniamo all'inizio
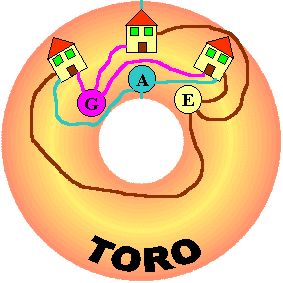
Tre case, tre servizi, un toro
Chiediamoci:
- perché non è possibile risolvere questo problema sul piano?
- esiste una superficie sulla quale è possibile risolvere questo problema?
Immaginiamo di vivere su un pianeta a forma di toro (praticamente un
classico salvagente).

In questo pianeta ci sono tre case e tre fonti: una d'acqua, una di elettricità e una di gas. E' possibile collegare ciascuna casa con ciascuna fonte per mezzo di linee che non si incrocino e che giacciano sulla superficie del pianeta?
Tre case, tre servizi
La soluzione di Jim Loyd è uno scherzo! I colori delle linee ci aiutano a
capire che C è collegato 2 volte con Z e B è collegato 2 volte con con X.

Otto strade senza incroci
Intelligenza elettrica
Camillino e il suo cellulare
Tre case, tre servizi, un toro
Grazie a Enrico Ricci per la seguente soluzione.
La soluzione potrebbe essere effettuando l'ultimo collegamento piegando il foglio o forandolo e facendo l'ultimo collegamento sul retro del foglio stesso.
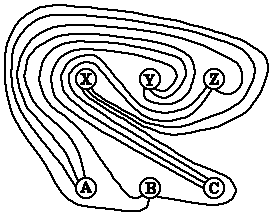
Perché K33 non è risolvibile nel piano?
Cominciamo con la spiegazione intuitiva inviata da John Conway a MathForum.
On Sun, 18 Jan 2004, John Berglund wrote:
> It is impossible unless you bend the rules
(like allowing one of the lines to pass underneath a house.)
>
> Here is the simplest way of explaining this that I know:
Call the houses A,B,C. Call the utilities X,Y,Z.
[I now simplify John's explanation.]
Then the lines A--Z, Z--B, B--X, X--C, C--Y, Y--A form a
closed circuit, which can be distorted so as to look like a
hexagon:-
| A | -- | Z | ||||
| / | \ | |||||
| Y | B | |||||
| \ | / | |||||
| C | -- | X |
But now we must supplement this by the three
diameters A--X, B--Y, C--Z
each of which must either lie entirely inside the hexagon or entirely
outside. But we can have at most one lying inside (for if two, they
must cross), and similarly at most one lying outside - a contradition.
John Conway
Seguono poi due risposte molto interessanti che si trovano anche nelle Ricreazioni di Marzo 2001:
Giofulmine
Il buon vecchio Eulero ha scoperto una formula magica per i poliedri (semplici) che dice:
V - S + F = 2
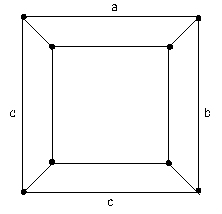
ovvero il numero V dei vertici meno il numero S degli spigoli più il numero F delle facce dà sempre 2 come risultato. Ora, qualsiasi poliedro (semplice) può essere proiettato nel piano semplicemente appoggiando una sua faccia nel foglio e schiacciando tutte le altre all'interno, come nell' esempio sotto del cubo (fig. 1).
Qualcuno potrebbe obiettare che il cubo ha 6 facce e nel disegno ce ne sono solo 5; infatti nella proiezione si considera esista una faccia infinita in più, il bianco che circonda la figura, una faccia delimitata dai lati a, b, c, d, quella appoggiata per prima. Questo per qualsiasi poliedro.
Viceversa, qualsiasi grafo planare è la proiezione di un qualche poliedro.
Come si vede in figura 1, per il cubo abbiamo V = 8, S = 12, F = 6. Ancora, ciascuna faccia è circondata da 4 spigoli e siccome ci sono 6 facce, abbiamo 24 spigoli (questo perché ogni spigolo è comune a due facce quindi viene contato due volte) ovvero:
2S = 4F, cioè 2*12 = 4*6
Passiamo adesso a disegnare il grafo K 3,3 (fig. 2):
Per maggior chiarezza manca ancora lo spigolo che collega i vertici A e B. Come si vede ci sono 3 facce più la faccia infinita più la faccia che si otterrebbe collegando A e B, cioè F = 5, risultato ottenibile anche dalla formula di Eulero:
6 - 9 + F = 2 ovvero F = 2 - 6 + 9 = 5
Paolo Hagler
Il fatto di poter disegnare un grafo (dei vertici uniti con determinate linee) su un piano è chiamato il problema di planarità del grafo.
Per prima cosa si osservi che se esistono due linee parallele (ossia che uniscono lo stesso paio di punti) una delle due si può eliminare ed il problema è lo stesso.
Osserviamo ora un grafo planare (disegnabile sul piano senza che nessun paio di lati si intersechi)
Esso ha V vertici, E lati, e S poligoni (di cui uno esterno).
Siccome ogni poligono ha almeno 3 lati ed un lato divide sempre e solo due poligoni sappiamo che 2E³3S
A questo punto dobbiamo utilizzare il teorema d'Eulero, che afferma che un grafo pianare topologico connesso con V vertici, E lati e S poligoni verifica P=E-V+2 (caso particolare del teorema dei poliedri)
Quindi abbiamo 2E³3(E-V+2)=3E-3V+6
E di conseguenza 3V³E+6
Questa propietà è verificata da ogni grafo planare
K3,3 verifica questa proprietà, tuttavia esiste una forma più ristretta di questa proprietà per i grafi bipartiti come K3,3
Un grafo bipartito è tale che i vertici si possono dividere in due gruppi, e non esiste alcun lato tra due vertici dello stesso gruppo
In questo caso ogni poligono ha almeno 4 lati (non esistono poligoni con un numero dispari di lati)
Quindi abbiamo 2E³4(E-V+2)=4E-4V+8
E di conseguenza 2V³E+4
Questa propietà è verificata da ogni grafo planare bipartito
Ora K3,3 è bipartito e possiede 6 vertici e 9 lati, pertanto non verifica 2V³E+4 che è una proprietà dei grafi planari bipartiti
Dim. Teorema d'Eulero
(per induzione su E)
Partiamo dal grafo più semplice, V=1, E=0
Abbiamo S=1 e quindi la proprietà è verificata
Prendiamo ora un grafo che verifichi la proprietà (ipotesi d'induzione) ed aggiungiamoci un lato (E aumenta di 1)
a) se aggiungendo un lato aggiungo anche un vertice, S rimane invariato, e la formula vale ancora
b) altrimenti S aumenta di 1 e la formula resta valida
giugno 2004
Sito Web realizzato da Gianfranco Bo