[BASE Cinque - Appunti di Matematica ricreativa]

Punti nel piano
a distanze reciproche razionali (o intere)

Traduzione e commento del teorema di Erdos-Anning

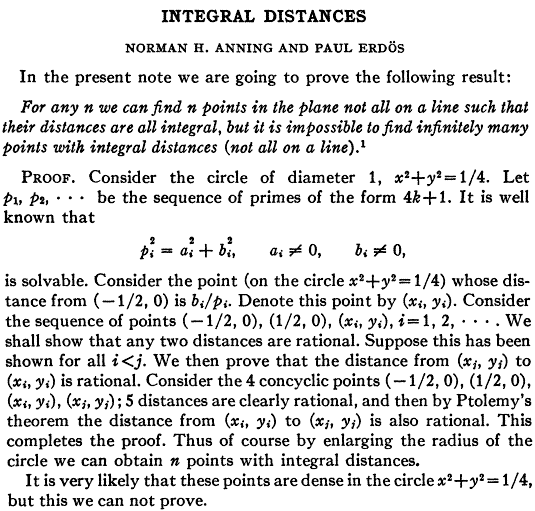
INTEGRAL DISTANCES

NORMAN H. ANNING AND PAUL ERDÖS

In the present note we are going to prove the following result:

For any n we can find n points in the plane not all on a line such that their distances are all integral, but it is impossible to find infinitely many points with integral distances (not all on a line).

PROOF. Consider the circle of diameter 1, x²+y²=1/4.

Let p₁, p₂, ... be the sequence of primes of the form 4k+1.

It is well known that

p_i² = a_i²+b_i², a≠0, b≠0,

is solvable.

Consider the point (on the circle x²+y²=1/4) whose distance from (-1/2, 0) is b_i/p_i.

Denote this point by (x_i, y_i).

Consider the sequence of points (-1/2, 0), (1/2, 0), (x_i, y_i), i=1, 2, ... .

We shall show that any two distances are rational.

Suppose this has been shown for all i<j.

We then prove that the distance from (x_j, y_j)to (x_i, y_i)is rational.

Consider the 4 concyclic points (-1/2, 0), (1/2, 0), (x_j, y_j), (x_i, y_i); 5 distances are clearly rational, and then by Ptolemy's theorem the distance from (x_i, y_i), (x_j, y_j) is also rational.

This completes the proof.

Thus of course by enlarging the radius of the circle we can obtain n points with integral distances.

It is very likely that these points are dense in the circle x²+y²=1/4, but this we can not prove.

Data creazione: marzo 2013

Ultimo aggiornamento: marzo 2013

xhtml 1.1

Sito Web realizzato da Gianfranco Bo