[HOME - BASE Cinque - Appunti di Matematica ricreativa]
ovvero l'involuta del cerchio
Ringrazio Paolo P. per aver
inviato questo problema al Forum.
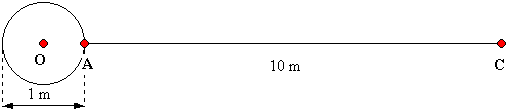
Il cane, la corda e la colonna cilindrica
A una colonna cilindrica di 1 m di
diametro, che ha centro in O, è fissato un anello A.
All'anello è attaccata una corda di lunghezza 10 m, tesa in
direzione OA.
Alla corda è attaccato un cane C. Il cane inizia a correre,
mantenendo sempre tesa la corda.
Che distanza ha percorso il cane quando la corda si è avvolta di
un giro completo intorno alla colonna?

Se il problema vi sembra difficile, provate prima con quello seguente.
Il cane, la corda e la colonna quadrata
A uno spigolo di una colonna a base quadrata
di 1 m di lato, che ha centro in O, è fissato un anello A.
All'anello è attaccata una corda di lunghezza 10 m, tesa in
direzione OA.
Alla corda è attaccato un cane C. Il cane inizia a correre, (nel
verso indicato dalla freccia arancione) mantenendo sempre tesa la
corda.
Che distanza ha percorso il cane quando la corda si è avvolta di
un giro completo intorno alla colonna?

Il cane, la corda e la colonna cilindrica
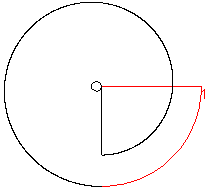 |
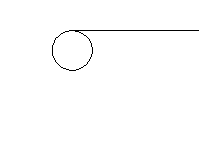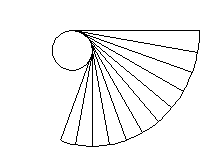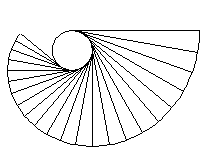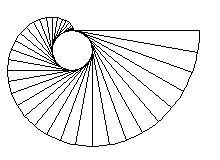 Involuta della circonferenza |
La traiettoria percorsa dal cane è un tratto di
involuta di una circonferenza di raggio 0,5 cm.
La lunghezza s (o ascissa curvilinea)
dell'involuta è data dalla seguente funzione:
s = a*t2/2
dove a è il raggio della circonferenza e t è il numero
di giri espresso in radianti.
Devo dapprima trovare di quanti giri occorre
svolgere la corda per arrivare a liberarne 10 m di lunghezza.
angolo = 10 /(2*pi*0,5) giri = 3,183*2*pi
radianti
La traiettoria percorsa è lunga:
s1 = 0,5*(3,183*2*pi)^2/2 m = 100 m
La traiettoria per un giro di meno è lunga:
s2 = 0,5*(2,183*2*pi)^2/2 m = 47,038 mLa
differenza fra le due lunghezze è:
s1-s2 = 52,962 m
A questi devo aggiungere 1/4 di circonferenza di raggio 10 m
s3 = 2*pi*10/4 = 15,71 m
Il percorso totale è:
s1-s2+s3 = 68,672 m
MaMo
La curva descritta dal cane è un tratto dell'involuta di una
circonferenza di raggio 0,5 m.
Se non ho sbagliato i conti, la sua lunghezza è:
pi*(25 - pi) = 68,67 m.
Pasquale
Anche a me sembra che il percorso sia costituito da un quarto di
circonferenza di raggio 10 (finché la corda non è tangente alla
colonna) e da una curva che rassomiglia ad un segmento di spirale.
Non so se è la stessa cosa che ha detto il grande Mamo, nè come
si eseguono questi calcoli, ma intuitivamente procedo così:
Primo tratto = 2*pi*r/4 = 5*pi
Secondo tratto = media fra la circonferenza di raggio massimo (10)
e la circonferenza di raggio minimo (10-pi)
Totale:
5*pi + (20*pi - pi^2) = pi(25 - pi) = 68,67
Il cane, la corda e la colonna quadrata
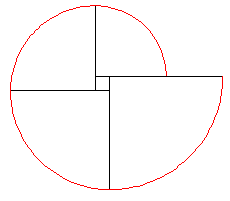 Caso 1 |
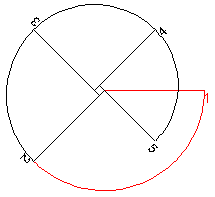 Caso 2 |
Se la colonna è a sezione quadrata, si hanno
diversi casi, a seconda della direzione iniziale della corda.
Nel caso 1 (il disegno non è in scala), la distanza percorsa dal
cane è pari a 4 quarti di circonferenze di raggi 10, 9, 8, 7 m
rispettivamente.
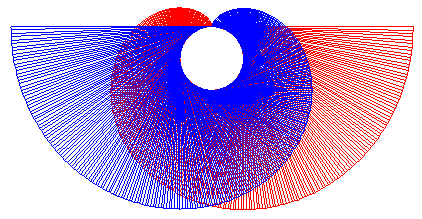
L'involuta può rappresentare una corda che si
avvolge ad un cerchio
ma anche una corda che si svolge.
L'involuta della circonferenza e la spirale di Archimede.
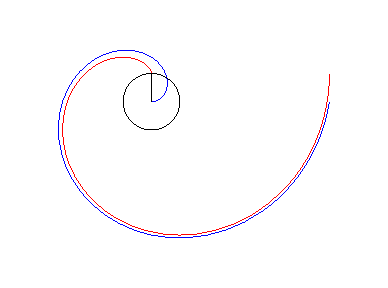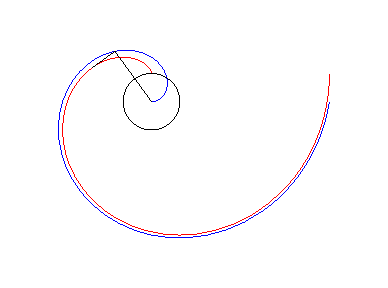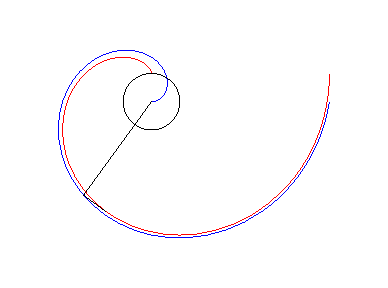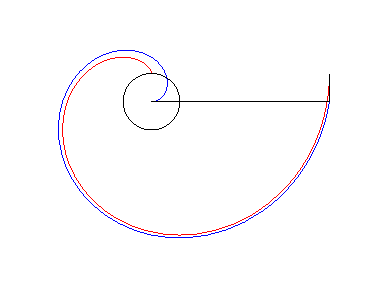
Non sono proprio identiche ma sono parenti
strette.
L'involuta (rossa) è asintotica alla spirale (blu).
Equazione parametrica dell'involuta del
cerchio.
Centro O, raggio a, contatto (a,0)
x = a(cos(t) + t*sin(t)
y = a(sin(t) + t*cos(t)
Equazione polare.
a*t = sqr(r2-a2)
- a*arccos(a/r)
Lunghezza (o ascissa curvilinea).
s = a*t2/2
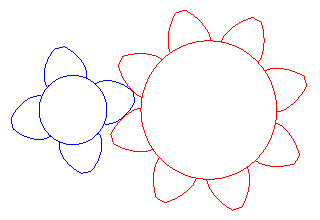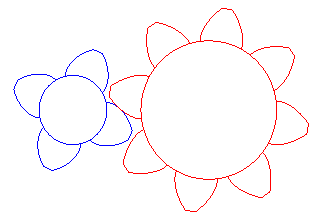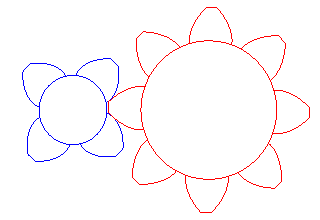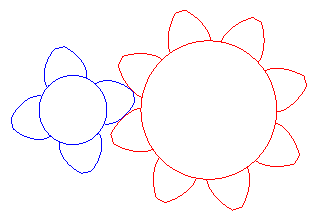
I denti di molti ingranaggi hanno la forma
dell'involuta della circonferenza.
Tale caratteristica è particolarmente esagerata in questo
disegno.
Grazie a questa forma, i denti rotolano l'uno sull'altro senza
strisciare.
Così l'attrito è più basso e non c'è usura.
luglio 2004
Sito Web realizzato da Gianfranco Bo