[HOME - BASE Cinque - Appunti
di Matematica ricreativa]
Il problema della galleria d'arte
Quanti guardiani servono e dove bisogna piazzarli per
sorvegliare una galleria d'arte?
Immaginate di essere i proprietari di una Galleria d'Arte. Fra
pochi giorni la vostra Galleria ospiterà un'esposizione di quadri del famoso
pittore Pablo Dalì.
Poiché i quadri esposti sono preziosissimi, ogni punto della
galleria deve essere sorvegliato costantemente a vista da fidati guardiani.
Dovete però ridurre al minimo le spese di sorveglianza.
Le domande quindi sono:
Occorre inoltre tener conto delle seguenti informazioni:
 |
Ogni guardiano, simboleggiato con un bollino rosso, ha un campo
visivo di 180°, cioè può vedere davanti a sé, alla propria destra, e
alla propria sinistra, ma non dietro di sé. A ciascun guardiano viene
assegnata una posizione fissa dalla quale può vedere una certa zona
della Galleria.
|
 |
Se la pianta del locale da sorvegliare è un poligono convesso, è
sufficiente un solo guardiano posto in un qualunque punto del perimetro.
|
 |
Se invece la pianta è un poligono concavo, cioè ha delle
"rientranze", allora un solo guardiano potrebbe non essere sufficiente.
Nella figura, per esempio, il guardiano può vedere tutto il locale tranne
la zona colorata di grigio.
|
---
Il primo piano
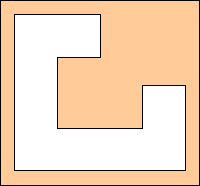
Il primo piano della vostra Galleria d'Arte ha la seguente pianta.
Impiegherete tre guardiani per sorvegliarlo o ve ne basteranno soltanto due?
---
Il secondo piano
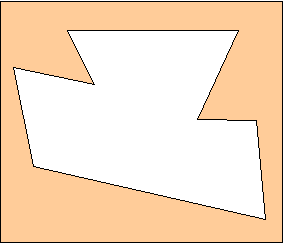
Questa è la pianta del secondo piano. Potete farla sorvegliare interamente
da un solo guardiano, ma qual è la posizione giusta?
---
Il terzo piano
Ed ecco la pianta del terzo piano. Qui il compito è un po' più difficile:
dovete utilizzare il numero minimo di guardiani e fare anche in modo che si
vedano a vicenda

---
L'attico
Siamo giunti finalmente all'attico. La sua pianta è simmetrica e abbastanza
semplice, ma vi basterà un solo guardiano per farla sorvegliare interamente?

---
Esiste una strategia generale per affrontare questo problema?
Riformuliamo il problema così, passando dai guardiani alle telecamere:
- Quante telecamere situate sui vertici della pianta di
un locale, avente la forma di un poligono semplice di n lati, sono necessarie e
sufficienti per sorvegliare tutti i punti del locale
stesso?
- Quante telecamere situate
sui vertici della pianta di un locale, avente la forma di un poligono
semplice di n lati, e contenente h "fori" sono necessarie e sufficienti per sorvegliare tutti i punti del locale stesso?
Le telecamere hanno un campo visivo di 360°
(si può supporre che ruotino velocemente)
I "fori" sono ostacoli alla visuale. Si possono immaginare come colonne, con la pianta a forma di poligono semplice,
che vanno dal pavimento al soffitto.
Nota storica.
Il problema fu posto per la prima volta da Victor Klee nel 1973 in
una discussione con Vasek Chvatal.
"Quante guardie situate sui vertici della pianta di un locale, avente la
forma di un poligono semplice di n lati, sono necessarie e
sufficienti
per sorvegliare tutti i punti del locale stesso?"
Vasek Chvatal, nel 1975, ha dimostrato che sono sufficienti floor(n/3)
guardie.
Nel 1978 Steve Fisk ne ha dato una dimostrazione più semplice basata
sulla triangolazione del poligono e la colorazione a tre colori dei vertici dei
triangoli.
Tale triangolazione senza aggiunta di vertici a quelli del poligono
è garantita dal teorema delle due orecchie "Two Ears Theorem" di Gary Meister.

Vasek (Vaclav) Chvatal 1946 |

Victor Klee (1925-2007) |
 Steve Fisk
(1946-2010)
|
Bjorling-Sachs e Souvaine (1991,
1995) e Hoffman et al. (1991) hanno dimostrato che per sorvegliare un locale di
n lati e contenente h fori sono sufficienti floor((n+h)/3) guardie.
Chvátal, Vasek, A combinatorial theorem in plane geometry, JCT (B), 18 (1975)
39-41.
Fisk, Steve, A short proof of Chvátal's watchman theorem, JCT (B) 24 (1977) 374.
La funzione matematica floor(a) è l'arrotondamento del numero reale a
all'intero superiore.
Per esempio, floor(7/3) = 3.
Risposte & riflessioni
Il primo piano
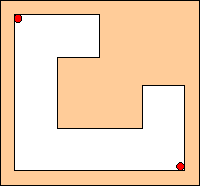
Il primo piano della vostra Galleria d'Arte ha la seguente pianta.
Impiegherete tre guardiani per sorvegliarlo o ve ne basteranno soltanto due?
Il secondo piano
Questa è la pianta del secondo piano. Potete farla sorvegliare interamente
da un solo guardiano, ma qual è la posizione giusta?
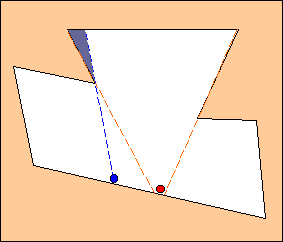
La posizione esatta è segnalata dal bollino rosso. In qualunque
altra posizione, ad esempio quella occupata dal bollino blu, una parte del
locale non è visibile.
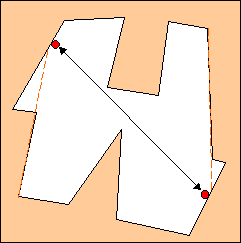
Il terzo piano
Ed ecco la pianta del terzo piano. Qui il compito è un po' più difficile:
dovete utilizzare il numero minimo di guardiani e fare anche in modo che si
vedano a vicenda
L'attico
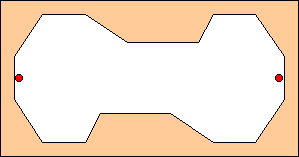
Siamo giunti finalmente all'attico. La sua pianta è simmetrica e abbastanza
semplice, ma vi basterà un solo guardiano per farla sorvegliare interamente?
---
Pace e bene a tutti.
GfBo
Data creazione: aprile 2005
Ultimo aggiornamento: novembre 2025
html5
Sito Web realizzato da Gianfranco Bo













