 |
 |
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Un particolare ringraziamento a Paquale per aver postato il seguente problema al Forum.
Il nastro adesivo
Una bobina vuota ha il diametro di 2 cm e su questa arrotoliamo
un nastro adesivo di 1/2 mm di spessore: al termine del primo
giro il nastro si accavalla su quello sottostante e quindi si
avvolge a spirale, compiendo 30 giri.
Si può determinare quanto è lungo il nastro?
Forse potremmo
approssimare la lunghezza del nastro a quella di tante
circonferenze sempre più grandi avvolte attorno alla bobina.
Forse potremmo pensare che il nastro formi una spirale di
Archimede.
Ma se osserviamo meglio la realtà, scopriamo che è più
complessa dei suoi modelli.
Potete rendervene conto esaminando le due scansioni qui sotto di
un vecchio nastro biadesivo.
Ho scelto un nastro piuttosto spesso per mettere meglio in
evidenza lo "scalino" che si forma nei punti di "accavallamento"
del nastro. Questo fenomeno è stato esaminato da Cesarone e da
Infinito.
Una piccola sfida
Se volete mettere alla prova le vostre strategie risolutive, vi
propongo una piccola sfida.
 |
 |
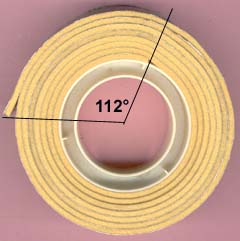
Ho preso un rocchetto di nastro biadesivo espanso e l'ho svolto completamente.
Ho misurato il diametro della bobina con
un calibro di precisione 1/20 mm.
Diametro della bobina: 36,3 mm
Ho inoltre valutato, osservando la figura
e utilizzando un goniometro scolastico:
Numero di giri: 7 + 112°
Per quel che riguarda lo spessore del
nastro, ho provato a misurarlo con il calibro, ma siccome
il nastro stesso è morbido, risulta difficile ottenere
una misura precisa.
Forse è meglio misurare lo spessore di vari strati col
righello e dividere per il numero degli strati.
Potete farlo voi stessi osservando la scansione qui sotto.
Il righello è millimetrato.

Ho realizzato le scansioni dopo aver riavvolto il nastro senza "tirarlo" ma lasciandolo aderire liberamente alla bobina, con una leggerissima pressione delle dita.
Prima di riavvolgere il nastro, ho misurato la sua lunghezza con un metro da falegname.
Quanto è lungo il nastro?
Una prima approssimazione: la spirale di
Archimede.
Potremmo ipotizzare che il nastro avvolto attorno alla
bobina approssimi una spirale di Archimede.
L'approssimazione è plausibile poiché lo spessore del nastro è
costante.
Se approssimiamo il nastro ad una spirale di Archimede,
la risposta è: il nastro è lungo circa 334,58 cm.

Simulazione del problema realizzata
con il Decimal BASIC di Shiraishi Kazuo
La spirale di Archimede ha la seguente equazione
polare: r = a*t
Il passo della spirale, cioè la distanza costante
fra due spire successive è: d = 2*pi*a
Conoscendo il passo, si può determinare a: a = d/(2*pi)
La lunghezza della spirale è: L =![]()
dove "theta" è il numero di giri in radianti e a è il
passo.

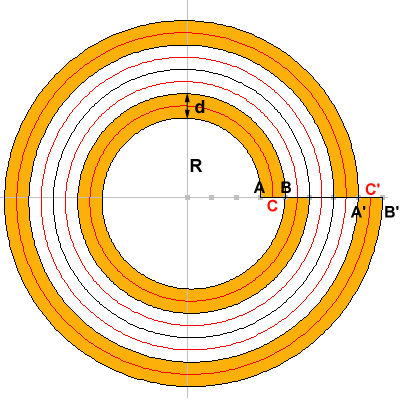
La spirale del nostro problema interseca l'asse x
nei punti multipli dello spessore del nastro.
r = t/(40*pi)
| Se lo
spessore del nastro è importante e vogliamo tenerne
conto. La figura a destra mostra un nastro:
Piegando il nastro,
Qual è allora la lunghezza esatta del nastro quando sarà svolto?
|
 |
Nel caso del problema:
LET d=0.5 !'spessore
nastro
LET a=d/(2*PI) !'fattore della spirale
LET rb=20/2 !'raggio bobina
LET t0=(rb/d)*2*PI !'numero giri fino a inizio nastro
LET t1= t0+(30)*2*PI !'numero giri fino a fine nastro
LET L1=(1/2)*a*(t1*SQR(1+t1^2)+LOG(t1+SQR(1+t1^2))) !'lunghezza
totale spirale
LET L0=(1/2)*a*(t0*SQR(1+t0^2)+LOG(t0+SQR(1+t0^2))) !'lunghezza
spirale fino a inizio nastro
LET LS=(L1-L0) !'lunghezza nastro
PRINT LS
Se poniamo rb=20/2, otteniamo la lunghezza della spirale
interna.
LS=329,87 cm
Se poniamo rb=20/2+d/2,
otteniamo la lunghezza della spirale media, che è il valore
migliore.
LS=334,58 cm
Se poniamo rb=20/2+d, otteniamo la lunghezza della spirale
esterna.
LS=339,30 cm
Ho ricevuto varie critiche alla mia simulazione e
anche alla mia soluzione basata sulla spirale di Archimede.
Perciò riporto anche altre soluzioni alcune delle quali
decisamente più precise, in ordine di arrivo al Forum.
| La soluzione di
Pasquale-Ronfo Prima versione. Seconda versione. |
| La soluzione di
Cesarone Posto che il nastro sia
perfettamente flessibile, quindi che lo si possa piegare
a 90° (trascurando compressione e trazione ai bordi
nella curva a 90°) io non ci vedo nessuna spirale... Preciso che va considerata la circonferenza con raggio medio, perchè solo nel "mezzo" abbiamo l'unica linea non soggetta a deformazione, che rappresenta quindi la reale lunghezza del nastro di partenza non deformato. Allora se il primo giro è lungo: Sottolineo che il fulcro del problema sta nel
fatto che il nastro non può essere considerato privo di
spessore, quindi va trovata una linea appartenente al
nastro che rimane indeformata e quindi ci garantisce una
misura accurata della lunghezza, come da nastro non
avvolto. |
| La soluzione di
Infinito Non vi ho seguito molto bene (soprattutto
per quanto riguarda la spirale), ma vi propongo il mio
tipo di approssimazione, che mi pare più adeguata (cioè
che si discosta "pochissimo" dalla realtà e
che rimane comunque abbastanza semplice da trattare) di
quella del salto a gradino. Somma per k che va da 0 a 29 di (2·pi_greco·(r+0,5·s+k·s)+ L0-((r+0,5·s+k·s)·arcsen(L0/((r+0,5·s+k·s)+s))) con r=1 , s=0,05 , L0=radice_quadrata(s²+2·s·(r+0,5·s+k·s)) ) il cui valore in
risposta è 330,109 (valore per eccesso) il valore
completo è stato 330,10884254117) che indica 330,11 cm.
Ricordo che la lunghezza «reale» (ammesso che abbia un senso) dovrebbe essere leggermente minore, anche se «a occhio» stimo che le cifre della risposta che ho dato siano tutte corrette, la ripeto: 3,3011 metri. |
Una piccola sfida
Il nastro svolto è lungo 114 cm.
Per la valutazione dei risultati è molto importante la seguente osservazione di Infinito.
"Se ben ricordo il nastro biadesivo ha un supporto «cartaceo» molto rigido e tale da deformarsi molto meno (a pari forze) del nastro vero e proprio (insieme della parte spugnosa e delle colle). La struttura complessiva è tale che tende a far comprimere la faccia del nastro più vicina alla bobina."
| Approssimazione | INTERNA | MEDIA | ESTERNA |
| alle circonferenze Pasquale |
105.0 | 108.8 | 112.5 |
| circonferenze + tratto rettilineo MaMo |
--- | 110.2 | 113.4 |
| circonferenze + tratti di raccordo Infinito |
--- | 110.8 | 114.3 |
| circonferenze + tratto rettilineo +
raccordo Cesarone |
--- | 111.0 | 114.7 |
| Spirale di Archimede Gianfranco |
110.6 | 114.4 | 118.0 |
Se accettiamo l'ipotesi di Infinito, cioè che il
valore più corretto è quello esterno, allora il risultato che
più si avvicina al valore reale (per ora) è quello di...
Infinito, con un errore dello 0,003%
seguito a pari merito da...
MaMo, con un errore dello 0,005%
CESARONE, con un errore dello 0,006%
Infinito ha inviato una
dettagliato intervento al Forum, nel quale spiega la formula che
ha utilizzato.
La formula è:
(Somma per k che va da 0 a
6 di
(2·pi_greco·(r+s+k·s)+ L0-((r+s+k·s)·arcsen(L0/((r+s+k·s)+s))))+(112/360·(2·pi_greco·(r+8s))))
con r=3.63/2 , s=1,12/7 , L0=radice_quadrata(s²+2·s·(r+s+k·s))
Ho tradotto la sua formula nel seguente programma BASIC per verificare il risultato.
LET ls=0
LET r=3.63/2
LET s=1.12/7
LET ng=7
FOR k=0 TO ng-1 !'Somma per k che va da 0 a 6
LET v=r+s+k*s
LET L0=SQR(s^2+2*s*v)
LET ls=ls+(2*PI*v+L0-(v*ASIN(L0/(v+s))))
NEXT k
LET ls=ls+(112/360*(2*PI*(r+8*s))) !'Aggiunta dell'ultimo pezzo
PRINT ls
Cesarone mi ha inviato un disegno, assieme alla spiegazione del suo metodo.
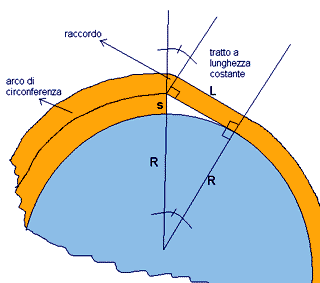
Dipende molto in ogni modo da come hai effettuato
l'avvolgimento... se sei riuscito a non applicare
veramente alcun tiro e sei riuscito a far semplicemente aderire
il nastro ad ogni giro. Dalla foto sembra quasi di sì.
Allora se il nastro aderisce perfettamente a quello che gli sta
sotto, considerando che il primo accavallamento avviene con
segmento rettilineo tangente alla bobina, si ha che ogni giro è
composto da:
1) un arco di circonferenza pari al 93,5122% della circonferenza
di raggio r = R + s/2 + (n-1)*s
2) un tratto rettilineo di lunghezza fissa L = 0,7838 cm
3) un raccordo di angolo ampiezza = 23,256° e raggio r = n*s
- s/2
dove:
n: è il numero di giro
s = 0,162 cm è lo spessore
R = 1,815 cm è il raggio della bobina
L'arco mancante si ricava così:
arccos[R/(R+s)] = 23,356°
Per cosiderazioni geometriche ovvie, l'ampiezza del raccordo
corrisponde proprio alla parte mancante di circonferenza, infatti:
(360 - 23,356)/360 = 0,93512(2)
Inoltre si ha: 23,356° / 360° = 0,064878
Pertanto con 7 giri otteniamo:
Sum(n=1:7) [2*pi*[R + s/2 + s*(n-1)]*0,935122 + L + 2*pi*(n*s
-s/2)*0,064878]
Dopodichè va aggiunto l'ottavo giro parziale di 112°.
In pratica con l'arco mancante di circonferenza pari a 23,356°
come mi risulta dalle misurazioni fatte, si ottiene una lunghezza
finale del nastro di:
111 cm
facendo variare l'arco tra 10° e 30° ottengo i valori:
110,71 cm ---- 111,37 cm
Anche in questo caso ho verificato la soluzione di Cesarone con il seguente programma BASIC.
LET ls=0
LET L=0.7838
LET s=0.162
LET R=1.815
FOR n=1 TO 7
LET ls= ls+(2*PI*(R + s*(n))*0.935122 + L + 2*PI*(n*s)*0.064878)
NEXT N
LET aggiunta=(2*PI*(R + s + s*(7))*0.935122 + L + 2*PI*(8*s)*0.064878)*112/360
ls=ls+aggiunta
PRINT ls
luglio 2004
Sito Web realizzato da Gianfranco Bo