[BASE Cinque - Appunti di Matematica ricreativa]
Il principe dei quadrilateri
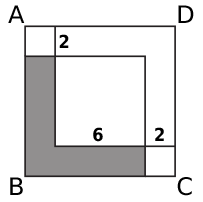
Area della L
Il quadrilatero ABCD è un quadrato. Dentro questo quadrato sono disegnati altri tre quadrati i cui lati misurano, in centimetri, come indicato nella figura.
Qual è l'area del poligono colorato di grigio?

Quanti quadrati (1)?
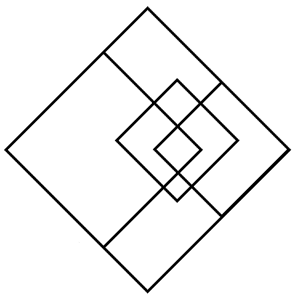
Quanti quadrati riuscite a distinguere nella seguente figura?
Con una sola linea continua
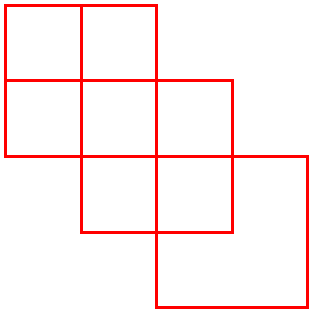
Riuscireste a disegnare la figura qui sotto tracciando una unica linea continua, senza mai staccare la penna dal foglio, passando una sola volta su ciascun segmento e senza incroci?
Quanti quadrati (2)?
Nella seguente griglia 5x5 si possono distinguere vari quadrati di
dimensioni che vanno da 1x1 a 5x5.
Quanti di questi quadrati contengono il cerchio nero che si trova al centro
della griglia?

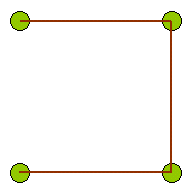
La rete stradale ottima
Quattro paesi sono situati in una grande pianura, ai vertici di un quadrato di lato 20 km. L'obiettivo è quello di costruire la rete stradale più corta possibile che metta in comunicazione ciascun paese con gli altri tre.
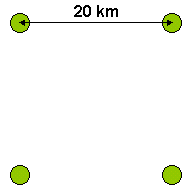
La seguente figura mostra una soluzione non ottimale del problema. In questo caso la rete stradale è lunga 60 km.
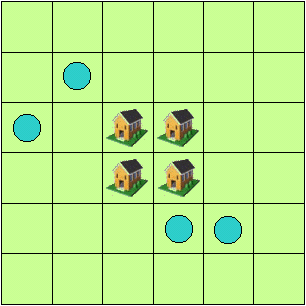
La divisione del podere
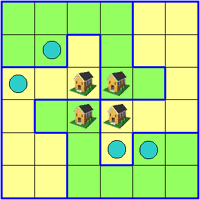
La piantina che vedete qui sotto rappresenta un podere formato da un grande
appezzamento di terreno agricolo nel quale si trovano 4 case coloniche e 4
pozzi. Il podere deve essere diviso in 4 parti uguali, sia per estensione sia
per forma, in modo che in ciascuna parte si trovi una casa e un pozzo.
Chi è capace di fare la divisione?
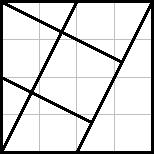
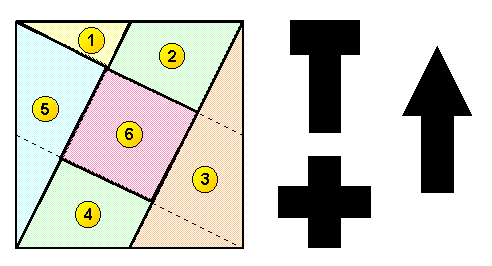
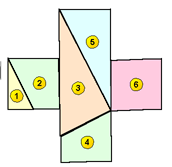
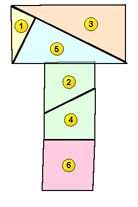
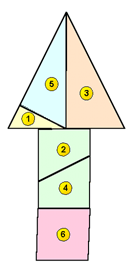
Dissezione del quadrato
Disegnate un quadrato su un cartoncino e sezionatelo in 6 parti come illustrato nella figura qui sotto. Le linee oblique congiungono ciascun vertice con il punto medio del lato opposto. Ritagliate le parti e ricomponetele in modo da formare una "T", una croce greca e una freccia. Per ogni figura dovete utilizzare tutti i sei pezzi del quadrato originario.
(questo esercizio è una variante di un classico di Samuel Loyd)
Area della L
28 cm2
Quanti quadrati (1)?
Nella figura si possono distinguere 7 quadrati.
Quanti quadrati (2)?

In totale: 1+4+9+4+1=19 quadrati contengono il cerchio nero.
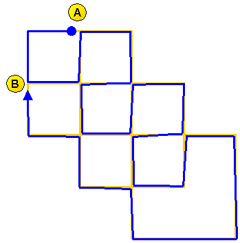
Con una sola linea continua
E' possibile tracciare la figura con una unica linea continua soltanto se si parte dal punto A oppure dal punto B. Qui sotto vedete una possibile soluzione. Le linee sono leggermente staccate nei punti di contatto per rendere più evidente il percorso seguito.
La rete stradale ottima
Una rete migliore di quella già vista è costituita dalle diagonali del quadrato. Il teorema di Pitagora ci permette di calcolare che è lunga circa 56,568 km. Inoltre, per andare da un paese a un qualunque altro, la distanza da percorrere è sempre la stessa, pari alla diagonale del quadrato. Tuttavia esiste una rete ancora più corta: è quella illustrata nella figura qui sotto.
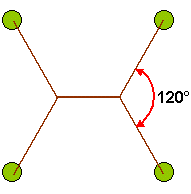
Sempre con l'aiuto di Pitagora possiamo calcolare che la rete è lunga circa 54,641 km, con un risparmio di circa 2 km rispetto al caso precedente.
La divisione del podere
Ecco una possibile soluzione
Dissezione del quadrato
Una piccola nota: per formare la freccia occorre ribaltare il triangolo grande, indicato con il numero 3.
Data creazione: ottobre 2012
Ultimo aggiornamento: ottobre 2012
xhtml 1.1
Sito Web realizzato da Gianfranco Bo