[HOME - BASE Cinque - Appunti di Matematica ricreativa]
La geometria dei Samurai giapponesi durante il periodo EDO (1603-1867)
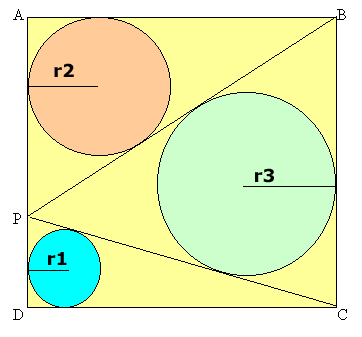
Sangaku 1
Il lato del quadrato ABCD vale 1.
Scelto un punto P sul lato AD, si divide il quadrato in tre triangoli con le
linee BP e CP.
Calcola le misure dei raggi dei tre cerchi inscritti nei triangoli.
Esiste un punto P per cui le misure dei tre raggi sono proporzionali ai numeri 1, 2, 3?

Sangaku 2
Le tre circonferenze sono tangenti alla retta orizzontale e ciascuna di esse
è tangente alle altre due.
Che relazione matematica c'é fra le misure dei loro tre raggi?

Sangaku 3
Un poligono convesso, che non sia un triangolo, inscritto in un cerchio può
essere triangolato in diversi modi. Ciascun triangolo ha un cerchio inscritto.
Dimostrare che in qualunque modo si triangoli un poligono inscritto in un
cerchio, la somma dei raggi dei triangoli inscritti è costante e indipendente
dalla triangolazione scelta.
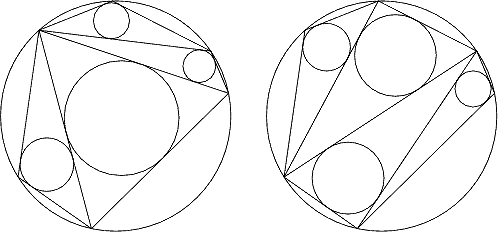
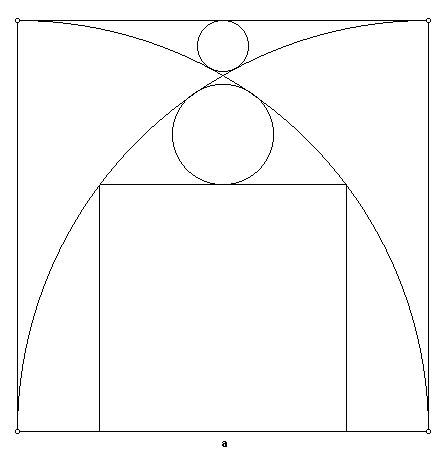
Sangaku 4
Calcola la misura del lato del quadrato interno e dei raggi dei cerchi in
funzione del lato del quadrato grande.
Ultimo aggiornamento: luglio 2005
Per risolvere alcuni problemi sangaku possono essere utili i seguenti due teoremi "occidentali".
Teorema di Carnot
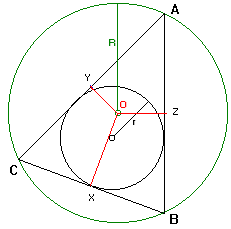
Teorema di Tolomeo
Il teorema di Tolomeo afferma che:
Se il quadrilatero ABCD è inscritto in una circonferenza, allora la somma dei
prodotti dei lati opposti è ugale al prodotto delle diagonali.
AB × DC + BD × AC = AD × BC
---
Sangaku 1
Grazie e complimenti a Antonio Palladino, che ha inviato la seguente soluzione.

Consideriamo in primo luogo il triangolo PDC: detta a la lunghezza del segmento
PD (a < 1), l'area A del triangolo PDC è:
![]()
Ma in un triangolo qualsiasi l'area è anche uguale al prodotto
del raggio del cerchio inscritto per la misura del semiperimetro; pertanto (dopo
aver calcolato con Pitagora la lunghezza dell'ipotenusa PC = ![]() ) si ha:
) si ha:
![]()
da cui:
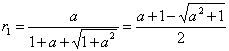
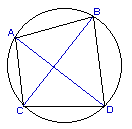
Analogamente, per il triangolo APB si ha:
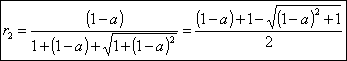
Infine, applicando lo stesso ragionamento al triangolo PBC, la cui area è pari a quella del quadrato, diminuita di quella dei due triangoli, si ha:
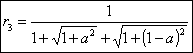
Imponendo r2 = 2·r1 si ottiene un'equazione irrazionale, che dà luogo ad un'equazione di 3° grado in a,
![]()
con soluzione accettabile (ricavata numericamente)
a = 0,282499930743…,
a cui corrispondono i raggi:
r1 = 0,121681…
r2 = 0,243363…
Il raggio r3 con il valore di a così trovato è pari a
r3 = 0,305819…, che non è il triplo di r1.
Pertanto (a mio avviso) non esiste un punto P tale per cui le misure dei raggi
siano proporzionali a 1, 2 e 3.
---
Sangaku 2
Grazie e complimenti a Antonio Palladino, che ha inviato la seguente soluzione.
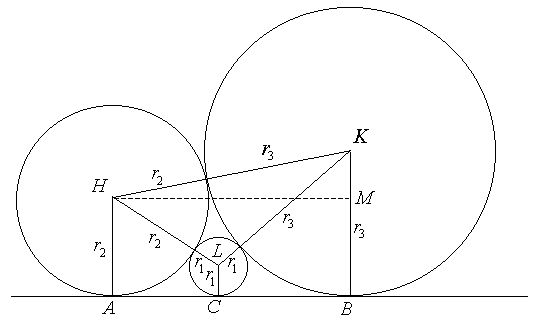
Si consideri il trapezio rettangolo ABKH: il segmento AB, che ne è altezza, misura quanto l'altra altezza HM, che può essere determinata con il teorema di Pitagora dall'ipotenusa HK e dal cateto KM:
![]()
Analoghe considerazioni si possono fare per gli altri due trapezi ACLH e BCLK, e risulterà in modo equivalente:
![]()
![]()
A questo punto, essendo AB = AC + CB, risulterà:
![]() ,
,
da cui, raccogliendo e risolvendo rispetto a ![]() , si ha:
, si ha:
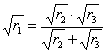
e infine, la relazione finale:
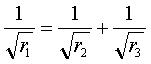
---
Sangaku 3
Grazie e complimenti a Antonio Palladino, che ha inviato la seguente soluzione.
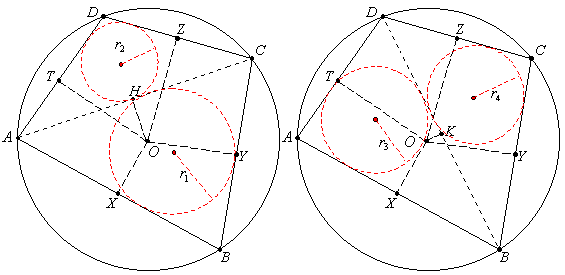
Consideriamo per semplicità un poligono di 4 lati inscritto
nella circonferenza di raggio R, il quadrilatero ABCD. Tracciando la diagonale
AC, esso si divide nei due triangoli ABC e ACD, pure inscritti nella
circonferenza.
Osserviamo che il il centro O della circonferenza maggiore è il circocentro del
triangolo ABC. Congiungiamo O con i lati AB, BC e AC, ottenendo i segmenti OX,
OY e OH. Sia r1 il raggio della circonferenza inscritta in ABC.
Applicando il teorema di Carnot al triangolo ABC si ha:
![]()
Si ripeta l'operazione per il triangolo superiore ACD: anche qui ovviamente, O è
circocentro per il triangolo; a differenza di prima O è esterno al triangolo.
Sia r2 il raggio della circonferenza inscritta in ACD. Siano OH, OZ e OT i
segmenti che congiungono O con i punti medi dei lati AC, CD e DA.
Applicando il teorema di Carnot al triangolo ACD si ha:
![]()
Nella formula davanti alla distanza OH appare il segno meno;
questo poiché nel teorema di Carnot la distanza del circocentro dal singolo lato
va considerata algebricamente, e in particolare positiva quando il circocentro
del triangolo si trova internamente rispetto al lato e negativa quando il
circocentro si trova esternamente rispetto al lato.
Addizionando membro a membro le due espressioni si ottiene:
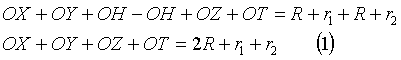
Ripetendo il ragionamento per la figura di destra si otterrà analogamente:
![]()
Confrontando la (1) con la (2) risulta
![]()
Il risultato precedente si può facilmente estendere a poligoni ciclici con più
di quattro lati.
---
Sangaku 4
Grazie e complimenti a Antonio Palladino, che ha inviato la seguente soluzione.
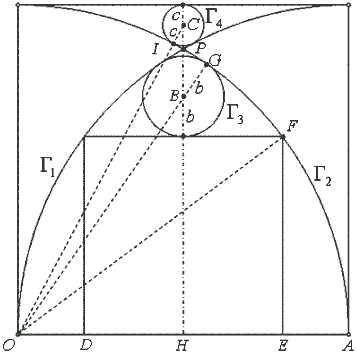
Per semplicità di calcolo suppongo che il lato del quadrato
maggiore sia unitario:
OA = a = 1.
Sia P il punto d'intersezione dei due archi Gamma1 e Gamma2; sia B il centro
della circonferenza Gamma3 tangente internamente Gamma1 e Gamma2 ed esternamente
il quadrato interno; sia C il centro della circonferenza Gamma4 tangente
esternamente Gamma1 e Gamma2 e internamente il quadrato esterno unitario. L'asse
verticale BPC è di simmetria per tutta la figura.
1) Vogliamo trovare il lato del quadrato interno; esso è disposto
simmetricamente rispetto all'asse CPD; indicato con l il suo lato, il triangolo
OEF è rettangolo; i suoi lati sono pari rispettivamente a:
![]()
Applicando il teorema di Pitagora si ha:
![]()
Si ottiene così l'equazione di secondo grado in l
![]()
che risolta, produce la soluzione accettabile
![]()
2) Vogliamo trovare ora il raggio b della circonferenza Gamma3. Si ha:
OG = OB + BG;
OG = 1; BG = b; OB è l'ipotenusa del triangolo rettangolo OBH; essa si può
ottenere attraverso Pitagora:
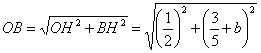
Sostituendo si ottiene l'equazione irrazionale
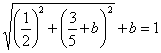
che risolta, dà la soluzione
![]()
3) Vogliamo infine trovare ora il raggio c della circonferenza Gamma4. Si ha:
OC = OI - IC;
OI = 1; IC = c; OC è l'ipotenusa del triangolo rettangolo OCH; essa si può ottenere attraverso il teorema di Pitagora:
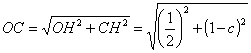
Sostituendo si ottiene l'equazione irrazionale:
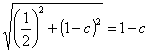
che risolta, dà la soluzione
![]()
Sito Web realizzato da Gianfranco Bo