[BASE Cinque - Appunti di Matematica ricreativa]

I giocattoli e la matematica: lo spirografo

In fondo a un cassetto ho ritrovato un vecchio spirografo.

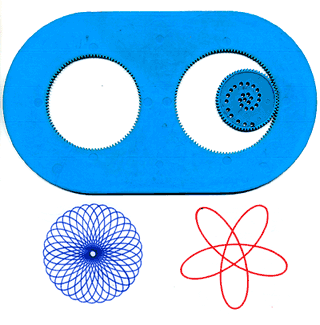
E' formato da un disco dentato che può rotolare all'interno di un anello anch'esso dentato. Il disco ha alcuni fori in cui si può inserire la punta di una penna.

Si appoggia lo spirografo su un foglio di carta, si inserisce la punta della penna in un foro e si fa rotolare il disco all'interno dell'anello, ottenendo così delle figure come quelle che vedete qui sotto.

1. Come si possono descrivere matematicamente tali curve?
2. Come si possono generare con un programma per computer?

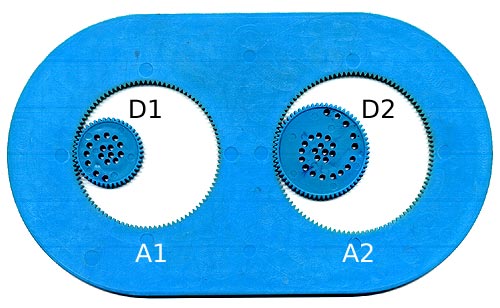
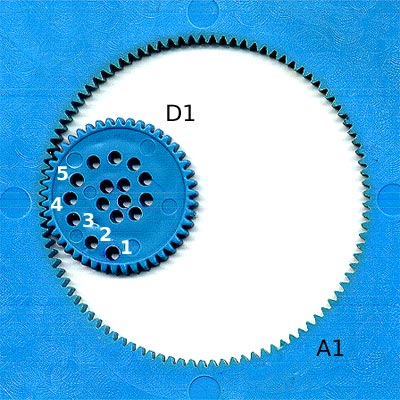
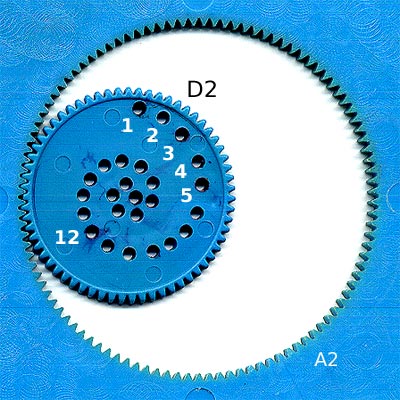
Ecco alcune figure generate con lo spirografo.

I tre codici sotto ogni figura indicano rispettivamente il disco, l'anello e il foro.

Come si possono descrivere matematicamente tali curve?

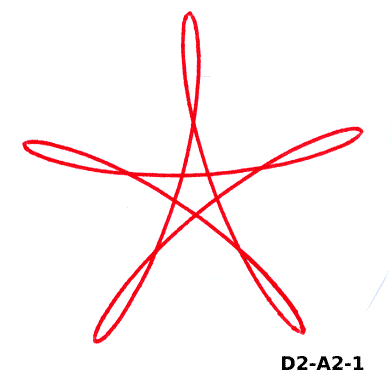
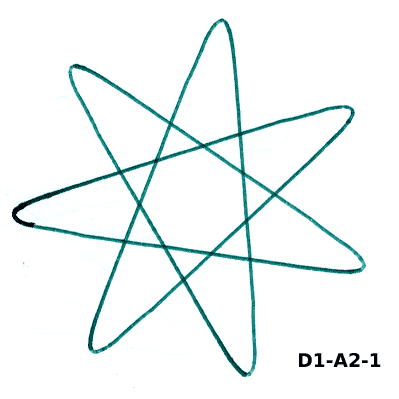
Le curve tracciate con lo spirografo si chiamano ipotrocoidi.

Per farla breve, le equazioni parametriche di una ipotrocoide sono:

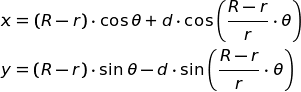
dove:

R = raggio dell'anello (cerchio grande fisso)

r = raggio del disco (cerchio piccolo rotante)

d = distanza del punto tracciante dal centro del disco

Per avere un'ipotrocoide, deve essere:

d<r

Un programma in DECIMAL BASIC che disegna le ipotrocoidi

!'Procedura che disegna un cerchio
SUB cerchio(cx, cy, r)
   FOR t=0*PI TO 2*PI STEP PI/180
      LET x=cx+r*COS(t)
      LET y=cy+r*SIN(t)
      PLOT LINES: x,y;
   NEXT t
   PLOT LINES: x,y
END SUB

!'Inizio programma
!'Disegna il quadro grafico
LET l=11
SET WINDOW -l,l,-l,l
SET LINE COLOR 8
PLOT LINES: -l,0;l,0
PLOT LINES: 0,-l;0,l

!'Fissa i parametri
LET r1=10
LET r2=4.285714
LET d=r2-r2/4
LET Dr=r1-r2
 
SET LINE COLOR 8
SET POINT STYLE 4

!'Disegna il cerchio grande e il suo centro
CALL cerchio(0,0,r1)
SET POINT COLOR 10
PLOT POINTS: 0,0

!'Disegna il cerchio piccolo e il suo centro
CALL cerchio(Dr,0,r2)
SET POINT COLOR 10
PLOT POINTS: Dr,0

!'Traccia il punto iniziale
SET POINT COLOR 4
LET cx=Dr+d
LET cy=0
PLOT POINTS: cx,cy
 
!'Disegna l'ipo/epi-trocoide
SET LINE COLOR 9
FOR t=0*PI TO 7*PI STEP PI/360
   LET x=Dr*COS(t)+d*COS((DR/r2)*t)
   LET y=Dr*SIN(t)-d*SIN((DR/r2)*t)
   PLOT LINES: x,y;
NEXT t
END

Il programma, con i parametri impostati, genera la seguente figura.

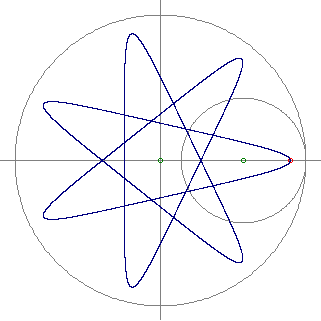
Per generare altre figure, bisogna inserire parametri diversi nelle seguenti linee del programma.

!'Fissa i parametri
LET r1=10
LET r2=4.285714
LET d=r2-r2/4
LET Dr=r1-r2

dove:

r1 = raggio dell'anello (fisso)

r2 = raggio del disco (rotante)

d = distanza del punto tracciante dal centro del disco

Pace e bene a tutti!

Gianfranco Bo

Data creazione: ottobre 2014

Ultimo aggiornamento: ottobre 2014

xhtml 1.1

Sito Web realizzato da Gianfranco Bo