
[BASE Cinque - Appunti di Matematica ricreativa]
Come
si può ottenere una stella a cinque punte di carta con un solo taglio
diritto?
E soprattutto, perché il metodo funziona?
E' facile ottenere una stella a 2, 4, 8, 16, ... punte.
Basta piegare un foglio di carta opportunamente a metà, poi di nuovo a metà, e così via e alla fine tagliare via un pezzo che contenga l'incrocio di tutte le pieghe.

3 pieghe = 4 assi di simmetria = stella a quattro punte.

4 pieghe = 8 assi di simmetria = stella a 8 punte.
In generale:
n pieghe = stella a 2(n-1) punte.
Le proporzioni del foglio di carta non hanno alcuna importanza: il gioco riesce sempre.
Per ritagliare una stella a 5 punte in un colpo solo non vale più il metodo visto prima perché 5 non è una potenza di 2.
Esiste tuttavia una procedura abbastanza semplice, ma richiede che il foglio sia un rettangolo di determinate proporzioni.
Una delle proposte più comuni è quella di preparare un foglio rettangolare di 8,5 x 10 unità.
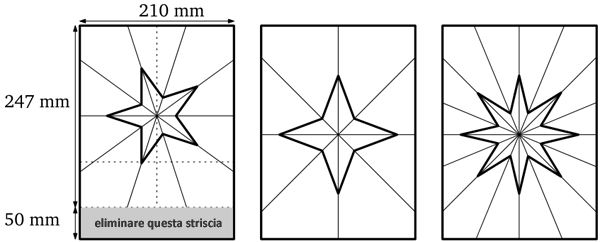
In effetti basta dire che il rapporto delle due dimensioni del rettangolo deve essere 0,85.
Il motivo matematico, invece, lo vedremo in fondo.
La particolare scelta dei due numeri deriva da un formato di carta detto lettera, che misura 8,5 x 11 pollici. Se si usa questo tipo di fogli, basta togliere una striscia alta un pollice.
Sono almeno tre secoli che abbiamo definito il metro e nel 1961 è nato il Sistema Internazionale di misure.
Oggi, in tutto il mondo, ci sono solo tre stati che si ostinano a non adottarlo: gli USA, la Liberia e la Birmania (fonte: Wikipedia).
Per favore, basta con i pollici!
Prendi allora un classico foglio da fotocopiatrice, formato A4 (210 x 297 mm) e accorcialo tagliando via una striscia alta 5 cm (50 x 210 mm).
Hai così un foglio che misura 210 x 247 mm.
Il rapporto delle dimensioni è circa quello desiderato:
8,5 : 10 = 0,85
210 : 247 = 0,850202...

Nelle successive figure:
Piega il foglio a metà parallelamente al lato più corto.

Piega di nuovo a metà nello stesso senso e apri la seconda piega.
 .
.
Piega a metà nel senso perpendicolare alle pieghe già fatte.
Ora viene la parte più delicata: quella che forma un angolo di 36°.
Osserva la figura.
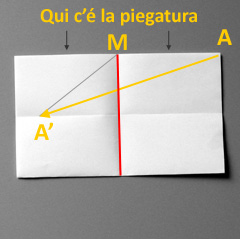

Piega il foglio (che è già piegato ametà) in modo da portare il punto A nel punto A'.
Dove si trova il punto A'?
Si trova sulla piega orizzontale che divide il foglio a metà nel punto tale che MA = MA'
In pratica si trova facendo ruotare il raggio MA attorno al centro M.
Piega come indicato nei successivi due passaggi.


Ora è il momento di tagliare.

 .
.
Questo è il risultato finale.
 .
.
Questo è lo schema delle piegature.
La stella risulta divisa a metà lungo un asse di simmetria.
La mezza stella è quindi divisa in 5 settori ampi 36°.
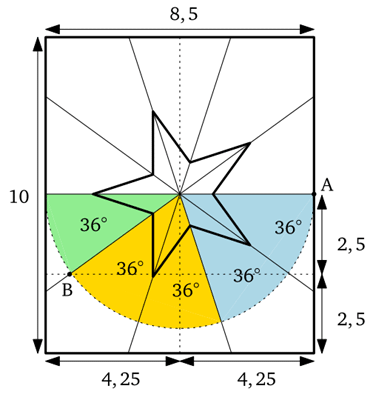
Come si fa a ottenere un angolo di 36°?
Tutto dipende dalle dimensioni del foglio!
Osserva una striscia di 8,5 x 2,5 unità.
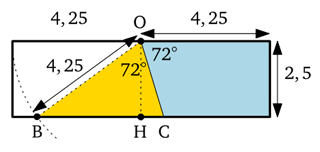
Con le piegature proposte, si viene a formare il triangolo rettangolo OBH che ha:
Quindi si può scrivere la seguente equazione:
sin(OBH) = 2,5/4,25 = 0,5882...
da cui:
OBH = 36,03°
Da cui derivano tutti gli altri angoli.
Il metodo che vi ho presentato fa storcere il naso all'origamista e non soddisfa pienamente il matematico perché usa il righello per compiere delle misurazioni che portano a una soluzione approssimativa.
Sarebbe più bella una soluzione basata su una costruzione geometrica indipendente dalle misure del foglio.
A questo proposito riporto qui di seguito il suggerimento di Francesco Silvestri.
In merito al tuo articolo "piega e taglia una stella a 5 punte" volevo segnalarti che una buona approssimazione del rapporto 0,85 si può ottenere sottraendo al lato maggiore di un foglio standard A4 un quarto del lato minore ottenendo così un rettangolo di 210 X 244,5 (il cui rapporto risulta 0,8588...) provandolo a fare e considerando quel minimo di errore dovuto allo spessore del foglio una volta che lo vai a piegare il risultato è soddisfacente...
Grazie Francesco!
Lancio agli origamisti una ulteriore sfida: partendo da un foglio quadrato è possibile, con i metodi dell'origami e un taglio unico, ottenere la classica stella a 5 punte?
Data creazione: luglio 2011
Ultimo aggiornamento: novembre 2011
xhtml 1.1
Sito Web realizzato da Gianfranco Bo