Il teorema di Steiner-Lehmus

Se in un triangolo due bisettrici sono uguali allora il triangolo è isoscele

Sono più che certo che una dimostrazione puramente sintetica (quindi Euclidea) debba esistere per questo teorema che è l'inverso del teorema sulle bisettrici di un triangolo isoscele.

Dei colleghi mi hanno proposto già una dimostrazione trigonometrica, ma a me non interessa una soluzione che non sia di tipo euclideo: per me il teorema fa parte di quella geometria e DEVE esserci una tale soluzione. Chiedo, per questo, l'aiuto degli amici di Base5 ai quali giunge già il mio ringraziamento. Questo l'enunciato del teorema.

Se in un triangolo le bisettrici degli angoli alla base sono congruenti, allora il triangolo è isoscele.

Il teorema di Steiner-Lehmus è proprio l'ultimo dei teoremi inversi:
Se in un triangolo due bisettrici sono uguali allora il triangolo è isoscele.

Nota: il teorema di Steiner-Lehmus è sempre dimostrato per assurdo. John Horton Conway ha (avrebbe?) dimostrato che questo teorema non può avere una dimostrazione diretta.
E' una sfida?
O è l'ineluttabile realtà?

Note storiche:
Daniel Christian Ludolf Lehmus, matematico tedesco, (1780-1863).
Jakob Steiner, il mitico geometra svizzero (1796-1863) imparò a leggere e a scrivere a 14 anni e iniziò a frequentare la scuola a 18 anni.

Nella "Cronologia della Matematica ricreativa" di David Singmaster si trova la seguente nota:
"1840 - Lehmus poses Steiner-Lehmus Theorem to Steiner."

"Un problema del genere, sul quale invito a riflettere, non è per niente un problema facile nonostante la formulazione sia semplicissima. Il risultato si chiama tradizionalmente Teorema di Steiner-Lehmus; la prima dimostrazione risale al 1844, dovuta a Steiner, proprio su sollecitazione di Lehmus che ne trovò un’altra nel 1850. La prima dimostrazione diretta è del 1970."
Enrico Gregorio, NOTE PER IL CORSO DI DIDATTICA DELLA MATEMATICA II, Note scritte per la SSIS Veneto, anno accademico 2004-2005.

Risposte & riflessioni

Ho trovato una dimostrazione assolutamente fulminante del teorema di Steiner-Lehmus.
Si trova nel bellissimo testo portoghese:
Introducciò a la Geometria, di Gabriel Cardona Juanals, 29 d’abril de 2004
(il file .pdf si può scaricare qui: Introduccio a la Geometria http://dmi.uib.es/~gcardona/geometria/apunts.pdf)

E' una ricostruzione della dimostrazione di Coxeter tratta da Geometry revisited, di H.S.M. Coxeter e S.L. Greitzer.

La dimostrazione si basa su due lemmi.
Lemma 1. (di normale amministrazione)
Se due corde di una circonferenza corrispondono ad angoli al centro diversi allora ad angolo maggiore corrisponde corda maggiore.

Lemma 2. (potentissimo, lo dimostro più sotto)
Se un triangolo ha due angoli diversi, allora all'angolo minore corrisponde il segmento di bisettrice maggiore.

Il teorema di Steiner-Lehmus discende direttamente dal lemma 2.
Se in un triangolo due bisettrici sono uguali allora il triangolo è isoscele.

Dimostrazione.
Supponiamo per assurdo che il triangolo non sia isoscele.
Se il triangolo ABC non è isoscele, allora i due angoli alla base B, C sono diversi, ad esempio B<C.
Ma allora, per il lemma 2, BE>CD, il che contraddice l'ipotesi.
CVD

Ora rimane da dimostrare il lemma 2 (utilizzando il lemma 1).
Lemma 2.
Se un triangolo ha due angoli diversi, allora all'angolo minore corrisponde il segmento di bisettrice maggiore

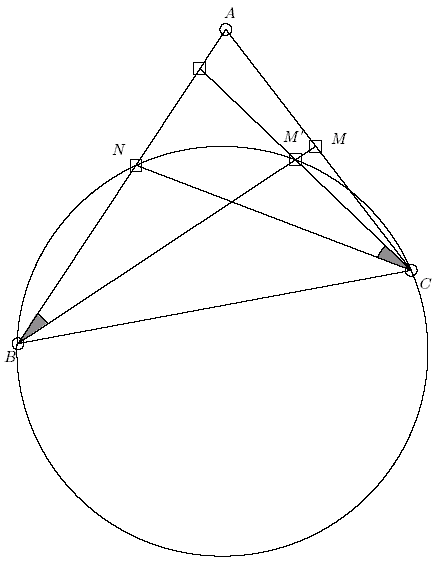
Dimostrazione.
Abbiamo il triangolo ABC con gli angoli B<C.
Tracciamo le bisettrici BM e CN.
Vogliamo dimostrare che:
BM>CN

Tracciamo il segmento CM' tale che l'angolo M'CN sia uguale alla metà dell'angolo B. M' è il punto in cui tale segmento incontra la bisettrice BM.

Si osserva che i quattro punti B, C, M, M' stanno tutti su una circonferenza. Infatti M'CN e M'BN sono angoli alla circonferenza uguali, che insistono sullo stesso arco NM'.

La corda CN corrisponde all'angolo alla circonferenza B
La corda BM' corrisponde all'angolo alla circonferenza C

> Coxeter's Introduction to Geometry discusses this theorem,
> refers to it as the Stiener-Lehmus theorem, and says there are
> over 60 proofs. He gives a simple, elegant proof of the more general
> theorem that the larger of two angle bisectors intersects the
> smaller side. The proof is independant of the parallel
> postulate, and thus is also valid in hyperbolic geometry.

I've often responded to questions about why this theorem is so hard to prove by saying that it isn't true if you allow the various lengths involved to be in more general fields, like the complex numbers. After someone asked for details about this the other day, I took the trouble to work everything out, and found to my surprise that it isn't even true when you allow them to be negative reals, which makes the situation much easier to understand.

Here's what's going on. The lengths of the A and C angle bisectors turn out to be

root{bc(a+b+c)(b+c-a)}     root{ab(a+b+c)(a+b-c)}
---------------------- and ---------------------- ,
       b+c                          a+b

Now algebraically, this does not imply that c=a, because it might be the second factor that vanishes.

However, if a,b,c are positive, then so is this second factor, and so with this assumption we CAN deduce c = a, but only by a proof that somehow distinguishes positive numbers from negative ones. Now the most common type of proof by a chain of equalities, such as:

"This length equals that length, therefore those two triangles are congruent, so this angle equals that angle, whence ... whence ultimately AB = BC."

cannot possibly do this, because it would work for all values of the variables, and it's just not possible to deduce that c=a from

The 60 proofs you mention avoid this by using order properties of the reals, typically:

"Suppose AB > BC. Then this angle exceeds that angle, whence ... whence ultimately the first angle-bisector is greater than the second. Now suppose instead that AB < BC : this implies similarly that the second is greater than the first. But we are given that they are equal, so the only possibility is that AB = BC."

We can actually smoothly vary the parameters of a triangle in such a way that one of its "edgelengths" changes sign and get a "counterexample" to the Steiner-Lehmus theorem. Here's how:

     C
    / \
   E   D
  /  I  \
 /       \
A--> F <--B

Fix C, but let A and B move freely on the x-axis. Then if
they move so as to pass right through each other:

        C
       / \
      /   \
     /     \
    /       \
<--B    F    A-->

        I


D               E

it's natural to say that c has changed sign. As they moved, the incenter I moved smoothly down, and crossed the x-axis as they passed through each other, so that it became an excenter of the final inside-out triangle.

The angle-bisector segments AD,BE,CF of the original triangle also vary smoothly during this process, and I've drawn the final positions that they get into in the above picture. Now take a = b = 1;
then the above equation for c becomes

which is satisfied by c = (-5 + root17)/2, which is about -.44 ;
then with this value of c ALL THREE of these segments are equal, but the triangle is only isosceles, not equilateral!

If there were a proof of the Steiner-Lehmus theorem of the above equality-chasing type, it would continue to work when we varied the triangle smoothly in this way, and so would prove this triangle equilateral, which it isn't. So there's no such proof!