[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Da un problema
presentato da Sprmnt21 al Siggiochi
Data una scacchiera quadrata composta da 2^n
X 2^n caselle a cui viene tolta una casella qualunque (non
necessariamente sul bordo), dimostrare che e' possibile
piastrellarla con piastrelle fatte come in figura:
![]()
Esempio:

Premessa.
La figura:
![]()
è molto nota con il nome di Tromino-L (o L-Tromino)
ed ha la seguente proprietà: con quattro Tromini-L si può
costruire un nuovo Tromino-L di dimensioni doppie.
![]()
La soluzione che propongo mostra come si può
fare una tassellazione di un quadrato di lato 2^n con UN SOLO
BUCO in un angolo.
Poi si fa migrare questo buco dove si desidera, utilizzando n
simmetrie (assiali o centrali) al massimo.
Preferisco illustrare il discorso con alcune
figure.
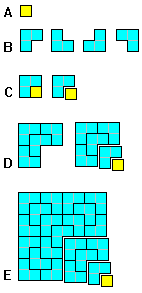
La figura A è una piastrella gialla che rappresenta il buco
nella pavimentazione.
La figura B rappresenta i nostri tasselli, chiamati anche L-tromini,
nelle quattro possibili posizioni.
La figura C mostra in come un L-tromino può essere unito
alla piastrella gialla in modo da formare un quadrato.
Il lato del quadrato è 2*2
Il L-tromino è uno gnomon del quadratino
giallo, cioè è una fgura che unita al quadrato dà un
quadrato più grande.
La figura D mostra in che modo 4 L-tromini possono essere
uniti in modo da formare un L-tromino simile al precedente ma
di dimensioni doppie.
Inoltre si può facilmente notare che questo L-tromino più
grande è uno gnomon del quadrato con la piatrella gialla e,
unito ad esso, forma un quadrato di dimensioni doppie e cioè
4*4
Questa procedura può essere ripetuta a piacere, come mostra
ad esempio la figura E.
In pratica con 4 L-tromini di qualunque dimensione si può
ottenere un L-tromino di dimensioni doppie.
Unendo questo L-tromino a quelli precedenti, ogni volta si
ottiene un quadrato di area quadrupla del precedente.
In questo modo mi sembra dimostrato costruttivamente come
ottenere un qualunque quadrato (con una piastrella gialla in
un angolo) di lato 2^n ( vedi figura F).
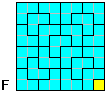
A questo punto, applicando una tecnica di
"migrazione del buco", si può traferire la
piastrella gialla in qualunque punto della tassellazione
quadrata.
La tecnica di "migrazione del buco" può essere
semplificata ricorrendo alle simmetrie assiali e centrali.
Osserviamo ad esempio la figura G.
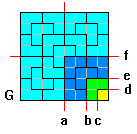
La piastrella gialla può essere trasportata
in qualunque punto del quadrato grande con soli tre colpi di
simmetria
Vediamo:
Prima simmetria: prendiamo il quadrato (verde + giallo). Con
una simmetria a scelta rispetto all'asse c, all'asse d o al
centro, è possibile spostare la piastrella gialla in uno
qualunque dei quadratini verdi.
Seconda simmetria: prendiamo il quadrato (blu + verde +
giallo). Con una simmetria a scelta rispetto all'asse b,
all'asse e o al centro, è possibile spostare la piastrella
gialla da un posto appropriato nel quadrato (verde + giallo)
in uno qualunque dei quadratini blu.
Terza simmetria: prendiamo il quadrato (celeste + blu + verde
+ giallo). Con una simmetria a scelta rispetto all'asse a,
all'asse f o al centro, è possibile spostare la piastrella
gialla da un posto appropriato nel quadrato (blu + verde +
giallo) in uno qualunque dei quadratini celesti.
Naturalmente le simmetrie vanno fatte NON rispetto al
quadrato grande ma rispetto al quadrato più piccolo di volta
in volta preso in considerazione. Estendendo questo
caso credo che si possa concludere che: se il quadrato grande
ha lato 2^n allora si può spostare il quadratino giallo
da un angolo a qualunque altro punto in n simmetrie al
massimo.
Ad esempio:

Per passare dalla situazione F alla situazione qui sotto...

E' sufficiente operare così:

1 - originale
2 - simmetria assiale del quadrato verde-giallo rispetto
all'asse c
3 - simmetria assiale del quadrato blu-verde-giallo rispetto
all'asse e
4 - simmetria del quadrato celeste-blu-verde-giallo rispetto
al centro

Sito Web realizzato da Gianfranco Bo