[HOME - BASE Cinque - Appunti di Matematica ricreativa]
I caleidocicli
Questa pagina è stata
realizzata con la collaborazione degli alunni Karim K.,
Leonardo M., Matteo S., Matteo P., Matteo R., Andrea G.,
della Scuola Media di Cogorno, classi 2° D, 3° D.
Oggi vi presento i caleidocicli.
Qui a fianco ne potete vedere due esemplari: il
caleidociclo quadrato e quello esagonale.
Sono figure straordinarie costituite da una catena di
tetraedri chiusa ad anello.
L'anello può essere fatto girare infinite volte
attraverso il suo centro.Perché si chiamano caleidocicli?
Il termine deriva dal greco:
kalòs = bello
eidos = figura
ciclos = cerchio, anello
I caleidocicli si costruiscono piegando e incollando
opportunamente un foglio di carta lungo le linee di un
reticolo triangolare.
Il capostipite di questi reticoli e l'IsoAxis,
un reticolo ideato dal grafico e disegnatore statunitense
Wallace Walker, nel 1958.
L'IsoAxis originale è formato da 60 triangoli
rettangoli isosceli.
Se volete approfondire l'argomento, vi consiglio un
bellissimo libro che unisce alla matematica dei
caleidocicli il fascino dei disegni di Esher:
Doris Schattschneider e Wallace Walker
M.C. Escher Caleidocicli
Evergreen Taschen - Germany
(è in italiano e si trova in Italia)
|
 
Caleidociclo quadrato e caleidociclo
esagonale
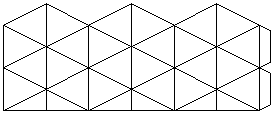
Reticolo del caleidociclo esagonale
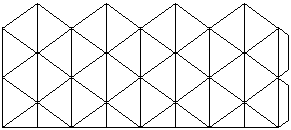
Reticolo del caleidociclo quadrato
|
Come costruire un caleidociclo
esagonale
| Fotocopiate su un cartoncino
leggero lo schema del caleidociclo esagonale (riportato
più sotto). La fotocopia dovrebbe essere ingrandita in
modo tale da occupare un foglio A4 o anche un po' più
grande.
Noi abbiamo riciclato una cartellina lunga circa 35 cm.
Ritagliate con precisione lungo il contorno.
|
 |
| Ora bisogna piegare lungo
tutte le linee. Le piegature devono essere nette e
precise.
Si comincia con le linee orizzontali.
Queste devono essere piegate due volte: prima nel
verso indicato in figura e poi nel verso opposto.
Questo perché la piegatura deve essere verso
l'interno.
|
 |
| Si continua piegando il
cartoncino lungo tutte le linee oblique. |
 |
| A questo punto, manipolando
con abilità e delicatezza, si inizia a chiudere "a
tubo" il cartoncino. Bisogna però seguire le
piegature in modo da formare una catena di 6 tetraedri.
I tetraedri sono delle piramidi a 4 facce triangolari.
|
 |
| Ecco il risultato che si
deve ottenere. |
 |
| Sempre con una manipolazione
abile e delicata si chiude ad anello la catena dei
tetraedri in modo che le linguette del primo tetraedro
vadano ad inserirsi nell'apertura dell'ultimo. Le
linguette devono essere cosparse di colla sulla
superficie esterna.
|
 |
| Dopo aver incollato le
linguette, si dovrebbe ottenere questo risultato. Che
cosa ha di speciale questa forma geometrica?
Con una leggera pressione si può far ruotare l'anello
attraverso il suo centro infinite volte, procedendo
sempre nello stesso verso.
Il caleidociclo quadrato si ottiene con la stessa
procedura, con la differenza che i tetraedri sono otto
anziché sei.
|
 |
Per mostrare come funziona il caleidociclo ci
vorrebbe un videoclip, ma siccome è troppo pesante ci siamo
limitati a inserire questa sequenza di fotografie.
Risposte
& riflessioni
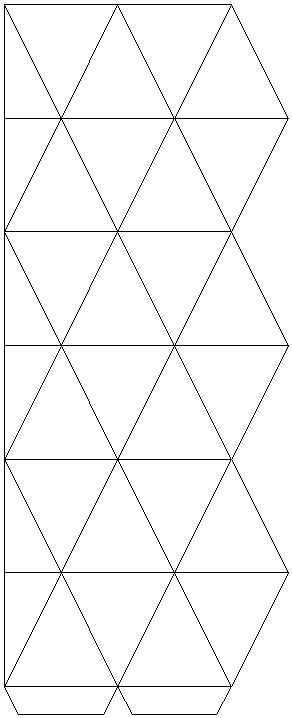
Schema del caleidocliclo esagonale
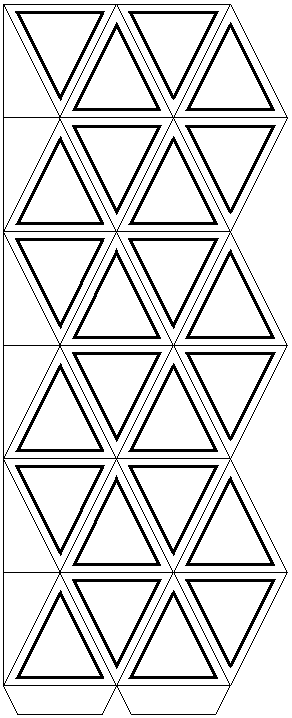
Schema del caleidocliclo esagonale
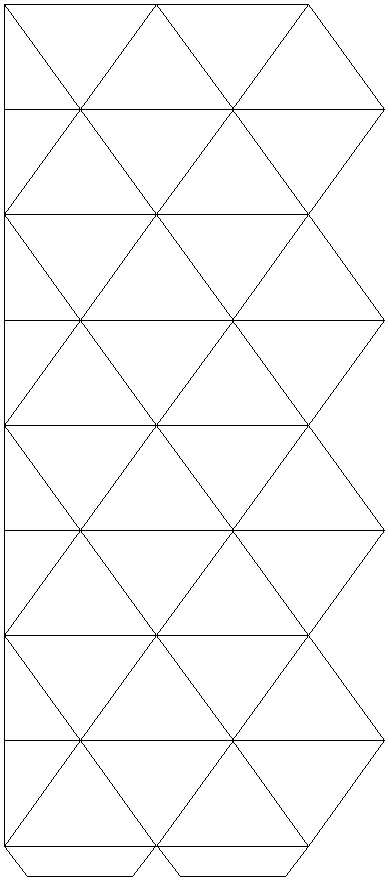
Schema del caleidocliclo quadrato
Novembre 2003
Sito Web realizzato da Gianfranco
Bo

















