[BASE Cinque - Appunti di Matematica ricreativa]
La risposta di John Horton Conway
In geometria solida il cubo camuso (che significa: cubo al quale sono stati smussati alcuni vertici) è uno dei tredici poliedri archimedei.
Il cubo camuso, o cubo simo o snub cube ha:
Si tratta di un poliedro chirale: non è equivalente alla sua immagine riflessa, e si presenta quindi in due forme distinte.

Le due forme del cubo camuso
Il cubo camuso si può ottenere dal cubottaedro come illustrato nella figura seguente.
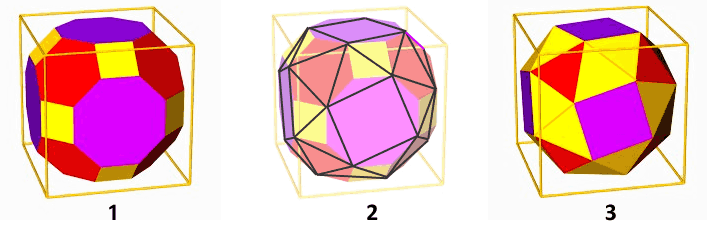
1) Si tronca un cubo ottenendo un cubottaedro.
2-3) Si tronca il cubottaedro ottenendo un cubo camuso.
Estraggo alcune linee da una lunga ed esauriente risposta data John Horton Conway su Mathforum, nel 1994
I have now looked up the OED, which has been updated so as to include this use of "snub".
Its first reference is to a 1934 paper by Coxeter, who says that "snub" is a free translation of Kepler's latin word "simus", meaning "squashed".
So it is indeed the same use as in "snub nosed".
John Conway
Ho consultato l'Oxford English Dictionary, il quale è stato aggiornato in modo da includere questo uso del termine "camuso".
Il suo primo riferimento è a un documento del 1934 di Coxeter, che dice che "camuso" è una libera traduzione della parola latina "simus" usata da Keplero, che significa "schiacciato".
Ha lo stesso significato in "naso camuso".
John Conway
Note.
Solidi archimedei.
Un solido archimedeo o semiregolare è un poliedro convesso che soddisfa le proprietà seguenti:
Un solido archimedeo ha almeno due tipi di facce distinte: i solidi che soddisfano le prime due ipotesi e che hanno solo un tipo di faccia sono proprio i solidi platonici (o regolari).
I solidi archimedei sono quindi in un certo senso i solidi più "regolari" dopo quelli platonici (da cui la dicitura "semiregolare").
Prismi e antiprismi non sono tradizionalmente ritenuti archimedei, benché soddisfino le prime due ipotesi.
Prismi e antiprismi si differenziano qualitativamente dai solidi archimedei per due fattori:
(http://it.wikipedia.org/wiki/Solido_archimedeo)
La risposta completa di John Horton Conway (in tre interventi).
Posted: Jan 8, 1994 4:00 PM
I have now looked up the OED, which has been updated so as to include this use of "snub". Its first reference is to a 1934 paper by Coxeter, who says that "snub" is a free translation of Kepler's latin word "simus", meaning "squashed". So it is indeed the same use as in "snub nosed".
I now am doubting my assertion that this use is about 150 years old, which was based on my memory of finding these names in some book of about that vintage; maybe I just found the names for the polyhedra other than the snubs? Anyway, I withdraw that assertion until I've hunted around some more.
I summarize the principles used in naming the Platonic and Archimedean polyhedra:
1) The Platonic and rhombic polyhedra are named from the numbers of their faces.
2) From the P-hedron we obtain the truncated P-hedron by cutting of the corners so as not to reduce the edges to points, and from either the P-hedron or its dual Q-hedron we obtain the PQ-hedron by "complete" truncation, which does reduce the edges to points.
3) The snub P-hedron is the convex hull of the set of points obtained from the P-hedron by shrinking each face into its plane, and rotating slightly.
----------------------
From 1) we get the
tetrahedron, hexahedron(=cube), octahedron, dodecahedron, icosahedron,
rhombic dodecahedron, rhombic triacontahedron
From 2) the truncated tetrahedron, cube, octahedron, dodecahedron, icosahedron, cuboctahedron, icosidodecahedron, and the
cuboctahedron (from either cube or octahedron) icosidodecahedron (........ icosa or dodeca) rhombicuboctahedron ( ... rhombic dodeca or cubocta) rhombicosidodecahedron (... rhombic triaconta or icosidodeca)
From 3) we get the
snube cube ( = snub octahedron)
snub dodecahedron ( = snub icosahedron)
---------------------------
All these names come originally from Kepler.
I remark that the basic names are from Greek stems:
mono, di, tri, tetra, penta, hexa, hepta, octa, ennea, deca,
undeca, dodeca, triskaideca, tetrakaideca, ... icosa,
..... icositetra, ... triconta, ... hexaconta, ... enneaconta, ...
(for 24 30 60 90)
all appear in names of well-known polyhedra.
The stem "hedron" really means "seat", and is indeed cognate with that English word, "h" in Greek often corresponding to "s" (compare "hepta" with "septa") and "d" to "t". One other English word deriving from the same root is "cathedral" : a "cathedral church" is one that contains a bishop's chair, whose name derives from "cata" meaning "down", and "hedron" meaning "seat", since it's the seat from which the bishop hands down his authoritative opinions.
JHC
Posted: Jan 8, 1994 4:01 PM
This question has also interested me for quite some time. In general, the names for the Archimedean solids stem from Kepler's latin versions, as follows:
tetrahedron, hexahedron=cube, octahedron, dodecahedron, icosahedron
from the numbers of faces.
then the truncated versions of these, obtained by "cutting off the corners", so as to leave parts of all the original edges.
then the cuboctahedron and icosidodecahedron, obtained by truncations that reduce all the original edges to zero length, are given these names because the cuboctahedron, for instance, is the intersection of a cube and an octahedron.
The duals of these two solids are the rhombic dodecahedron and rhombic triacontahedron, named after the number and shape of their faces.
Now come the truncated cuboctahedron and truncated icosidodecahedron, in the traditional scheme, which some people have tried to rename as decribed below.
Now just as we obtain the cuboctahedron by complete truncation of either the cube or the octahedron, we can obtain a certain solid by complete truncstion of either the rhombic dodecahedron or the cuboctahedron. This solid is the rhombicuboctahedron, in which the "rhombi" is really an abbreviation for "rhombic dodecahedron". The rhombicosidodecahedron arises in a similar way.
If on truncates a cuboctahedron, the four-sided faces are rectangles rather than squares, so some people dislike using the name "truncated cuboctahedron" for the Archimedean polyhedron in which they are squares. They therefore call this the "great rhombicuboctahedron", and use "small rhombicuboctahedron" for what is traditionally called just the rhombicuboctahedron. In my view, this is misguided, because it loses the meaning of rhombicuboctahedron as just an instance of the "PQhedron" that is obtainable by complete truncation of either the Phedron or the Qhedron, and just treats it as a meaningless name. We do better by understanding that the names really name only up to combinatorial equivalence.
This leaves only the "snub cube" and "snub dodecahedron" unexplained. I once tried to find who first used these names in English, but without success. I was surprised to find that the Oxford English Dictionary does not mention this use of "snub", although it is about 150 years old at least. I presume that it is just an instance of the ordinary English word "snub" meaning something like "rounded", as in "snub-nosed".
When I've finished reading my email, I'll look in the on-line OED which by now might have this use recorded.
JHC
Posted: Apr 21, 1994 2:51 PM
Kepler called this figure a "cubus simus", where the Latin word "simus" means something like "squashed". I think it was Coxeter who first translated "simus" into "snub" (in a paper published around 1930).
John Conway
Data creazione: dicembre 2011
Ultimo aggiornamento: dicembre 2011
xhtml 1.1
Sito Web realizzato da Gianfranco Bo