[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Il paradosso del principe Rupert

1. Passare attraverso un foglio di carta
Nessuno vi crederà quando vi vanterete di essere capaci di fare un buco in un foglio di carta formato A4 (21 x 29,7 cm), abbastanza grande da passarvi attraverso.
Potete scommetterci, la vittoria sarà vostra.
Se l'interlocutore esita ad accettare la scommessa, ditegli pure che siete disposti anche a passare attraverso una cartolina postale.
Come?

2. Il flauto è troppo lungo
Alice abita nel Paese dei Pignoli. In questo paese i pacchi postali devono avere forma di parallelepipedo rettangolo e le loro dimensioni non devono superare la lunghezza di 60 cm.
Alice deve spedire ad un suo amico un flauto indiano lungo un metro.
Prepara un bel pacco che misura 10x10x103 cm e lo consegna all'ufficio postale, sperando di farla franca.
Niente da fare! Il pacco le viene immediatamente restituito perché supera le dimensioni consentite.
Alice torna a casa e, dopo averci pensato un po' su, impacchetta il flauto in un modo diverso.
L'indomani si presenta all'ufficio postale dove il pacco viene accettato senza problemi.
E' opportuno precisare che il flauto è in un pezzo unico di robusta canna di bambù e Alice non ha commesso l'orrendo delitto di tagliarlo nè di piegarlo.
Come ha fatto?

3. La più grande cartolina che si può spedire
Una cassetta postale ha la forma di un cubo il cui lato interno è lungo 1 metro.
Quali sono le dimensioni (lunghezza e larghezza) della più grande cartolina che può esservi contenuta senza arrotolarla né piegarla?
Per "cartolina" si intende un cartoncino quadrato.
Trascurare lo spessore della cartolina.

4. Il problema del principe Rupert
Il problema 1, "Passare attraverso un foglio di carta", si risolve con un onestissimo trucco, ma quello che vi presento ora è un sano problema di geometria, senza trucco e senza inganno. E' conosciuto con il nome di problema del principe Rupert.
E' possibile praticare un foro in un cubo, tale che vi possa passare attraverso un altro cubo uguale al primo o addirittura più grande?
Due suggerimenti doverosi: la risposta è sì, e il foro non è cilindrico.
Ma come si fa?

Nota storica
John Wallis. Perforatio cubi, alterum ipsi aequalem recipiens. (De Algebra Tractatus. Chap. 109) = Opera Mathematica, vol. II, Oxford, 1693, pp. 470-471, ??NYS. Cites Rupert as the source of the equal cube version. (Latin and English in Schrek.)

Ozanam-Montucla. 1778. Percer un cube d'une ouverture, par laquelle peut paffer un autre cube égal au premier. Prob. 30 & fig. 53, plate 7, 1778: 319-320; 1803: 315-316; 1814: 268-269. Prob. 29, 1840: 137. Equal cubes with diagonal movement.

U. Graf. Die Durchbohrung eines Würfels mit einem Würfel. Zeitschrift math. naturwiss. Unterricht 72 (1941) 117. Nice photos of a model made at the Technische Hochschule Danzig. Larger and better versions of the same photos can be found in: W. Lietzmann & U. Graf; Mathematik in Erziehung und Unterricht; Quelle & Meyer, Leipzig, 1941, vol. 2, plate 3, opp. p. 168, but I can't find any associated text for it.

W. A. Bagley. Puzzle Pie. Op. cit. in 5.D.5. 1944. No. 12: Curios [sic] cubes, p. 14. First says it can be done with equal cubes and then a larger can pass through a smaller. Claims that the larger cube can be about 1.1, but this is due to an error _ he thinks the hexagon has the same diameter as the cube itself

(prof. David Singmaster)

Risposte & riflessioni

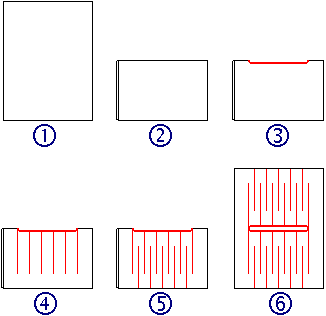
1. Passare attraverso un foglio di carta
Ecco come potete centellinarvi la vittoria.

Seguite l'illustrazione. Le linee rosse indicano i tagli che dovete effettuare utilizzando un paio di forbici.

  1. Prendete un foglio di formato A4.
  2. Piegatelo a metà
  3. Tagliatene un pezzo come indicato in figura 3. In questo modo avrete praticato una sottile fessura. Aprite il foglio e chiedete al vostro intelocutore di passare attraverso la fessura. Egli penserà subito di aver vinto la scommessa.
  4. Ditegli che proverete ad allargare la fessura. Richiudete il foglio e praticate i tagli come indicato in figura 4. Riaprite il foglio. Il vostro foro sarà sfrangiato e più grande di prima, ma non ancora grande abbastanza da potervi passare una persona. Ancora una volta il vostro interlocutore crederà di avere la vittoria in pugno.
  5. Chiedetegli un'ultima possibilità: proverete ad allargare il foro ancora un po'. Richiudete il foglio e praticate i tagli come indicato in figura 5.
  6. Ora riaprite il foglio delicatamente e aprite il foro. Si formerà una grande circonferenza costituita da una striscia di carta a zig-zag.

Maggiore è il numero dei tagli e più lunga è la circonferenza che si ottiene. Vi conviene fare alcune prove prima di lanciarvi nelle scommesse.
Lavorando con molta delicatezza, è possibile passare anche attraverso un foglio grande come una cartolina!

2. Il flauto è troppo lungo
Tutti sanno che la diagonale del cubo è uguale al lato moltiplicato per la radice quadrata di 3 ma a nessuno viene in mente di spedire un flauto lungo 1 m in una scatola cubica di lato 60 cm.

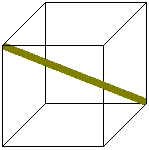
lato: l = 60 cm

diagonale: d = 60 radq(3) = 103,... cm

3. La più grande cartolina che si può spedire
La seguente figura illustra la risposta.

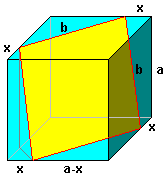
Ammettiamo che i vertici della cartolina (quadrato giallo) debbano trovarsi sugli spigoli del cubo come illustrato nella fgura. (n.b. non ho la dimostrazione del perché)
A questo punto è facile trovare il valore di x per il quale la cartolina abbia i lati uguali, condizione necessaria ma non sufficiente affinché sia un quadrato.
Grazie a Pitagora...

b2 = a2 + 2x2 = (a-x)2 + (a-x)2

da cui si ricava incredibilmente:

x = a/4

Trovato ciò, si può calcolare il valore di b in funzione di a

b = radq(9/8a2) = 1,06...a

Si nota subito che: b > a, sia pur di poco.

Ehi, ehi, resta da dimostrare che la cartolina ha gli angoli retti.

4. Il problema del principe Rupert
Se avete risolto il problema della cartolina, in pratica, avete risolto anche il problema del principe Rupert.
Si tratta di fare un foro di sezione quadrata grande come la cartolina e perpendicolare alla cartolina stessa.
Del cubo forato rimane ben poco, ma il paradosso è risolto.
Sembra che qualcuno lo abbia realizzato materialmente e che abbia anche fotografato l'opera.

Sito Web realizzato da Gianfranco Bo