
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Un poliedro topologicamente equivalente al toro dimostra il teorema dei 7 colori
Ma quanti figli aveva il re?
Nel 1840 August Moebius pose il seguente problema sotto forma di
favola:
"C'era una volta un re che aveva cinque figli. Egli stabilì che alla sua morte il regno fosse suddiviso tra i figli in cinque regioni in modo che ciascuna regione confinasse con le altre quattro. E' possibile esaudire la sua richiesta?"
Questa è la storia originale di Moebius.
Ma il re visse ancora a lungo ed ebbe un altro figlio.
E' possibile dividere il regno in 6 regioni in modo che ciascuna di esse abbia
almeno una linea di confine con ciascuna delle altre 5?
Il matematico ungherese Lajos Szilassi, nel 1977, scoprì che il che
il re ebbe un settimo figlio.
A questi punti, il problema diventa veramente difficile.
E' possibile dividere il regno in 7 regioni in modo che ciascuna di esse abbia
almeno una linea di confine con ciascuna delle altre 6?
Ora mi è venuto un dubbio...
E se i figli fossero stati 8?
Ultimo aggiornamento: gennaio 2006
Su un anello (o nastro) di Moebius è possibile dividere il regno in 5 oppure 6 regioni in modo che ciascuna di esse abbia almeno una linea di confine con tutte le altre.
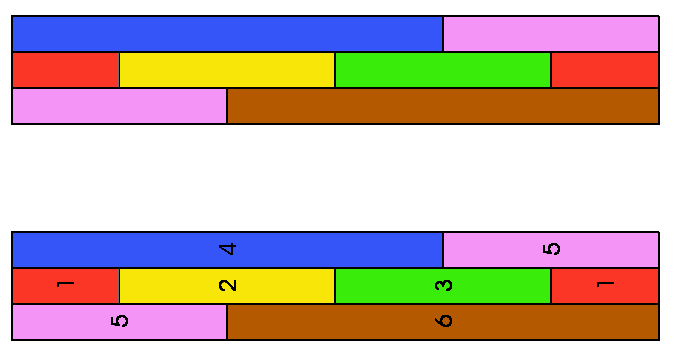
Potete verificarlo voi stessi preparando una striscia di carta esattamente come illustrato nella figura qui sotto. La striscia è divisa in cinque regioni numerate da 1 a 5 e colorate con cinque colori diversi. Ciascuna regione è colorata dello stesso colore e porta lo stesso numero sia sul "diritto" che sul "rovescio".

Formate poi un anello di Moebius con la striscia colorata. Dopo aver dato mezza torsione, i lati A e B saranno uniti rispettivamente ai lati A' e B'. Esaminando attentamente l'anello potrete constatare che ogni regione confina con tutte le altre.

Il problema si sarebbe potuto risolvere anche se il re avesse avuto sei figli. Infatti per l'anello di Moebius è stato dimostrato il teorema dei 6 colori: 6 colori sono sufficienti per colorare qualsiasi mappa su un anello di Moebius.
Ecco una striscia a sei colori che risolve il problema.
Su un toro possibile dividere il regno in 7 regioni in modo che ciascuna di esse abbia almeno una linea di confine con ciascuna delle altre 6.
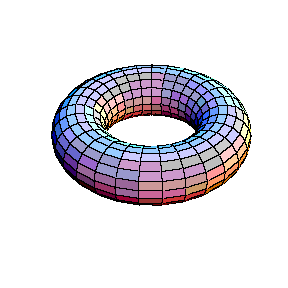 |
 |
| toro | mappa a 7 colori sul toro |
E la migliore dimostrazione di questo fatto è il poliedro di
Szilassi: un poliedro formato da 7 facce, ciascuna delle quali ha un lato in
comune con ciascuna delle altre.
E tale poliedro è equivalente ad un toro.
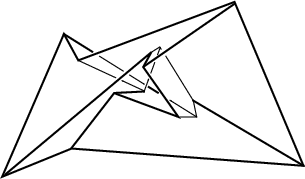
Il poliedro di Szilassi
 |
 |
 |
Alcune viste del poliedro di Szilassi

Le 7 facce esagonali del poliedro di Szilassi
colorate con i tradizionali 7 colori dell'arcobaleno.
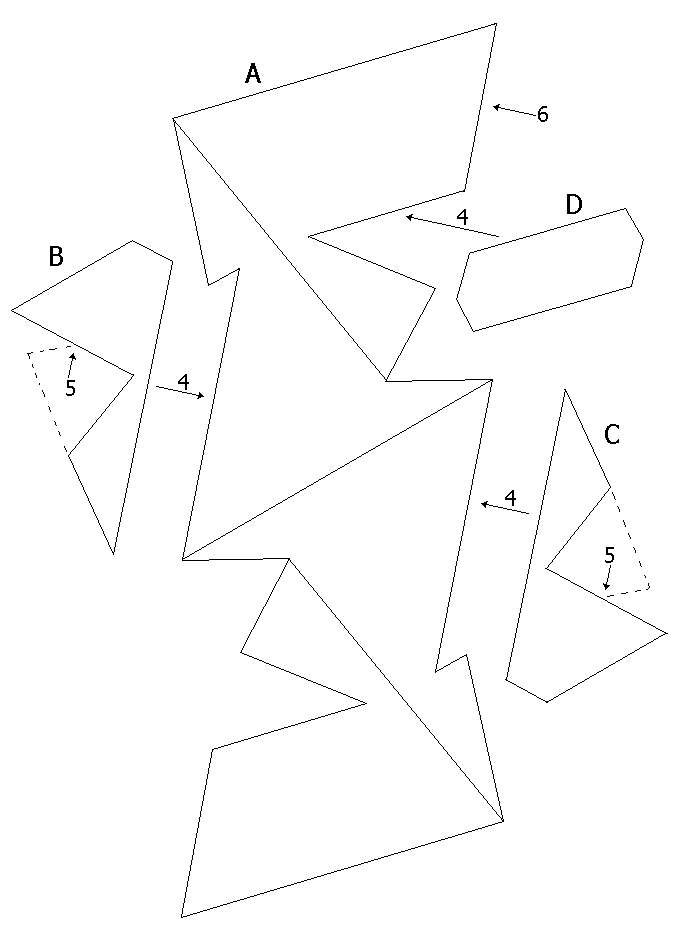
Volete costruire un poliedro di Szilassi?
Utilizzate questo modello.
Se i figli fossero stati 8, il regno avrebbe dovuto avere la
forma di bi-toro
Bi-toro: (4x2(1-x2)-y2)2+z2-0.25
= 0

bi-toro o doppio toro
E se i figli fossero stati 9?
Ora basta, dài!
Sito Web realizzato da Gianfranco Bo