
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Alla ricerca di un modello quasi-piano
Erone afferma che Dionisodoro
scrisse un'opera intitolata "Sul Toro" nella quale si
trova una formila per calcolare il volume del toro.
Arthur Cayley us˛ il termine "torus" nel 1870.

Un toro, in teoria, si potrebbe ottenere
da un rettangolo di carta
1. Si prende un rettangolo di carta

2. Si piega a tubo e si incollano i bordi.

3. Si curva il tubo in modo da formare un cerchio e si incollano le estremitÓ. Beh, questo non Ŕ facile da farsi con un tubo di carta!
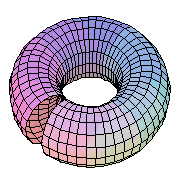
4. Il toro Ŕ terminato.

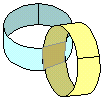
Un modello di toro facilmente
realizzabile ma poco pratico
Si incollano due strisce di carta in modo da formare una croce.
Con le due strisce si formano due cilindri.
Un modello di toro facilmente
realizzabile e molto pratico
Si ritagliano due rettangoli di carta e si incollano come
illustrato nella figura.
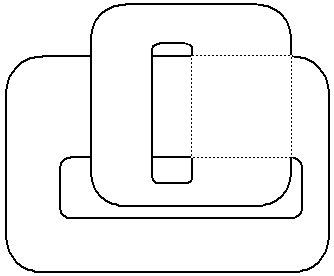
Questo modello ha il vantaggio di essere quasi-piano.
Potete metterlo in una cartellina o in mezzo ai fogli di un
quaderno.
Ma ha anche altri vantaggi. Ad esempio su questo modello Ŕ
facilissimo dimostrare il teorema dei 7 colori sulla superficie
torica.
Si possono inoltre risolvere facilmente:
b) il problema delle 3 utilities (gas, luce, acqua) sulla
superficie torica.
c) il problema delle 4 utilities e oltre... ma quanto oltre?
Il pi¨ semplice modello del toro
Giunti alla fine... ritorniamo all'inizio.
Il pi¨ semplice modello piano del toro Ŕ un rettangolo. Si deve
ricordare che i lati opposti coincidono e sono nello stesso
verso, quindi una linea che "esce" da un lato "rientra"
dal lato opposto esattamente nella stessa posizione e con la
stessa inclinazione.

giugno 2004
Sito Web realizzato da Gianfranco Bo