[BASE Cinque - Appunti di Matematica ricreativa]

Il volume della sfera

Come calcolare il volume della sfera senza versare neppure una goccia d'acqua sulla tovaglia... e senza sporcare!

Premessa

Per capire questo esperimento bisogna:

• sapere che il volume del cilindro è triplo del volume del cono avente lo stesso raggio e la stessa altezza del cilindro;
• conoscere le formule per il calcolo dei volumi del cilindro e del cono;
• conoscere le basi del calcolo letterale.

Un esperimento con tre recipienti

I recipienti che abbiamo usato si trovano nei cataloghi di materiale didattico. Il diametro della sfera è circa 10 cm. Noi abbiamo trovato un set di 6 solidi (cubo, parallelepipedo, piramide, cilindro, cono, sfera) ad un prezzo di circa 12 €, nel 2019.

Prendiamo tre recipienti a forma di cono, sfera, cilindro.

Tutti e tre hanno lo stesso diametro.

Inoltre il cono e il cilindro hanno il diametro uguale all'altezza.

Inseriamo la sfera nel cilindro.

Iniziamo a versare acqua nel cilindro...

Continuiamo a versare acqua fino a quando il suo livello raggiunge il bordo del cilindro.

Bisogna premere la sfera verso il basso facendo attenzione che non vi entri dell'acqua attraverso il foro.

Estraiamo la sfera dal cilindro, facendola sgocciolare per bene.

Il volume della sfera, in rapporto al volume del cilindro corrisponde alla parte del cilindro stesso rimasta vuota.

Ma quanta acqua si trova nel cilindro?

Per capirlo, versiamo l'acqua nel cono, che ha lo stesso diametro e la stessa altezza del cilindro.

L'acqua riempie il cono esattamente fino all'orlo.

Cosa possiamo concludere?

Possiamo concludere che il cono più la sfera danno il volume del cilindro.

Ma siccome sappiamo che il cono è equivalente a 1/3 del cilindro, possiamo dedurre che:

1. il volume della sfera è 2/3 del volume del cilindro;
2. il volume della sfera è doppio del volume del cono.

Come possiamo ricavare la formula del volume della sfera?

Semplice:

1. prendiamo la formula del cilindro equilatero e la moltiplichiamo per 2/3;
2. oppure prendiamo la formula del cono avente l'altezza uguale al diametro e la moltiplichiamo per 2.

Così calcoleremo il volume di una sfera che ha lo stesso raggio rispettivamente del cono o del cilindro.

Ok, facciamo la prima delle due.

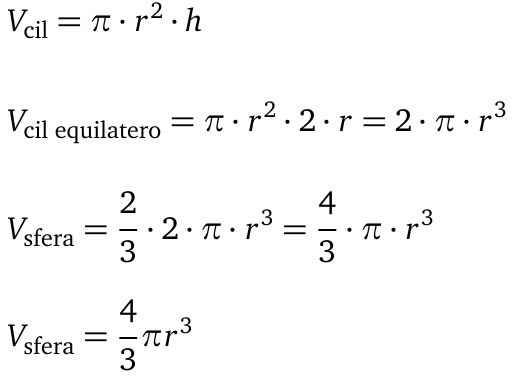
La seconda è ancora più facile e naturalmente porta allo stesso risultato.

Orrore! Questa è una formula matematica ricavata empiricamente!

E allora?

Come credete che facesse Archimede?

E i matematici di oggi?

Meraviglia!

Data creazione: maggio 2010

Ultimo aggiornamento: febbraio 2019

xhtml 1.1

Sito Web realizzato da Gianfranco Bo