[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Clessidre, orologi e calendari

1. La clessidra
La clessidra è uno strumento per la misura del tempo. E' costituita da due piccoli recipienti di vetro sovrapposti e comunicanti fra di loro attraverso uno stretto passaggio. La clessidra contiene della sabbia finissima che, scorrendo lentamente attraverso lo stretto passaggio, dà la misura del tempo trascorso.
Ecco alcuni semplici problemi con la clessidra.
Con una clessidra da 10 minuti, ad esempio è possibile misurare 10, 20, 30, 40 minuti, ... capovolgendola ogni volta che la sabbia è interamente passata da un recipiente all'altro.
Con una clessidra da 5 minuti e una da 6 minuti, come posso misurare 17 minuti?
E 1 minuto?

2. Le due clessidre
Con una clessidra da 7 minuti e una da 11 minuti, come posso misurare 15 minuti?

3. La cottura delle uova sode
Andrea Pinzimonio è un ottimo cuoco. Il suo piatto più raffinato e difficile è l'uovo sodo.
Infatti un uovo sodo perfetto deve bollire esattamente 9 minuti, e le uova sode di Andrea sono sempre perfette.
Il difficile sta nel fatto che Andrea per misurare il tempo di cottura ha a disposizione soltanto due clessidre: una da 4 minuti e una da 7 minuti.
Come può misurare 9 minuti?

4. I cubetti di ghiaccio
Mi hanno regalato un frigorifero. E' un po' antiquato, ma funziona benissimo. Ci faccio i cubetti di ghiaccio. Il freezer può contenere 7 forme per cubetti di ghiaccio, impilate l'una sull'altra. Ciascuna forma contiene 12 cubetti di ghiaccio. Purtroppo nel freezer non ci sono scaffali perciò, prima di appoggiare una forma sopra un'altra, bisogna aspettare che la prima sia ghiacciata altrimenti la forma che sta sopra si incastra in quella che sta sotto con conseguente fuoriuscita di acqua e formazione di cubetti di ghiaccio troppo piccoli.
In queste condizioni, sai dirmi qual è il metodo più veloce per fare cubetti di ghiaccio?

5. Le bistecche in padella
Théophile Gourmet è alle prese con le bistecche di vitello in padella. Deve preparare tre bistecche ma ha una padella che ne contiene solo due.
Come può fare per cuocerle nel più breve tempo possibile?
Théophile ha compiuto lunghissimi studi da cuoco e sa che una fetta di filetto da 180 g deve essere tenuta in padella 3 minuti da un lato e 3 minuti dall'altro lato.
Ovviamente la carne deve essere servita calda.
Se cuoce prima 2 fette insieme e poi la terza da sola, impiega ben 12 minuti e come risultato ha due fette fredde e una calda.
Tuttavia Théophile conosce un metodo per cuocerle in 9 minuti ottenendone due calde ed una tiepida.
Sapreste trovarlo?

6. Tre lavori, due persone
I coniugi Parodi devono realizzare tre faccende domestiche.

• Passare l'aspirapolvere al primo piano della casa. Il lavoro richiede 30 minuti e si dispone di un solo aspirapolvere.
• Potare la siepe. Questo lavoro richiede 30 minuti e si dispone di un solo paio di forbici.
• Dar da mangiare al bebé e metterlo a letto. Anche per questo lavoro sono necessari 30 minuti.

Come possono fare marito e moglie per realizzare tutto ciò nel tempo più breve possibile?

7. Quattro lavori, una persona
La signora Parodi ha un intero pomeriggio per svolgere le seguenti faccende domestiche.

• Preparare una torta: sono necessari 20 minuti per farla e 30 minuti per cuocerla al forno.
• Lavare la biancheria: sono necessari 5 minuti per metterla nella lavatrice, poi occorre aspettare 60 minuti prima che sia lavata ed infine occorrono altri 5 minuti per stenderla.
• Guardare un telefilm che dura 60 minuti.
• Stirare 3 camice e 2 pantaloni: sono necessari circa 60 minuti.

La signora Parodi tiene la lavatrice, il forno elettrico, l'asse da stiro e il televisore in cucina.
E' possibile svolgere tutte queste faccende in un'ora e mezza ore e concedersi il resto del pomeriggio per una passeggiata tra i negozi della città?

8. I quattro soldati
E' una notte buia ma non tempestosa. Però piove. Da questo lato del fiume ci sono quattro soldati in fuga, inseguiti dal feroce nemico. I quattro devono attraversare una passerella pericolante che può reggere al massimo due uomini.
Se riusciranno a passare sull'altra riva del fiume saranno salvi perché il feroce nemico è molto, molto pesante.
I quattro uomini hanno una sola lanterna, che è indispensabile perché la passerella è piena di buchi.
Questo fatto ha diverse conseguenze sulle quali è bene riflettere:

• se due uomini camminano assieme devono stare vicini e procedere alla velocità del più lento;
• inoltre uno di loro deve tornare indietro per portare la lanterna a quelli che devono ancora attraversare.

Ciascuno dei quattro uomini cammina ad una velocità diversa dagli altri:

• Andrea, campione di maratona, impiega 1 minuto ad attraversare la passerella;
• Bernardo, abile ciclista, ma veloce anche a piedi, impiega 2 minuti;
• Carlo, che si è congelato i piedi al Polo Nord, impiega 5 minuti;
• Diego, che insiste a portarsi appresso 50 litri di birra, impiega 10 minuti.

In quale ordine devono attraversare il ponte se vogliono impiegare esattamente 17 minuti?

9. L'orologio a cucù
Se impiega 5 secondi a suonare le 6, quanto impiegherà a suonare le 12?
Se impiega 6 secondi a suonare le 6, quanto impiega a suonare le 11?

10. Lancette che si sovrappongono
Tutti sanno che alle ore 12 le lancette dell'orologio sono sovrapposte.
Quante altre volte si sovrappongono nel giro di 12 ore? A quali ore?

11. Lancette perpendicolari
Tutti sanno che le lancette dell'orologio alle ore 3 sono disposte ad angolo retto.
Quante volte al giorno le lancette di un orologio formano un angolo retto?

12. Orologi mal tarati
Un orologio va avanti di un minuto ogni ora, un altro orologio rimane indietro di un minuto ogni ora. Quale differenza cè in un giorno?

13. L'orologio di Immanuel Kant
Si dice che Immanuel Kant (il famoso filosofo) era di costumi talmente regolari che gli abitanti di Konigsberg si basavano sul suo passaggio in determinati luoghi per regolare i loro orologi.
Un giorno kant ebbe la sgradevole sorpresa di trovare l'orologio di casa fermo. Il grande filosofo non poteva regolare l'orologio di casa perché il suo orologio da tasca era in riparazione dall'orologiaio e quindi egli non poteva sapere l'ora esatta.
Kant, tuttavia, mantenne la calma e andò a trovare il suo amico Schmidt, un commerciante che abitava a circa 2 km di distanza.
Entrando in casa del suo amico, vide l'ora segnata da un orologio da parete che si trovava nell'ingresso.
Dopo aver passato alcune ore chiaccherando con Schmidt, Kant tornò a casa sua percorrendo la stessa strada dell'andata con il suo passo costante e regolare che non aveva cambiato da vent'anni.
Non aveva la minima idea di quanto tempo avesse impiegato al ritorno ma, appena entrato in casa regolò il proprio orologio sull'ora esatta.

Come poteva Kant conoscere l'ora esatta?

14. L'orologiaio ubriaco
I vecchi, buoni orologi, quelli con le lancette sono sempre più rari. Per questo il mio orologiaio, deluso dagli orologi digitali, beve sempre più spesso.
Un giorno, nel quale era particolarmente bevuto, riuscì a riparare perfettamente il mio orologio ma proprio alla fine commise un errore: scambiò le lancette cioè collocò la lancetta delle ore al posto di quella dei minuti e viceversa.
Quella sera andai a ritirare il mio orologio. L'orologiaio gli diede la corda e lo regolò sull'ora esatta: erano le 18 in punto.
Ritirai, tutto soddisfatto, il mio orologio ma dopo un po' di tempo mi resi conto del disastro.
Ritornai dall'orologiaio per protestare. Egli posò il bicchiere di birra sul banco, prese il mio orologio, lo osservò attentamente e mi disse:
-Hic! Che problema c'é? Hic! Il suo orologio segna l'ora esatta! Hic!
Molto stupito guardai l'orologio. L'orologiaio non si era sbagliato!
Che ora era?

15. Gemelli che nacquero in mesi diversi
Aldo e Baldo nacquero in due giorni diversi di due mesi diversi, eppure sono gemelli.
Come si spiega?

16. Gemelli che vissero in secoli diversi
Aldo nacque, visse e morì nel XIX secolo, Baldo nacque, visse e morì nel XX secolo. Eppure Aldo e Baldo erano gemelli, ma non quelli del problema precedente.
Come si spiega?

17. Il compleanno dei gemelli
Aldo e Baldo sono due gemelli che usano invitarsi a vicenda per la festa del proprio compleanno.
Un giorno Aldo invita Baldo. Alla fine della festa Baldo fa gli auguri ad Aldo e gli dice:
Non dimenticare di venire alla festa del mio compleanno, fra due giorni.
Come si spiega?
C'è da precisare che Aldo e Baldo festeggiano il proprio compleanno nella data esatta in cui compiono gli anni.

18. Compleanno di gemelli a 10 giorni di distanza
Siamo nell'anno 1632.
Aldo e Baldo sono due gemelli, nati uno prima della mezzanotte di un giorno e l'altro dopo la mezzanotte del giorno successivo, che usano invitarsi a vicenda per la festa del proprio compleanno.
Un giorno Aldo invita Baldo. Alla fine della festa Baldo fa gli auguri ad Aldo e gli dice:
Non dimenticare di venire alla festa del mio compleanno, fra dieci giorni.
Quanti anni ha compiuto A?
Sappiate che sia A che B festeggiano il proprio compleanno nella data esatta in cui compiono gli anni.

19. Quanti anni ha Pippo
Pippo dice: "L'altro ieri avevo 33 anni e l'anno prossimo ne compirò 36. Come si spiega?

20. Il compleanno di Pippo
Pippo, alla festa del suo compleanno, nel 2000, dice: Bei tempi quelli in cui avevo n anni nell'anno n^2.
Quante candeline c'erano sulla torta di Pippo?
Suggerimento: c'erano tante candeline quanti erano gli anni compiuti da Pippo nel 2000.

21. Strani compleanni
Una persona compie 69 anni nel 96 (che significa 1996): sono le stesse cifre ma nell'ordine inverso.
La stessa persona aveva compiuto 58 anni nel 85, 47 anni nel 74 e così via.
Un'altra persona compie 79 anni nel 97, aveva compiuto 68 anni nel 86, 57 anni nel 75 e così via.
Non a tutte le persone capita questa coincidenza.
Qual è la condizione perché si verifichi?

22. Quanti anni ha Lucia?
Lucia, oggi ha il triplo dell'età di Monica (in anni). Fra tre anni Lucia avrà il doppio dell'età di Monica.
Quanti anni hanno Lucia e Monica?

23. Orologio digitale
Un orologio digitale segna le ore e i minuti dalle 0:00 alle 23:59. Quante volte in un giorno sul quadrante dell'orologio compaiono tutte le cifre uguali?

24. Trionfi dell' Inter
(inviato al Forum da Supertifoso, 17/06/04 12:15 )
Ho chiesto all'oracolo di Mara Dona quando l' Inter vincerà qualcosa.
Il vecchio saggio è caduto in trance - fumando una polvere di funghi allucinogeni - e ha sentenziato:
"La notizia cattiva è che l' Inter vincerà qualcosa alle ore ab del giorno cd del mese ef dell' anno ghil"
"Che cavolo di risposta è?" ho commentato.
"Ad ogni lettera corrisponde una cifra da 0 a 9" ha risposto
"Ma ci sono una marea di possibilità" ho protestato
"La notizia buona è che, fra tutte le possibilità, si verificherà quella più prossima"
Fatelo sapere a Moratti, io non ho il coraggio.

25. Quando avrai la mia età
Io ho il doppio dell'età che tu avevi quando io avevo la tua età.
Sapendo che quando tu avrai la mia età, insieme avremo 90 anni, quanti anni abbiamo?

26. L'orologio stregato
(Inviato al Forum da Ronfo, 22/06/04 8:30)
Si racconta che dalle parti di Zurigo ci sia un orologio stregato.
Il fatto di per se ha ben poco di misterioso ma si sa che molte storie vengono ammannite ai turisti per rendere più caratteristico il luogo di villeggiatura .
In breve sul campanile di una chiesa alle sei precise del mattino fu fatto partire un orologio , purtroppo le lancette furono montate sui perni sbagliati per cui quella delle ore partì di gran carriera mentre quella dei minuti prese un'andatura da tartaruga.
Quando le stramberie dell'orologio furono descritte all'orologiaio vecchio e malato egli volle a tutti i costi essere trasportato nel suo lettuccio per osservare lo strano fenomeno; ma per una incredibile coincidenza quando arrivò sul posto l'orologio segnava l'ora esatta , il vecchio fu così colpito dal fatto che morì di contentezza ; per questo fatto si pensò che l'orologio fosse stregato.
Ecco il problema : se l'orologio parte alle sei esatte con le lancette invertite a che ora esse raggiungeranno una posizione che indichi l'ora esatta?

Risposte & riflessioni

1. La clessidra
Avendo 2 clessidre da tempi diversi, ad esempio da 5 e da 6 minuti, è possibile addizionare o sottrarre i tempi.

• Per addizionare i tempi, si fa partire una clessidra quando l'altra ha terminato.
  Per ottenere 17 minuti si esegue la seguente addizione di tempi:
  6 + 5+ 6
• Per sottrarre i tempi si fanno partire due clessidre assieme. Quando la più breve ha terminato, nell'altra rimane la differenza dei tempi.
  Per ottenere un minuto, si fanno partire assieme le due clessidre. Quando quella da 5 minuti ha terminato, in quella da 6 minuti rimane ancora 1 minuto il quale può essere misurato a partire da quell'istante.
• Una clessidra può anche essere fermata, disponendola orizzontalmente.

In tutte queste considerazioni si suppone che le clessidre vengano capovolte in un tempo nullo o trascurabile.

2. Le due clessidre
Si eseguono le seguenti operazioni con le clessidre.
11 - 7 = 4
4 + 11 = 5

In pratica si procede così:

• si fanno partire assieme la clessidra da 11 min e quella da 7 min;
• quando la clessidra da 7 min ha terminato, si ferma la clessidra da 11;
• osserviamo che la sabbia nella clessidra da 11 min è divisa in due parti che corrispondono a 11- 7 = 4 min e 7 min.
• a questo punto si può partire con la misura dei 15 min;
• prima si fanno scorrere i 4 min nella clessidra da 11 min;
• poi si capovolge la stessa clessidra e si fanno scorrere 11 min;
• 11 + 4 = 15 min.

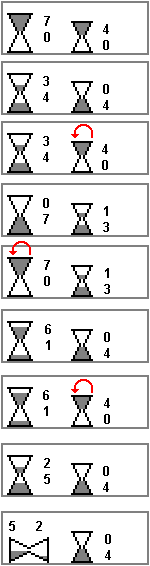
3. La cottura delle uova sode
Prima di cuocere le uova, Andrea Pinzimonio prepara le clessidre in modo da avere:

• la clessidra da 4 min pronta a partire;
• la clessidra da 7 min ferma su 5 + 2 min.

Dopodichè, in qualunque momento, si può eseguire l'addizione 5 + 4 = 9.

La seguente figura illustra la preparazione delle clessidre.

4. I cubetti di ghiaccio
Risposta inviata da Enrico De Vita, Giuseppe Pace e Massimiliano
Noi siamo riusciti a ghiacciare le 7 forme per cubetti di ghiaccio nel doppio del tempo necessario affinchè una forma si ghiacci.
Non pensiamo che si possa fare di meglio.
1° Metodo
Ghiacciare completamente una forma.
Inserire 2 cubetti di ghiaccio per ogni forma( 6 forme * 2 ghiacci = 12 cubetti) in questo modo:

Vaschetta vista dall'alto.
A = acqua - G = ghiaccio

Riempire di acqua le "vaschettine" vuote e poggiare le forme una sull'altra (i cubetti di ghiaccio sosterranno le vaschette).
L'ultima forma(priva di ghiaccio) si può poggiare in alto.

2° Metodo (con l'aiuto di Massimiliano)
Riempire di acqua 4 forme.
Alternare una forma piena d'acqua con una forma vuota capovolta.
Attendere che si formi il ghiaccio.
Ripetere l'operazione con le tre forme vuote.

Vincenzo Lombardo migliora il record di velocità.
Vorrei premettere che a mio parere il quesito sui cubetti di ghiaccio, per come è stato formulato, è più un problema di fisica che di pura logica; infatti già la domanda a cui si chiede di rispondere, qual è il tempo minimo per creare dei cubetti di ghiaccio, dovrebbe dipendere dal numero di operazioni che si compiono sulle vaschette, sulla velocità con cui vengono compiute etc.. Ammettiamo tuttavia che si intendesse chiedere qual è il tempo minimo di permanenza nel freezer delle vaschette affinchè si producano i cubetti.
Le soluzioni proposte sinora seguivano questa linea e il tempo minimo dimostrato era di due volte il tempo necessario a riempire una forma.

Voglio tuttavia proporvi una soluzione che migliora i tempi già ottenuti e che nel contempo vi mostri come il gioco resti soprattutto un problema di fisica.

Quello che interessa è poter creare il più rapidamente possibile un sostegno alle vaschette in modo che si possano sovrapporre senza compenetrarsi. Per far questo si possono  riempire 4 vaschette a metà (come in figura)

*Sezione trasversale di una vaschetta.

e le altre 3 sovrapporle in modo capovolto, alternate a quelle mezze piene. Sarà allora necessario attendere meno tempo rispetto a T (T= tempo necessario per ghiacciare una forma ) per ghiacciare l'acqua così utilizzata (attenzione non è T/2).
Abbiamo così ottenuto 4 *12 metà. Con queste metà possiamo creare 24 cubetti da utilizzare come sostegno, nello stesso modo proposto in una soluzione già data da altri.
Si potrebbe provare a rifare il gioco riempiendo un solo terzo delle 4 vaschette e i cubetti che si potrebbero creare sarebbero 4 * 12 terzi cioè 16 oppure riempire con un quarto d'acqua le vaschette e ottenere 12 cubetti di sostegno.
E' chiaro a questo punto che volendo ragionare in termini di stabilità non le riempiremo con meno acqua. Il tempo necessario a raggiungere lo scopo utilizzando questo tipo di soluzione risulterà certamente inferiore a 2T pur tuttavia non essendo valutabile poiché dipende dalla forma delle celle, dal materiale di cui sono composte le vaschette, etc... un problema fisico dicevo.
* Il ragionamento è stato fatto ipotizzando la forma dei cubetti rettangolare, ma è chiaro che altre forme permetterebbero comunque di scendere sotto 2T.

5. Le bistecche in padella
La sequenza più breve di cottura è illustrata nella seguente tabella.
Si indicano con F1, F2, F3 le tre fette per un verso e con RF1, RF2, RF3 le tre fette per l'altro verso.

Il questo modo si ottiene F1 tiepida, F2 e F3 calde, in 15 minuti.

6. Tre lavori, due persone
La sequenza dei lavori è illustrata nella seguente tabella.

7. Quattro lavori, una persona
Prepara la torta e la mette in forno regolando il timer su 30' di cottura: 20'
Carica lavatrice: 5'
Stira e guarda la TV: 60'
Stende: 5'

8. I quattro soldati
Ricordiamo i tempi di attraversamento:

• Andrea impiega 1 minuto ad attraversare la passerella;
• Bernardo impiega 2 minuti;
• Carlo impiega 5 minuti;
• Diego impiega 10 minuti.

Ecco la sequenza dei passaggi:

9. L'orologio a cucù
Tra un cucù e l'altro passa 1 sec. 11 sec.
tra un cucù e l'altro passano 1,2 sec. 12 sec

10. Lancette che si sovrappongono
11 volte, ogni ora + n/11 di ora.

11. Lancette perpendicolari
44 volte. Due volte ogni ora meno 1 volta tra le 2 e le 4 e una volta tra le 8 e le 10, sia A.M. che P.M.
(da verificare!?)

12. Orologi mal tarati
Consideriamo due orologi, A e B.
Entrambi segnano le ore 6 in punto ma l'orologio A ha le lancette installate correttamente mentre l'orologio B ha la lancetta dei minuti inserita nel perno delle ore e quella delle ore inserita nel perno dei minuti.
Le lancette sono indicate con a1, a2, b1, b2

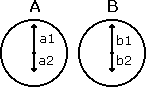
Di conseguenza, si ha che:

• a1 ruota 12 volte più velocemente di b1
  Chiediamoci: quando a1 e b1 occuperanno nuovamente la stessa posizione?
  La risposta è: dopo 1 giro + 1/11 di giro.

• b2 ruota 12 volte più velocemente di a2
  Chiediamoci: quando a2 e b2 occuperanno nuovamente la stessa posizione?
  La risposta è: dopo 1 giro + 1/11 di giro.

Perciò, dopo 1h +1/11 di h le lancette dei due orologi occuperanno nuovamente posizioni identiche.

Saranno le ore 7h 5min 27sec, ...

13. L'orologio di Immanuel Kant
dal testo del problema si può dedurre che la velocità a piedi di Kant è una costante universale.
Per cui:

• prima di uscire Kant diede la corda al proprio orologio e annotò l'ora, chiamiamola "ora x";
• appena giunto a casa del suo amico, Kant notò l'ora, indichiamola con a;
• quando uscì da casa del suo amico, Kant notò nuovamente l'ora, indichiamola con b;
• quando arrivò a casa propria, Kant annotò nuovamente l'ora che segnava il suo orologio, chiamiamola y.

A questo punto Kant calcolò:

Tempo lordo passato dal suo amico, compresi i viaggi di andata e ritorno:
TL = y - x

Tempo netto passato a casa del suo amico:
TN = b - a

Tempo del viaggio di ritorno:
TV = (TL - TN)/2

Ora esatta:
OE = b + TV

Naturalmente, Kant dovette aggiungere anche tutto il tempo impiegato per eseguire i calcoli descritti.

Fatto ciò tirò fuori l'orologio da tasca che gli aveva prestato l'amico e constatò con soddisfazione che la propria velocità a piedi era una costante universale!

14. L'orologiaio ubriaco

15. Gemelli che nacquero in mesi diversi
Uno nacque l'ultimo giorno di un mese, poco prima della mezzanotte.
L'altro nacque il primo giorno del mese successivo, poco dopo la mezzanotte.

16. Gemelli che vissero in secoli diversi
Il primo fu partorito, il 31 dicembre 1899 alle ore 23.45 e purtroppo morì prima della mezzanotte.
L'altro fu partorito il 1 gennaio 1900 alle ore 0.05 e visse meno di 100 anni.

17. Il compleanno dei gemelli
Aldo nacque il 28 febbraio di un anno non bisestile, poco prima della mezzanotte.
Baldo nacque il 1 marzo, poco dopo la mezzanotte.
Negli anni bisestili i loro compleanni cadono a distanza di 2 giorni.

18. Compleanno di gemelli a 10 giorni di distanza
Complimenti ad Alan Viezzoli
Nel 1582 Papa Gregorio XIII ha deciso di eliminare 10 giorni: dal 5 al 14 ottobre. Aldo è dunque nato alle 23:50 del 4/10/1582, Baldo alle 0:10 del giorno dopo, il 15/10/1582. Per questo motivo, dopo 50 anni (nel 1632, appunto) i loro compleanni distano dieci giorni.

19. Quanti anni ha Pippo
L'altro ieri: 30/12/1999, Pippo aveva 33 anni.
Ieri: 31/12/1999 ha compiuto 34 anni
Oggi: 1/1/2000 è nell'anno dei 35
L'anno prossimo, 31/12/2001, compirà 36 anni

20. Il compleanno di Pippo
43²=1849
44²=1936
45²=2025
Pippo aveva 44 anni nel 1936. Questa è l'unica soluzione umanamente plausibile.
Perciò nel 2000 egli compie 2000 - 1936 + 44 = 108 anni.

21. Strani compleanni
Perché si verifichi quella coincidenza, la persona deve essere nata in un anno le cui ultime due cifre formino un numero multiplo di 9.
Es: 1909, 1918, 1927, 1936, ...

22. Quanti anni ha Lucia?
Indichiamo con l l'età di Lucia e con m l'età di Monica.
Il seguente sistema risolve il problema:

l = 3m
l + 3 = 2(m + 3)

da cui si ottiene:

l = 9
m = 3

23. Orologio digitale
Otto volte.
0:00, 1:11, 2:22, 3:33, 4:44, 5:55, 11:11, 22:22

24. Trionfi dell' Inter
(Pasquale, 20/06/04 21:49)
Già: siamo alle ore 19 del 28/07/3456
Insomma, noi questa cosa non la vedremo.

25. Quando avrai la mia età
Riformulo il problema più dettagliatamente:
Io (oggi) ho il doppio dell'età che tu avevi quando io avevo la tua età (di oggi). Sapendo che quando tu avrai la mia età (di oggi), insieme avremo 90 anni, quanti anni abbiamo?

La risposta è:
tu oggi hai 30 anni e io 40.
Infatti quando io ne avevo 30 tu ne avevi 20 e quando ne avrai 40 io ne avrò 50.

Provo a dare una soluzione algebrica.

Considero la frase:
Io (oggi) ho il doppio dell'età che tu avevi quando io avevo la tua età (di oggi).

Supponiamo che tu oggi abbia X anni e che N anni fa io avessi X anni.
Posso scrivere:
1) N anni fa tu avevi X-N anni
2) oggi io ho X+N anni
Per la frase considerata X+N è il doppio di X-N, dunque:
X+N = 2(X-N)

Risolvendo questa equazione si ottiene:
X=3N

Quindi posso scrivere che:
3) oggi tu hai X=3N anni
4) oggi io ho X+N=4N anni

Considero la seconda frase:
Sapendo che quando tu avrai la mia età (di oggi), insieme avremo 90 anni

Mi chiedo: fra quanti anni avrai la mia età di oggi?
Visto che tu hai 3N anni e io ne ho 4N, tu avrai la mia età di oggi fra N anni.

Quindi posso scrivere che fra N anni:
5) tu avrai 4N anni
6) io avrò 5N anni

Ma siccome insieme avremo 90 anni, posso scrivere:
4N+5N=9N=90 anni
N=10 anni

In conclusione:
tu oggi=3N=30 anni
io oggi=4N=40 anni

Riporto anche la soluzione inviata da Giovanni Macchia.
Carissimi, innanzitutto contento di avervi ritrovato dopo tanto tempo. Io non ho la palpebra pesante data l'ora, ma sono reduce da una brutta influenza che mi ha tenuto a letto e pertanto un po' così e così lo sono. Comunque credo di avere trovato una soluzione semplice (anche se lunga a spiegare a parole). Si ottiene suddividendo il problema in due "scioglilingua".
Chiamerò 1° scioglilingua la frase "Io ho il doppio dell'età che tu avevi quando io avevo la tua età." e 2° scioglilingua la frase "Sapendo che quando tu avrai la mia età, insieme avremo 90 anni, quanti anni abbiamo?"

Indichiamo con x e y le età, con x > y. Premettiamo che la differenza di età tra i due è ovviamente data da x-y

"L'età che tu avevi quando avevo la tua età" è pertanto data da

y - (x-y)

e quindi, in base al primo scioglilingua si ottiene

x=2(y-(x-y))

che porta ad avere

a) 3x = 4y

Il secondo scioglilingua invece ci porta a dire che

y + (x-y) + x + (x-y) = 90

da cui si ottiene

3x-y=90

e, sostituendo la a) si ottiene

y=30, x = 40

A me sembra semplice ed elegante. A voi?

26. L'orologio stregato
Pasquale
Penso che dipenda dal tipo di suddivisione del quadrante e dall'approssimazione voluta. Se si suddivide il quadrante in 60 tacche da 1 minuto, intendendo che l'occhio non apprezza altro, allora la coincidenza avviene dopo 12 ore, alle 18,00.

Ronfo
L'ora di Pasquale è giusta ma ce ne sono anche altre prima.
L'orologio stregato segnerà nuovamente l'ora esatta alle 7, 5 minuti 27 secondi e (per i più pignoli) 3/11 di secondo.
Suggerimento :
per risolvere il problema fate finta che l'orologio abbia 4 lancette , un paio che si muovono regolarmente e l'altro paio scambiate...
Divertitevi

Paolo P.
Dopo 1h 05' dall' avvio dell' orologio:
l'ora effettiva è 7 05' 00''
la lancetta lunga segna la 1 00' 25''
la lancetta corta segna le 7 00' 00''

Trascorso un tempo t dalle 7 05 00 si ha :
ora effettiva 7 05 00 + t
lancetta lunga segna 1 00' 25'' + t/12 ossia, in minuti, 05' 25'' + t/12

perchè al tempo t la lancetta lunga segni il minutaggio esatto, occorre quindi che sia:
05'+ 25'' + t/12 = 05'+ 00'' + t
da cui si ricava t = 300 /11 [sec]= 27+3/11''

L'ora in cui la lancetta dei minuti segna il minutaggio esatto è quindi le 7 05 27+3/11''

Forse resta il dubbio se alle 7 05 27+3/11'' anche la lancetta corta si trovi in una posizione che corrisponda esattamente all'ora effettiva, ma questo avviene necessariamente, dato che dopo un tempo t dalle 7 05 00, la lancetta corta si trova alle 7 05 00 + t, per cui alle 7 05 27+3/11'' la lancetta corta si trova proprio alle 7 05 27+3/11''

Sito Web realizzato da Gianfranco Bo