Aritmetica Russa

Problemi fantastici tratti dalle Olimpiadi Matematiche Sovietiche
I seguenti problemi sono tratti dalle competizioni matematiche Russe del periodo 1961-1986.
I partecipanti sono ragazzi di 14 anni che frequentano l'8° anno di scuola.

Ordine delle cifre e divisibilità
Il numero naturale k ha la seguente proprietà: "Se n è divisibile per k allora il numero ottenuto da n invertendo l'ordine delle sue cifre è ancora divisibile per k".
Dimostrare che k è un divisore di 99.
(1° Tblisi 1967)

Sostituire le coppie
Molti "zero", "uno" e "due" sono scritti sulla lavagna.
Un anonimo cancella diverse coppie di numeri scrivendo al loro posto il numero diverso da entrambi i numeri cancellati. (ad es. 0, al posto della coppia {1,2}; 1 al posto di {0,2}; 2 al posto di {0,1}).
Dimostrare che se alla fine rimane un solo numero, questo non dipende dall'ordine con cui sono state cancellate le coppie
(Saratov, 1975)

Righe di 1000 numeri
Una riga di 1000 numeri è scritta alla lavagna.
Scriviamo una seconda riga di numeri sotto la prima, secondo la seguente regola: sotto ogni numero x scriviamo il numero naturale che indica quante volte x si trova nella prima linea.
Poi scriviamo una terza riga di numeri sotto la seconda, seguendo la stessa regola: sotto ogni numero y scriviamo il numero naturale che indica quante volte y si trova nella seconda linea.
E così via.
a) Dimostrare che c'è una riga uguale alla precedente.
b) Dimostrare che l'undicesima riga coincide con la dodicesima
c) Fornire un esempio di prima riga tale che la decima riga sia differente dalla undicesima riga.
(Dushanbe, 1976)

Sette elfi dividono il latte
Sette elfi siedono intorno ad una tavola rotonda.Ciascuno di essi ha una coppa.
Alcune coppe contengono del latte.
Ciascun elfo, a turno e in senso orario divide tutto il suo latte in parti uguali fra le altre sei coppe.
Dopo che il settimo elfo ha compiuto questa operazione, tutte le coppe contengono nuovamente la stessa quantità di latte che contenevano all'inizio.
Quanto latte contiene ciascuna coppa, se ci sono in tutto tre litri di latte?
(Tallinn, 1977)

Numeri buoni
Chiamiamo "buono" un numero di 2n cifre se è un quadrato perfetto e i numeri formati dalle sue prime n cifre e dalle sue ultime n cifre sono anche quadrati perfetti.
a) Trovare tutti i numeri "buoni" di 2 e di 4 cifre.
b) Esiste un numero "buono" di 6 cifre?
c) Dimostrare che esiste un numero "buono" di 20 cifre.
d) Dimostrare che esistono almeno 10 numeri "buoni" di 100 cifre.
e) Dimostrare che esistono numeri "buoni" di 30 cifre.
Prove that there exists 30-digit fine number.
(Tallinn, 1977)

Funzioni di funzioni
Sia f(x) = x² + x + 1.
Dimostrare che per ogni numero naturale m>1 i numeri m, f(m), f(f(m)), ... sono primi fra loro.
(Tashkent, 1978)

Tre automi giocano a carte
Ci sono 3 automi che elaborano carte contenenti coppie di numeri.
Il primo automa ricevendo la carta (a,b) produce la carta (a+1, b+1).
Il secondo automa ricevendo la carta (a,b) produce la carta (a/2, b/2) se a, b sono numeri pari e nulla in caso contrario.
Il terzo automa ricevendo la coppia di carte (a,b), (c,d) produce la carta (a,c).
Tutti gli automi, oltre alla carta prodotta, restituiscono anche la carta ricevuta.
Supponiamo di avere la carta (5,19) inizialmente.
E' possibile ottenere:
a) (1,50)?
b) (1,100)?
c) Supponiamo di avere inizialmente la carta (a,b) con a<b. Vogliamo ottenere la carta (1,n). Per quali n ciò è possibile?
(Tashkent, 1978)

Passaggio obbligato
Il professore scrive alla lavagna: "x² + 10x + 20"
Poi tutti gli alunni della classe, a turno, vanno alla lavagna e diminuisco o aumentano di 1 il termine noto o il coefficiente della x, ma non entrambi.
Alla fine ottengono: "x² + 20x + 10".
E' vero che ad un certo punto, durante le operazioni, alla lavagna è stata scritta un'equazione con le radici intere?
(Ashkhabad, 1984)

Sentinelle e pianeti
C'è esattamente un astronomo su ogni pianeta di un certo sistema. Egli osserva il pianeta più vicino. Il numero di pianeti è dispari e le distanze fra i pianeti sono tutte diverse fra loro.
Dimostrare che un pianeta di quel sistema non è osservato.
(Voronezh, 1966)

Potenza di 2
Tutti i numeri di 5 cifre, da 11111 a 99999 sono scritti su delle carte.
Queste carte sono allineate in un ordine arbitrario.
Dimostrare che il numero risultante, formato da 444445 cifre, non è una potenza di 2
(Simferopol, 1970)

Dalla versione inglese di Vladimir A. Pertsel

Given natural number k with a property "if n is divisible by k, than the number, obtained from n by reversing the order of its digits is also divisible by k".
Prove that the k is a divisor of 99.
(1° Tblisi 1967)

Several zeros, ones and twos are written on the blackboard. An anonymous clean in turn pairs of different numbers, writing, instead of cleaned, the number not equal to each. (0 instead of pair {1,2}; 1 instead of {0,2}; 2 instead of {0,1}).
Prove that if there remains one number only, it does not depend on the processing order.
(Saratov, 1975)

A row of 1000 numbers is written on the blackboard. We write a new row, below the first according to the rule: We write under every number a the natural number, indicating how many times the number a is encountered in the first line. Then we write down the third line: under every number b -- the natural number, indicating how many times the number b is encountered in the second line, and so on.
a)
Prove that there is a line that coincides with the preceding one.
b)
Prove that the eleventh line coincides with the twelfth.
c)
Give an example of the initial line such, that the tenth row differs from the eleventh.
(Dushanbe, 1976)

Seven elves are sitting at a round table. Each elf has a cup. Some cups are filled with some milk. Each elf in turn and clockwise divides all his milk between six other cups. After the seventh has done this, every cup was containing the initial amount of milk.
How much milk did every cup contain, if there was three litres of milk total?
(Tallinn, 1977)

Let us call "fine" the 2n-digit number if it is exact square itself and the two numbers represented by its first n digits (first digit may not be zero) and last n digits (first digit may be zero, but it may not be zero itself) are exact squares also.
a)
Find all two- and four-digit fine numbers.
b)
Is there any six-digit fine number?
c)
Prove that there exists 20-digit fine number.
d)
Prove that there exist at least ten 100-digit fine numbers.
e)
Prove that there exists 30-digit fine number.
(Tallinn, 1977)

Let f(x) = x² + x + 1.
Prove that for every natural m>1 the numbers m, f(m), f(f(m)), ... are relatively prime.
(Tashkent, 1978)

Given three automates that deal with the cards with the pairs of natural numbers. The first, having got the card with (a,b), produces new card with (a+1,b+1); the second, having got the card with (a,b), produces new card with (a/2,b/2), if both a and b are even and nothing in the opposite case; the third, having got the pair of cards with (a,b) and (b,c) produces new card with (a,c). All the automates return the initial cards also. Suppose there was (5,19) card initially. Is it possible to obtain
a)
(1,50)?
b)
(1,100)?
c)
Suppose there was (a,b) card initially (a<b). We want to obtain (1,n) card. For what n is it possible?
(Tashkent, 1978)

The teacher wrote on a blackboard: " x² + 10x + 20 " Then all the pupils in the class came up in turn and either decreased or increased by 1 either the free coefficient or the coefficient at x, but not both. Finally they have obtained: " x² + 20x + 10 ".
Is it true that some time during the process there was written the square polynomial with the integer roots?
(Ashkhabad, 1984)

There is exactly one astronomer on every planet of a certain system. He watches the closest planet. The number of the planets is odd and all of the distances are different.
Prove that there one planet being not watched.
(Voronezh, 1966)

All the 5-digit numbers from 11111 to 99999 are written on the cards. Those cards lies in a line in an arbitrary order.
Prove that the resulting 444445-digit number is not a power of two.
(Simferopol, 1970)

Risposte & riflessioni

Righe di 1000 numeri
Una riga di 1000 numeri è scritta alla lavagna.
Scriviamo una seconda riga di numeri sotto la prima, secondo la seguente regola: sotto ogni numero x scriviamo il numero naturale che indica quante volte x si trova nella prima linea.
Poi scriviamo una terza riga di numeri sotto la seconda, seguendo lastessa regola: sotto ogni numero y scriviamo il numero naturale che indica quante volte y si trova nella seconda linea.
E così via.
a) Dimostrare che c'è una riga uguale alla precedente.
b) Dimostrare che l'undicesima riga coincide con la dodicesima
c) Fornire un esempio di prima riga tale che la decima riga sia differente dalla undicesima riga.
(Dushanbe, 1976)

Ringrazio Sprmnt21 per la soluzione
Spero che sia chiaro (nonostante i problemi di formattazione).

Indico con A,B, ..., F sia gli elfi che le quantita' di latte dei sette elfi all'inizio (e alla fine) del "gioco". Nelle righe indicate con 1,2, ..., 7 metto le quantita' di latte contenute nelle coppe dopo il corrispondente "giro". Dopo ogni "giro" l'elfo che distribuisce rimane a secco. Da questo deriva, in particolare, che l'elfo G alla fine e quindi all'inizio non ha latte nella sua coppa.

...A...B....C....D....E....F....G..
+----+----+----+----+----+----+----+
1|.0..|....|....|....|....|....|....|
|....|....|....|....|....|....|....|
+----+----+----+----+----+----+----+
2|....|.0..|....|....|....|....|....|
|....|....|....|....|....|....|....|
+----+----+----+----+----+----+----+
3|....|....|.0..|....|....|....|....|
|....|....|....|....|....|....|....|
+----+----+----+----+----+----+----+
4|....|....|....|.0..|....|....|....|
|....|....|....|....|....|....|....|
+----+----+----+----+----+----+----+
5|....|....|....|....|.0..|....|....|
|....|....|....|....|....|....|....|
+----+----+----+----+----+----+----+
6|....|....|....|....|....|.0..|....|
|....|....|....|....|....|....|....|
+----+----+----+----+----+----+----+
7|....|....|....|....|....|....|.0..|
|....|....|....|....|....|....|....|
+----+----+----+----+----+----+----+

Dopo il settimo passaggio, le quantita sono quelle riportate nella riga 7. Come si nota F e' passato da 0 ad F. Questo vuol dire che F e' 1/6 di quanto aveva G prima del 7° giro, cioe (6,G)=6F. Di fatto ogni elfo da A ad F al settimo giro ha ricevuto una quantita' di latte pari ad F. Pertanto si puo' riempire la sesta riga come riportato nella seguente tabella. Con analogo ragionamento si ha che (5,F)=6(E-F) da cui si ricavano gli altri valori della 5 riga e cosi via ottenendo il quadro riportato sotto.

...A......B......C......D......E......F......G...
+------+------+------+------+------+------+------+
|......|......|......|......|......|......|......|
1|..0...|6(A-B)|......|......|......|......|......|
|......|......|......|......|......|......|......|
+------+------+------+------+------+------+------+
|......|......|......|......|......|......|......|
2|.A-B..|..0...|6(B-C)|......|......|......|......|
|......|......|......|......|......|......|......|
+------+------+------+------+------+------+------+
|......|......|......|......|......|......|......|
3|.A-C..|.B-C..|..0...|6(C-D)|......|......|......|
|......|......|......|......|......|......|......|
+------+------+------+------+------+------+------+
|......|......|......|......|......|......|......|
4|.A-D..|.B-D..|.C-D..|..0...|6(D-E)|......|......|
|......|......|......|......|......|......|......|
+------+------+------+------+------+------+------+
|......|......|......|......|......|......|......|
5|.A-E..|.B-E..|.C-E..|.D-E..|..0...|6(E-F)|......|
|......|......|......|......|......|......|......|
+------+------+------+------+------+------+------+
|......|......|......|......|......|......|......|
6|.A-F..|.B-F..|.C-F..|.D-F..|.E-F..|..0...|..6F..|
|......|......|......|......|......|......|......|
+------+------+------+------+------+------+------+
|......|......|......|......|......|......|......|
7|..A...|..B...|..C...|..D...|..E...|..F...|..0...|
|......|......|......|......|......|......|......|
+------+------+------+------+------+------+------+

Si noti che il valore di F dopo, ad esempio, il V passaggio cioe' la casella (5,F) e' dato da

6(E-F)= F+A/6+(A-B)+(B-C)+(C-D)+(D-E)=F+A/6+(A-E).

Analogamente per le caselle della stessa diagonale (4,E), (3,D), (2,C) ed (1,B) si ha:

6(D-E)= E+A/6+(A-B)+(B-C)+(C-D)=E+A/6+(A-D);

6(C-D)= E+A/6+(A-B)+(B-C)= D+A/6+(A-C);

6(B-C)= C+A/6+(A-B)

6(A-B)= B+A/6

Risolvendo a ritroso, si ha che B=5/6A; C=2/3A; D=1/2A; E=1/3A; F=1/6A.

Da cui conoscendo la somma A+B+C+D+E+F+G=s si ricavano i singoli valori

Funzioni di funzioni
Sia f(x) = x² + x + 1.
Dimostrare che per ogni numero naturale m>1 i numeri m, f(m), f(f(m)), ... sono primi fra loro.
(Tashkent, 1978)

Passaggio obbligato
Il professore scrive alla lavagna: " x² + 10x + 20 "
Poi tutti gli alunni della classe, a turno, vanno alla lavagna e diminuisco o aumentano di 1 il termine noto o il coefficiente della x, ma non entrambi.
Alla fine ottengono: " x² + 20x + 10 ".
E' vero che ad un certo punto, durante le operazioni, alla lavagna è stata scritta un'equazione con le radici intere?
(Ashkhabad, 1984)

Ringrazio Francesco Veneziano per la risposta
Che problema simpatico!
Se x^2+bx+c=0 è la nostra equazione, consideriamo la quantità c-b+1; all'inizio vale 9, alla fine vale -9. Poiché ad ogni mossa questa quantità può variare solo di 1 deve esserci un momento in cui essa vale 0; dimostriamo che in quel momento l'equazione ha radici intere.
Se x^2+Bx+C=0 e B=C+1 abbiamo che x^2+(C+1)x+C=0 e (x+1)(x+C)=0, e quindi le due soluzioni -1 e -C sono intere.

Ringrazio Sprmnt21 per la soluzione
Provo a dare una soluzione "geometrica" al problema. Come osservato in precedenza la situazione data e' equivalente a chiedersi se un qualsiasi percorso da P(10,20) ad A(20,10) a passi di lunghezza uno nelle quattro direzioni N-S-E-O passa da un punto tale che il polinomio di II° associato abbia zeri interi.

Dato x^2+a*x+b=(x-x1)(x-x2) si ha che -a=x1+x2 e b=x1*x2.

Si nota facilmente che la coppia (a,b)=(c, c-1) e' una coppia a cui, per ogni c, corrispondo x1 ed x2 interi precisamente x1=1 ed x2=c-1 (o viceversa).
Ma tutta la punteggiata (c, c-1) sta su una retta parallela alla bisettrice del primo quadrante e "distante" un solo passo da questa. Pertanto, siccome P ed A stanno da parti opposte rispetto ad essa, e' necessario che un QUALSIASI percorso da P ad A la tocchi.

Trenta tazze di latte
Ci sono 30 tazze uguali, ciascuna contenete del latte.
Un elfo tenta di fare in modo che tutte le tazze contengano la stessa quantità di latte.
Prende due tazze e porta il latte allo stesso livello in entrambe.
Può esistere una distribuzione iniziale del latte tale che l'elfo non riesca a raggiungere il suo scopo in un numero finito di passi?
(Ulyanovsk, 1986)

Ringrazio Alessandro Torelli per la soluzione
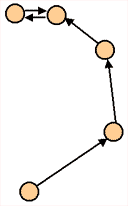
Possiamo rappresentare il problema con un grafo orientato e pesato G, in cui i nodi sono i pianeti, e c'è un arco U->V di peso d se U osserva V e d è la loro distanza.

Supponiamo per assurdo che esista una configurazione C t.c. tutti i pianeti sono osservati.
Possiamo rappresentare C con il grafo G che deve avere le seguenti proprietà:

1) Da ogni nodo esce uno ed un solo arco (c'è solo un astronomo su ogni pianeta).

2) In ogni nodo entra uno ed un solo arco (Se X fosse osservato da due astronomi distinti rimarrebbero n-1 pianeti e n-2 astronomi e non potrei osservarli tutti).

Sia ora d la minima tra tutte le distanze (d è unica perchè per ipotesi le distanze sono tutte distinte), e siano X,Y i due pianeti t.c. Distanza(X,Y) = d.
Banalmente X osserva Y e Y osserva X, quindi in G avremo un arco X->Y e uno Y->X.
Per le proprietà 1) e 2) X e Y non hanno altri archi entranti/uscenti, quindi posso eliminarli dal grafo e considerare il problema equivalente con n-2 nodi sul
sottografo G' = G - ({X},{Y}).
Iterando il ragionamento su G' posso togliere ad ogni passo due nodi alla volta fino a rimanere con un solo nodo Z (n è dispari).
Dato che Z deve osservare un pianeta e non può osservare se stesso, sarà costretto ad osservare il più vicino tra i pianeti che ho eliminato dal grafo in uno dei passi precedenti (ossia un pianeta già osservato), quindi in G esiste almeno un nodo che è osservato da due pianeti distinti, per cui C non può essere valida.