
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Una sequenza scoperta da Lothar Collatz
e diffusa da Helmut Hasse, Stanislaw Ulam, S. Kakutani
Questa pagina contiene codice javascript
può essere scaricata ed eseguita senza essere collegati ad internet
Grazie a Peppe per averci ricordato questo problema.
Il problema era già stato proposto da Gianvittorio Righi nelle Ricreazioni
ricevute di Marzo 2001 (41. Ma perché sempre 1?)
La congettura di Collatz ovvero il problema 3x+1 Scegli un numero intero x e applica la seguente operazione, che si chiama funzione C:
Il risultato è un nuovo numero, C(x). Ripeti l’operazione sul nuovo numero, ottenendo C(C(x)) e così via. Qualunque sia il numero x di partenza, continuando a ripetere l’operazione, arriverai sempre a ottenere il numero 1 dopo un numero finito di passi. Se continui, finirai intrappolato in un ciclo senza fine: 4, 2, 1, 4, 2, 1, ... |
Per esempio: partiamo da 7.
E' dispari, quindi faccio 3·7+1=22.
Pari, 22:2=11.
Dispari, 11·3+1=34.
Pari, 34:2=17.
Dispari, 17·3+1=52.
Pari, 26.
Pari, 13.
Dispari, 40.
Pari, 20.
Pari, 10.
Pari, 5.
Dispari, 16.
Pari, 8.
Pari, 4.
Pari, 2.
Pari, 1.
Da questo punto in poi si entra in un ciclo infinito: 4,2,1,4,2,1,4,2,1.....
L'algoritmo di Collatz in javascript
Codice javascript di Gianfranco Bo
La congettura di Collatz-Hasse-Ulam-Kakutani
Applicando l'operazione di Collatz a qualunque numero intero positivo, si
finisce per ottenere sempre 1 (dopo un numero finito di cicli).
---
Aggiornamento del 2019
Il mitico Terence Tao ha dimostrato nel settembre 2019 che:
"ALMOST ALL ORBITS OF THE COLLATZ MAP ATTAIN ALMOST BOUNDED VALUES"
Si potrebbe tradurre così:
"Quasi tutte le traiettorie del grafo di Collatz raggiungono valori quasi limitati."
E' interessante capire cosa intendono i matematici quando parlano di "quasi tutti" gli elementi di un insieme infinito.
E anche cos'è una quasi-dimostrazione.
Per chi vuole approfondire, c'è l'articolo di Tao su ArXiv:
https://arxiv.org/abs/1909.03562
---
Aggiornamento del 2010
Il libro The Ultimate Challenge: The 3x+1 Problem, a cura di Jeffrey C. Lagarias, 2010, contiene alcuni articoli aggiornati al 2010.
Ma per me è stato davvero emozionante trovare i sei primi articoli sul problema e le relative domande, di L. Collatz, J. H. Conway, H. S. M. Coxeter, C. J. Everett e R. K. Guy, ciascuno con commenti editoriali.
Particolarmente illuminante l'articolo: On the motivation and origin of the (3x + 1) problem di Lothar Collatz.
Ecco come inizia l'articolo:

Questo è il grafo del problema 3x+1 disegnato da Collatz nell'articolo:
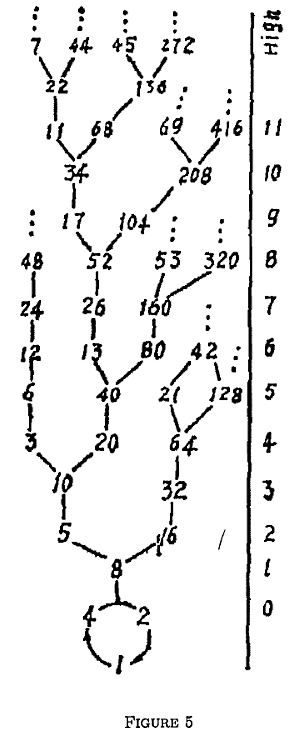
---
Nota storica. (devo rivederla in base al libro del 2010)
All'inizio degli anni '30 (1930), Lothar Collatz, uno studente dell'università di Hambourg, si occupava della teoria dei numeri e della teoria dei grafi. Partiva da un numero intero positivo, gli applicava un algoritmo iterativo, tracciava i grafi associati e si poneva delle domande... che sono ancora senza risposta.
Il matematico tedesco Helmut Hasse, amico di Collatz, diffuse il problema noto anche con il nome "algoritmo di Hasse" o "problema 3x+1".
Poiché Hasse presentò il problema negli anni '50 durante una visita all'università di Syracuse (vicino a New York), propose di battezzarlo "problema di Syracuse".
Il matematico polacco Stanislaw Ulam, fece circolare l'algorimo all'Università di Los Alamos, dove lavorava durante la seconda guerra mondiale. Per questo il problema è anche noto con il nome "problema di Ulam".
Negli anni '60 S. Kakutani si interessò nuovamente al problema e la congettura prese il nome di "problema di Kakutani".
Altre formulazioni del problema di Collatz
Il problema originale di Collatz
Sembra che fra le note di Collatz datate 1 luglio 1932 si trovi questo
problema:
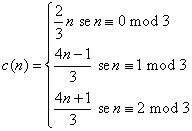
Il problema 3x+1
L'algoritmo si può esprimere come iterazione della seguente funzione.
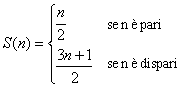
I risultati delle iterazioni si possono rappresentare con un grafo di questo tipo, chiamato grafo (o mappa) di Collatz della funzione S(n)

Giovanni Macchia (soluzione inviata nel Marzo 2001)
Il problema è il cosiddetto "problema 3x +1" . E' posto nel seguente
modo.
Definiamo la serie Si con elemento iniziale S0 = n, con n intero positivo
e
Si =
La serie si definisce convergente, se
(1) Min (n) = lim k->¥ Min(S0, S1, ..., Sk) = 1
Se si dimostra che Min(n) = 1 per ogni n naturale, allora si capisce perché ciclicamente si arriva a ottenere sempre il numero 1, come richiesto da Gianvittorio Righi.
Attualmente, non è stato dimostrato per tutti i casi. Esiste solo una dimostrazione debole (molto importante peraltro) dovuta a Terras, che afferma (introducendo il concetto di stopping time) che la maggioranza degli interi positivi ha il comportamento (1). Per chi volesse approfondire l'argomento suggerirei i seguenti siti (il secondo è per palati molto raffinati... )
http://personal.computrain.nl/eric/wondrous/#part1
http://www.cecm.sfu.ca/organics/papers/lagarias/paper/html/paper.html
---
Pace e bene a tutti!
Gianfranco Bo
Data creazione: 2003
Ultimo aggiornamento: gennaio 2020
Sito Web realizzato da Gianfranco Bo