[BASE Cinque - Appunti di Matematica ricreativa]
Il resto di una divisione può essere negativo? Ovvero, quanto fa a MOD b?
N.B. Ho completamente riscritto questa pagina perché era poco chiara.
Le seguenti riflessioni nascono da una domanda posta da Pietro Vitelli al Forum.
Salve gente, scusate la banalità, ma:
-14 mod 16
a che cosa è uguale? a -14 o a 2?
Sul blog di Umberto Cerruti ho trovato un calcolatore implementato in javascript, che permette di effettuare anche il modulo di un numero e mi da che è uguale a 2, mentre io pensavo fosse uguale a -14.
Questo è il link: http://alpha01.dm.unito.it/personalpages/cerruti/cp0/calc8.html
Come funziona l'aritmetica modulare per i negativi?
1. Nei numeri naturali (non c'é problema)
Se a, b sono numeri naturali, con b diverso da 0, allora esistono due numeri naturali (unici), q, r tali che:
a = qb + r
con 0 ≤ r < b
q si chiama quoziente e r resto della divisione di a per b.
L'algoritmo della divisione a/b dimostra l'esistenza e l'unicità di q, r e inoltre permette di trovarli.
Esempi
Dividendo 13 per 10, 1 è il quoziente e 3 è il resto, perché 13=1×10+3.
Dividendo 26 per 4, 6 è il quoziente e 2 è il resto, perché 26=6×4+2.
Dividendo 56 per 7, 8 è il quoziente e 0 è il resto, perché 56=7×8+0.
Nei numeri naturali si può dire che: a mod b è il resto della divisione di a per b
Esempio
26 mod 4 = 2
2. Nei numeri interi relativi
Entrando nei numeri relativi c'è un po' di confusione perché circolano
almeno due diverse definizioni autorevoli di divisione intera,
resto, e operatore mod.
Per questo motivo, diversi software possono dare diverse risposte, sebbene
riconducibili le une alle altre.
Premessa: le funzioni floor(x) e ceiling(x)
In informatica, ma anche in matematica si utilizzano due particolari
funzioni di "arrotondamento" dei numeri, chiamate floor
(pavimento) e ceiling (soffitto).
floor(x) approssima un numero reale x al più grande
intero <= x e si indica col simbolo: 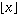
Esempi
floor(3.7) = 3
floor(-3.7) = -4
ceiling(x) approssima un numero reale x al più piccolo
intero >= x e si indica col simbolo: 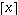
Esempi
ceiling(3.7) = 4
ceiling(-3.7) = -3
I matematici tendono ad accettare il seguente teorema e
le definizioni che ne seguono.
| Teorema (tratto da un testo di matematica) Siano a; b due interi, con b <> 0. Allora esistono due, e due soli, interi q; r, tali che: a = bq + r con 0 <= r < |b|. Definizioni Esempi: La divisione intera, quindi, può essere definita come: In questo caso si può dire che il resto è quel numero positivo che bisogna addizionare al prodotto del divisore per il quoziente per ottenere il dividendo. Così risultano definiti la divisione intera e il resto. Ma che ne
è del mod? Denotiamo inoltre con Secondo questa definizione, a mod b, coincide con il resto della
divisione di a per b ed è sempre positivo. |
Gli informatici, invece, tendono ad utilizzare definizioni leggermente diverse.
| Definizioni
Siano x reale, n, d interi e sia la funzione TRUNC così definita: TRUNC(x) = floor(x) se x>=0 (il più grande intero <= x) Esempi Indichiamo a/b la divisione fra numeri reali. Definizione di divisione intera a div b = TRUNC(a/b) Esempi Definizione di resto della divisione intera a rem b = a-b*TRUNC(a/b) Esempi Cioè il resto ha lo stesso segno del dividendo. Definizione dell'operatore mod a mod b = a - b * floor(a/b) Esempi Definizioni tratte da: |
Salvo errori & omissioni
Però sarebbe bello mettersi d'accordo!
Data creazione: febbraio 2006
Ultimo aggiornamento: marzo 2006
xhtml 1.1
Sito Web realizzato da Gianfranco Bo