[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Mandala Aritmetici

Un particolare ringraziamento a Gongolo per aver postato questo problema al Forum e a Francesco Veneziano e Alex per le risposte fornite.

1. Caramelle e aritmetica modulare
Durante l'intervallo, i bambini sono seduti in cerchio attorno alla maestra per fare un gioco.
La maestra sceglie un bambino e gli dà una caramella.
Poi, procedendo in senso anti-orario, salta 1 bambino e dà una caramella al successivo; quindi ne salta 2 e dà una caramella al successivo, poi ne salta 3 e così via.
Quanti devono essere i bambini affinché, dopo un numero finito di giri, tutti abbiano ricevuto almeno una caramella?

Questo problema è tratto dall'APMO (Asian Pacific Mathematical Olympiad) 1991.
Ho introdotto una piccola variante: il senso di distribuzione delle caramelle è anti-orario anziché orario.

Risposte & riflessioni

La prima risposta è quella di Alex.
Il numero dei bambini deve essere uguale a una potenza di 2,
inoltre, se la maestra vuole anche essere sicura che le caramelle rimangano distribuite in parti uguali tra i bambini, è sufficiente che disponga di un numero di caramelle uguale al numero dei bambini moltiplicato per un numero pari.

Ho trovato la soluzione al computer (variando il numero dei bambini da 2 a 20000), ma non ho dimostrato che valga anche se il numero dei bambini è maggiore di 20000.

Non sono stato capace di trovare la dimostrazione. Mi piacerebbe che qualcuno la trovasse, mi è rimasta la curiosità!

Gianfranco Bo
Supponiamo di avere n bambini disposti in fila e numerati 1, 2, 3, ..., n.

La maestra darà le caramelle ai bambini numero 1, 3, 6, 10, 15, ... (k(k+1)/2). E' la sequenza dei numeri triangolari.

Se invece i bambini sono disposti in cerchio, la k-esima caramella toccherà al bambino:

(k(k+1)/2) MOD n

Cercando di capire la struttura intima di questo gioco, ho scritto alcuni programmi per computer che visualizzano la distribuzione delle caramelle.

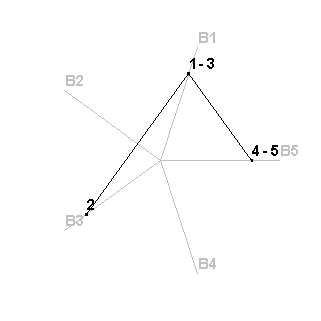
Ecco un esempio con 5 bambini:

Esempio con 5 bambini

le lettere grigie B1, B2, B3, ... indicano i bambini;
i bollini numerati in nero indicano l'ordine con cui vengono distribuite le prime 5 caramelle;
le linee nere indicano il percorso compiuto dalla maestra per consegnare le caramelle; in questo caso il percorso è B1-B3-B1-B5-B5.

Come si vede, i bambini B2 e B4 non ricevono caramelle mentre i bambini B1 e B5 ricevono 2 caramelle.

Dalla 6° caramella in poi il ciclo si ripete uguale. Come facciamo ad esserne sicuri?

Perché la 4° e la 5° caramella sono date allo stesso bambino in due turni successivi. Ciò significa che il "salto" che ha fatto la maestra è uguale ad un multiplo del numero dei bambini, nel nostro caso 5k. Il prossimo sarà il bambino 5k+1, poi 5k+3, poi 5k+6, e così via.

Ma, attenzione:

5k+1 MOD 5 = 1

5k+3 MOD 5 = 3

5k+6 MOD 5 = 1

etc.

Quindi, in questo caso, se un bambino non riceve una caramella nel primo ciclo allora non ne riceverà mai più. In quali altri casi accade ciò?

Consideriamo un esempio con 6 bambini.

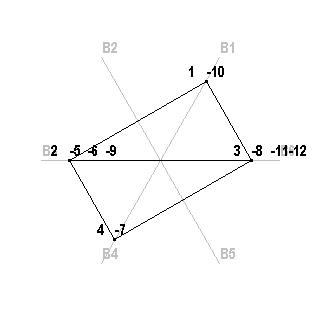
Esempio con 6 bambini

In questo esempio il ciclo si ripete dalla 12° caramella in poi e i bambini B2 e B5 non riceveranno mai caramelle.

Con le potenze di 2, invece, si ottengono delle figure più regolari. Il mandala comincia a spuntare all'orizzonte!

Esempio con 8 bambini
B8 riceve la prima caramella al 15° turno

Esempio con 16 bambini
B16 riceve la prima caramella al 31° turno

Nell'esempio con n=8 si nota che tutti i bambini tranne l'ultimo, B8, ricevono una caramella nel primo ciclo. B8 riceverà una caramella al 15° e al 16° turno. Negli esempi di fig. 3 e fig. 4, in cui n è una potenza di 2, tutti i bambini ricevono almeno una caramella

2. Alla ricerca del Mandala
Che cosa accadrebbe se i bambini fossero centinaia di migliaia?

Assegnando colori ciclici alle linee, si ottengono delle incredibili animazioni, il cui ultimo fotogramma è un pasticcio apparentemente caotico come quelli che vedete nelle figure qui sotto.

Le linee formano una poligonale che rappresenta il percorso compiuto dalla maestra per consegnare le caramelle ai bambini.

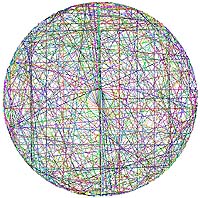
Immagine del percorso che dovrebbe fare la maestra se i bambini fossero 1.024.
Ciascuna linea è colorata con un colore diverso.

Tuttavia, se i bambini sono più di 2¹⁶, durante l'animazione, si notano come dei flash colorati, in cui lampeggiano per una frazione di secondo delle configurazioni regolari.

Per fissarle occorre fermare il programma nell'istante giusto.

Gli istanti giusti cadono in precise frazioni del percorso.

Qui di seguito vedete alcuni esempi.

I colori alle linee sono stati assegnati con la seguente regola: se il numero di colori diversi è n allora la linea i-esima è colorata con il colore i MOD n.

2¹⁶ bambini 2 colori, fermato a 1/2 del percorso.

2¹⁶ bambini 3 colori, fermato a 1/3 del percorso.

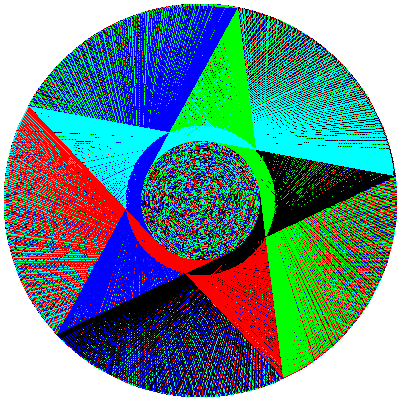
2²⁰ bambini 5 colori, fermato a 2/5 del percorso.

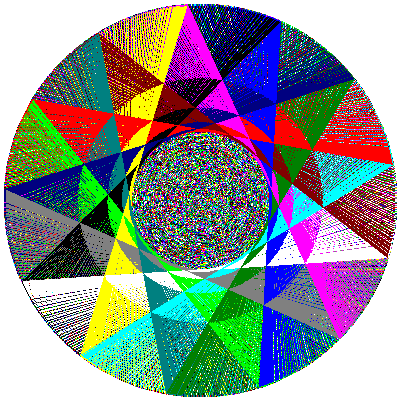
2²² bambini 13 colori, fermato a 8/13 del percorso.

Che cosa è il mandala.
Il mandala è un cerchio, una comunità, una connessione. Aiuta a meditare, concentra l'attenzione, protegge dalle distrazioni esterne e interne. E' un luogo in cui si entra per poi scoprire che è dentro di noi. E' la porta attraverso la quale possiamo stabilire un contatto con il nostro inconscio. Secondo lo psicologo Carl Gustav Jung, chiunque è prossimo a completare il processo di individuazione, cioè sta per conoscere veramente se stesso, incontra un mandala. Lo può incontrare in un sogno o in un disegno tracciato con le sue proprie mani. Chi è matematico, lo può vedere in un problema geometrico, ma anche in un problema aritmetico.

Il programma in DECIMAL BASIC che realizza i grafici visti sopra è il seguente.
Attenzione: bisogna intervenire su almeno 3 variabili.

Il numero dei bambini è dato dalla variabile q.

Se volete interrompere il programma ad una certa frazione del numero dei bambini, dovete intervenire sulle due variabili:

fraz, che indica il denominatore e anche il numero di colori utilizzati

ng che indica il numeratore

OPTION ANGLE DEGREES
LET q=2^20
LET fraz=5
LET ng= 3
LET q1 = 250
LET f=(q1/q)
LET cr=5
SET WINDOW -q1-cr,q1+cr,-q1-cr,q1+cr
LET xv=0
LET yv=0
LET ro=q/fraz*ng
LET th=0
LET xv=fraz/ng*f*ro*COS(th)
LET yv=0
FOR i = 1 TO q/fraz*ng
LET n=n+i
LET t=MOD(n,q)
IF t=0 THEN LET t=q
LET th=t*(360/(q) )
LET x=fraz/ng*f*ro*COS(th)
LET y=fraz/ng*f*ro*SIN(th)
SET LINE COLOR MOD(i , fraz)+1
PLOT LINES: xv,yv;x,y
LET xv=x
LET yv=y
NEXT i
END

3. Un altro punto di vista.
Se ora cambiamo il punto di vista, possiamo creare un altro tipo di grafici molto interessante.

4 bambini - 8 turni

In questo grafico i raggi grigi indicano i turni di distribuzione (T1, T2, ...).
Su ogni raggio sono presenti delle tacche grigie che indicano i bambini (B1, B2, ...).
I bollini quadrati neri indicano quale bambino riceve la caramella.
Le linee nere indicano l'ordine di distribuzione.

Vediamo cosa succede con alcune potenze di 2.

8 bambini - 16+1 turni

16 bambini - 32+1 turni

Si nota che le figure generate hanno un solo asse di simmetria e che tutti i bambini ricevono 2 caramelle in 2 cicli.

Vediamo ora cosa succede con alcuni numeri primi.

5 bambini - 10+1 turni

7 bambini - 14+1 turni

11 bambini - 22+1 turni

19 bambini - 38+1 turni

In questo caso, le figure generate hanno due assi di simmetria, e ciò è in relazione col fatto che alcuni bambini ricevono più di una caramella prima della conclusione del primo ciclo, mentre altri bambini rimangono senza caramelle.

Il programma in DECIMAL BASIC che realizza i grafici visti sopra è il seguente:

Il numero dei bambini è dato dalla variabile q. Cambiando il suo valore otterrete i grafici che vi interessano.

OPTION ANGLE DEGREES

LET q=16

LET q1 = 160

LET f=(q1/(q+1))

LET cr=30

SET WINDOW -q1-cr,q1+cr,-q1-cr,q1+cr

LET lt=1

FOR i = 1 TO 2*q

SET LINE COLOR 15

LET ro= (q+1)*f

LET th=i*(360/(2*q))

LET x=ro*COS(th)

LET y=ro*SIN(th)

PLOT LINES: 0,0;x,y

SET TEXT COLOR 15

PLOT TEXT,AT x,y:"T"&STR$(i)

FOR j = 1 TO q

LET ro= j*f

LET x=ro*COS(th)

LET y=ro*SIN(th)

SET AREA COLOR 15

PLOT AREA: x-lt,y-lt; x+lt,y-lt;x+lt,y+lt;x-lt,y+lt

NEXT j

NEXT i

LET ro= 1

LET th=(360/(2*q))

LET xv=f*ro*COS(th)

LET yv=f*ro*SIN(th)

FOR i = 1 TO 2*q+1

LET n=n+i

SET LINE COLOR 1

LET ro= MOD( n , q )

IF ro=0 THEN LET ro=q

LET th=i*(360/(2*q))

LET x=f*ro*COS(th)

LET y=f*ro*SIN(th)

SET LINE COLOR 1

PLOT LINES: xv,yv;x,y

SET AREA COLOR 1

PLOT AREA: x-lt,y-lt; x+lt,y-lt;x+lt,y+lt;x-lt,y+lt

SET TEXT COLOR 1

!'PLOT TEXT,AT x,y:"B"&STR$(ro)

LET xv=x

LET yv=y

NEXT i

END

4. Una piccola dimostrazione

Supponiamo di avere n bambini disposti in cerchio e numerati 1, 2, 3, ..., n.

Abbiamo visto all'inizio che la k-esima caramella tocca al bambino (k(k+1)/2) MOD n.

La soluzione del problema è: tutti i bambini ricevono almeno una caramella se e solo se il loro numero è una potenza di 2.

Qui di seguito vediamo soltanto la prima parte della dimostrazione.

Cominciamo col dimostrare che se n è una potenza di 2 allora (k(k+1)/2) MOD n assume tutti i valori da 1 a n-1 al variare di k da 1 a n-1 (non nello stesso ordine).

Facciamo un ragionamento per assurdo: supponiamo che esistano 2 interi positivi distinti, r, s (con r>s) entrambi minori o uguali a n-1 per cui si abbiano due resti uguali. Allora dovrebbe accadere che:

(r(r+1)/2) MOD n = (s(s+1)/2) MOD n

[(r(r+1)/2) - (s(s+1)/2)] MOD n = 0

(r² + r - s² - s)/2 MOD n = 0

(r - s)(r + s + 1)/2 MOD n = 0

(r - s)(r + s + 1) MOD 2n = 0 (nota: anche 2n è una potenza di 2)

Dato che: 1 <= r,s <= n-1, si ha che:

r - s < n

r + s + 1 < 2n

Siccome abbiamo supposto che n sia una potenza di 2 e siccome entrambi i fattori (r - s)(r + s + 1) sono minori di 2n si può concludere che devono essere entrambi pari. Infatti, se uno di essi fosse dispari, allora l'altro dovrebbe essere un multiplo di 2n.

Ma ciò non è possibile, poiché se (r - s) è pari, allora (r + s + 1) è dispari e viceversa.

Perciò l'ipotesi fatta per assurdo non è valida e con questo abbiamo dimostrato che tutti i bambini tranne l'ultimo ricevono una caramella nei primi n-1 turni.

E il bambino n-esimo, quando riceverà la sua prima caramella? Se n = 2^p, la (2^p+1-1)-esima caramella sarà sua! Infatti, se assegniamo a k il valore (2^p+1-1), otteniamo:

(k(k+1)/2) MOD n = 2^p(2^p+1 - 6) MOD 2^p = 0.

La dimostrazione di Francesco Veneziano
Consideriamo per ora infiniti bambini messi in fila e numerati a partire da 0.
La maestra da' le caramelle ai numeri 0-2-5-9-14...
E' facile dimostrare per induzione che la maestra da' la caramella k-esima al bambino (k-1)(k+2)/2, infatti
(k-1)(k+2)/2 + k + 1 = k(k+3)/2

Supponiamo ora di avere solo N bambini, e che questi siano messi in cerchio, la formula rimane valida ma deve essere valutata modulo N, ed il nostro problema e' sapere se al variare di k tra gli interi positivi la quantita'
(k-1)(k+2)/2 assume tutti i possibili resti modulo N.

Chiamiamo f(k)=(k-1)(k+2)/2

Si osserva subito che f(k) == f(k+2N) (mod N) e quindi dobbiamo far assumere a k i valori tra 1 e 2N.
Inoltre f(k)==f(-k-1) (mod N) e quindi possiamo far assumere a k solo i valori tra 0 e N-1, dato che i valori tra N e 2N-1 si ripetono simmetricamente.
Ci siamo dunque riportati allo studio della surgettivita' di una funzione a valori in Z/NZ

Siamo pronti per dimostrare che se N>1 e' dispari qualche bambino non riceve caramelle.
Se N=3 f(k)==2k^2+2k-1 (mod 3) che non vale mai 1.
Se N>3, poiche' N e' dispari 2 e' invertibile modulo N e quindi f(k) assume tutti i valori modulo N se e solo se li assume (k-1)(k+2), e questa funzione non puo' assumerli perche' vale 0 sia in 1 che in N-2.

Se con N bambini ognuno riceve caramelle, questo avverra' anche se i bambini sono in numero che divide N, perche' se vengono raggiunte tutte le classi di resto modulo N lo stesso vale per le classi di resto modulo un suo divisore;
abbiamo quindi dimostrato che se N NON e' una potenza di 2, qualche bambino non riceve caramelle.

Dimostriamo ora per induzione che se N e' una potenza di 2 tutti i bambini ricevono delle caramelle.
Se N=1 e' evidente, supponiamo che per N=2^m ogni bambino riceva caramelle, cioe' che f(k) assuma tutti i resti modulo 2^m.
Si verifica che f(2^(m+1)-1-k)== f(k) + 2^m (mod 2^(m+1)) e quindi che mentre k varia da 0 a 2^m-1 f(k) assume tutte classi distinte per ipotesi induttiva, e mentre varia da 2^m a 2^(m+1)-1 assume specularmente le classi rimanenti,
QED.

(salvo sviste ed errori vari)

5. Altri problemi simili
In questo articolo vorrei presentarvi una classe di problemi aritmetici che hanno attirato la mia attenzione per la loro somiglianza con i mandala. Con opportune semplificazioni possono essere proposti anche ad alunni di 11-14 anni.

Rifornimenti in un percorso circolare

Un'automobile deve percorrere in senso antiorario un circuito circolare. Il suo serbatoio è inizialmente vuoto. Sulla pista è però presente l'esatta quantità di carburante necessaria al percorso distribuita in 3 parti non necessariamente uguali.

Dimostrare che, comunque si dispongano i 3 rifornimenti nel circuito, esiste sempre un punto dal quale l'automobile può partire e completare l'intero giro.

Si provi a generalizzare la proposizione al caso di n rifornimenti.

Questo problema è stato proposto al Forum del Progetto Olimpiadi della matematica, il 25-07-2004 e al SIG GIOCHI del Mensa Italia. E' stato assegnato agli esami di ammissione al primo anno di ingegneria dell'Università Normale di Pisa.

Sette elfi e tre litri di latte

Sette Elfi siedono intorno ad una tavola rotonda.

Ciascun elfo ha una tazza.

In alcune tazze c'é un po' di latte.

Ciascun elfo, a turno, in senso orario, divide tutto il suo latte in sei parti uguali fra le tazze degli altri sei elfi.

Dopo che il settimo elfo ha compiuto questa operazione, ogni tazza contiene esattamente tanto latte quanto ne conteneva all'inizio.

Quanto latte c'è in ogni tazza, se all'inizio c'erano in tutto tre litri di latte?

Si supponga che in tutti i travasi non si sia persa neppure un goccia di latte.

Questo problema è tratto dalla collezione "The problems of the All-Soviet-Union mathematical competitions 1961-1986", nella versione inglese di Vladimir A. Pertsel. In particolare, il problema è stato assegnato alla "11-th competition -- Tallinn, 1977".

Uomini in cerchio

Alcuni uomini erano seduti in cerchio, sicchè ciascuno di essi aveva due vicini; e ciascuno di essi aveva un certo numero di scellini.

Il primo aveva uno scellino in più del secondo, che aveva uno scellino in più del terzo, e così via.

Il primo diede uno scellino al secondo, che diede due scellini al terzo e così via, ciascuno dando uno scellino in più di quanto ricevuto, fintanto che fu possibile.

Alla fine, c'erano due vicini uno dei quali aveva 4 volte più scellini dell'altro.

Quanti uomini c'erano? E quanto aveva inizialmente quello più povero?

Questo problema è tratto Lewis Carroll, Pillow Problems, ...

Il problema di Josephus Flavius

Dieci soldati Giudei, incalzati dall'esercito Romano, si rifugiano in una grotta.

I nemici li scoprono e stanno per attaccare. I dieci soldati sanno che se saranno catturati dovranno subire terribili sofferenze prima di essere uccisi.

Piuttosto che cadere nelle mani dei Romani, decidono di uccidersi a vicenda, uno alla volta fino all'ultimo sopravvissuto il quale dovrà suicidarsi.

Si dispongono in cerchio e procedono così: il 1° uccide il 2°, il 3° uccide il 4° e così via.

Procedendo sempre nello stesso senso, chi sarà l'ultimo a morire?

Il problema di Josephus può apparire un po' macabro ma ha una lunghissima tradizione matematica ed alcune versioni sembrano essere ispirate da fatti storici realmente accaduti come le decimazioni di guerra e la punizione dei disertori.

Il famoso medico e matematico Gerolamo Cardano, nel 1539 fu il primo ad identificare il sopravvissuto con l'ebreo Josephus Flavius (37-100), autore del De bello Judaico.

La storia è ambientata in Palestina, nell'anno 67. E' in pieno svolgimento la guerra tra i Romani e i Giudei, che si concluderà con la distruzione di Gerusalemme.

Il DECIMAL BASIC è un interprete BASIC creato da Shiraishi Kazuo. Può essere interessante per i matematici perché, tra l'altro, gestisce i numeri fino a 5000 cifre significative.

Assieme all'editor, al debugger e a tutto l'ambiente di sviluppo occupa meno di 700 Kb di memoria e può essere scaricato liberamente alla pagina: http://hp.vector.co.jp/authors/VA008683/english/

NOTA.
Il problema delle caramelle è stato tratto dall'APMO 1991. Ecco la versione originale.
1991 Asian Pacific Mathematical Olympiad
During a break, n children at school sit in a circle around their teacher to play a game. The teacher walks clockwise close to the children and hands out candies to some of them according to the following rule. He selects one child and gives him a candy, then he skips the next child and gives a candy to the next one, then he skips 2 and gives a candy to the next one, then he skips 3, and so on. Determine the values of n for which eventually, perhaps after many rounds, all children will have at least one candy each.

luglio 2004

Sito Web realizzato da Gianfranco Bo