
[BASE Cinque - Appunti di Matematica ricreativa]
Breve storia della primalità di 1
Cari colleghi docenti di matematica, noi tutti insegniamo che il più piccolo numero primo è 2 e spieghiamo perché non conviene considerare 1 come numero primo.
Tuttavia ancora oggi c'è un po' di confusione su questo argomento a vari livelli scolastici, perfino nei test di ammissione ad una facoltà universitaria (non matematica).
Allora, come dovremmo comportarci con i nostri studenti di scuola media e superiore?
Credo che per assumere l'atteggiamento più giusto sia importante conoscere la storia della primalità di 1.
Ho preparato un breve riassunto basandomi sull'articolo di Chris K. Caldwell e Yeng Xiong, "What is the Smallest Prime?", in Journal of Integer Sequences, Vol. 15 (2012).
---
Immaginiamo dunque di chiedere ai grandi matematici della storia:
"Si può dire che 1 è un numero primo?"
Le risposte sarebbero...
1. Euclide (-300)

Non rispondo a domande cretine!
Euclide, nel libro VII degli Elementi definisce l'unità, il numero e il numero primo.
Dalle definizioni risulta chiaramente che l'unità non fa parte dei numeri. Euclide perciò non ritenne opportuno dire esplicitamente che l'unità non è un numero.
2. Nicomaco di Gerasa (100)

Per Nicomaco, Giamblico (300), Cassiodoro (550), Boezio (500), e altri matematici dell'epoca, i numeri primi erano un "sottoinsieme" dei numeri dispari, perciò 2 non era considerato primo.
3. Isidoro di Siviglia (600)

Euclide ha detto implicitamente che 1 non è un numero, perciò non ha senso chiedersi se è primo.
L'unità è il seme di tutti i numeri ma non è un numero.
Sono passati 900 anni e almeno questo dovreste averlo capito, dico bene?
4. Simon Stevin (1585)

1 è un numero.
Se non lo fosse allora dovremmo ammettere che 3 + 1 = 3 e nessuno lo ammette.
Detto questo, non me ne frega niente se 1 è primo o no. I numeri mi servono per esprimere delle quantità.
Nel suo libretto De Thiende del 1585, sdogana 0 e 1 come numeri.
Def. 1. L'Aritmetica è la scienza dei numeri.
Def. 2. Numero è ciò che esprime la quantità di ciascuna cosa.
Def. 3. I segni con cui si rappresentano i numeri sono 10 e cioè, 0 che è l'inizio dei numeri, 1, 2, 3, 4, 5, 6, 7, 8, 9.
5. Marin Mersenne (1625)

Ok, 1 è un numero ma secondo me non è primo.
Mersenne, nel suo libro La Verité des sciences, 1625 scrive:
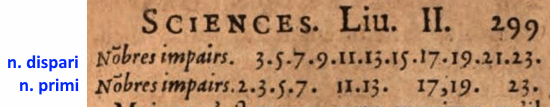
6. Christian Goldbach (1742)

Anche secondo me 1 è primo.
Ehi ragazzi, mi sembra che ogni numero pari si possa scrivere come somma di due numeri primi!
Chi lo dimostra?
Il seguente frammento, tratto da una lettera che Goldbach scrisse a Euler, mostra le scomposizioni dei numeri 4, 5, e 6 in numeri primi.
E' evidente che 1 è un numero primo.
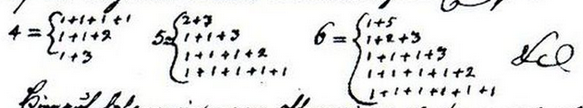
7. Leonhard Euler (1770)

Dài, non scherzate!
1 non è primo.
8. Carl Friedrich Gauss (1801)

Mi fa comodo stabilire che 1 non è primo.
Così riesco a scrivere in modo più semplice il mio Teorema fondamentale dell'Aritmetica.
Teorema Fondamentale dell’Aritmetica. Ogni numero naturale maggiore di 1 o è un numero primo o si può esprimere come prodotto di numeri primi. Tale rappresentazione è unica, se si prescinde dall’ordine in cui compaiono i fattori.
9. Leopold Kronecker (1901)

1 è primo.
10a. Godfrey Harold Hardy (1933)

1 è primo.
Nel suo libro A Course of Pure Mathematics, 1908-1933 inizia così la dimostrazione per assurdo che esistono infiniti numeri primi:
Se esiste soltanto un numero finito di primi, siano 1, 2, 3, 5, 7, 11, ..., N.
Consideriamo allora il numero 1 + (1·2·3·5·7·11·...·N).
...
10b. Godfrey Harold Hardy (1938)

Ho cambiato idea.
1 non è primo.
Nel suo libro A Course of Pure Mathematics del 1938 inizia così la dimostrazione per assurdo che esistono infiniti numeri primi:
Siano 2, 3, 5, 7, 11, ..., pN tutti i numeri primi fino a pN.
Sia P = (2·3·5·7·11·...·pN)+1.
...
Tutta questa storia mi sembra un po' maschilista. Possibile che nessuna donna matematica si sia mai pronunciata sulla primalità di 1? Non lo so.
Perciò concludo con un finale a modo mio.
11. Ada Lovelace

Cari maschietti, volete finirla con questa tiritera?
1 non è primo. Punto.
L'articolo citato sopra, Chris K. Caldwell, Yeng Xiong, "What is the Smallest Prime?", in Journal of Integer Sequences, Vol. 15 (2012) è disponibile online qui: https://cs.uwaterloo.ca/journals/JIS/VOL15/Caldwell1/cald5.pdf
Oggi, la definizione di "numero primo" è fatta in modo da escludere 1.
Ecco alcuni esempi. Scegliete quella che vi piace di più oppure dite la vostra.
I numeri interi positivi >1 che non sono primi, si dicono composti.
Il numero 1 non è né primo né composto.
Quindi abbiamo, per esempio:
Perché "conviene" che 1 NON sia primo?
Il motivo più evidente è che se 1 fosse primo, allora la fattorizzazione in numeri primi non sarebbe più unica e il teorema fondamentale dell'Aritmetica non sarebbe più valido. Dovremmo modificarlo togliendo l'unicità. Così perderebbe molto interesse.
In alternativa dovremmo modificarlo escludendo 1 dalla fattorizzazione in numeri primi. Così perderebbe molta eleganza.
Perché se 1 fosse primo allora la fattorizzazione in primi non sarebbe più unica?
Perché, per esempio:
12 = 1·22·3
12 = 12·22·3
12 = 13·22·3
e così via...
In un test di ammissione alla facoltà di Veterinaria del 2018 si legge il seguente quesito a risposta multipla:
---
A Giorgio viene chiesto di continuare la sequenza:
1 – 2 – 4 – 7 – 12 – 19 – 30 – …
Qual è il prossimo numero che Giorgio dovrà inserire?
A) 42
B) 43
C) 47
D) 52
E) 53
---
Prima di procedere, date la vostra risposta.
.
.
.
.
.
Secondo i progettisti del test, la risposta "attesa" è la B) 43 perché:
Ciascun numero della sequenza si ottiene dal precedente sommando un numero primo (ossia i numeri divisibili solo per sé stessi e per l’unità) in progressione partendo da 1, ossia i numeri 1, 2, 3, 5, 7, 11 e infine 13.
Beh, ogni quesito del tipo "continua la sequenza..." può avere diverse soluzioni "interessanti" perciò il vero problema è indovinare quella che si aspetta chi te lo propone.
In questo caso specifico, il candidato avrebbe potuto cavarsela con lil seguente ragionamento:
Ciascun numero della sequenza si ottiene dal precedente sommando un numero non composto in progressione partendo da 1, ossia i numeri 1, 2, 3, 5, 7, 11 e infine 13.
Cari colleghi la storia della primalità di 1 ci insegna due cose importanti che dovrebbero entrare nel nostro stile didattico. Ve le propongo assieme a due citazioni.
---
Pace e bene a tutti.
GfBo
Data creazione: luglio 2020
Ultimo aggiornamento: agosto 2020
html5
Sito Web realizzato da Gianfranco Bo