[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Paravia,Torino, 1925
In tutti i tempi, e presso tutti i popoli, si insegnavano dei giochi per
rendere dilettevole e meno noiosa l'aritmetica.
Saggiamente questi giochi si trovano nei nuovi programmi delle scuole
elementari. Credo far cosa utile agli insegnanti col pubblicarne alcuni.
1. Quadrato Magico
Nel quadrato qui sotto sono scritti i numeri 1,2,3, ...9. Si verifichi che la
somma dei numeri scritti su d'una stessa orizzontale, o su d'una stessa
verticale, o su una delle due diagonali, è sempre 15, e cioè 2 + 7 + 6 = 9 + 5
+ 1 = 4 + 3 + 8 = 2 + 9 + 4 = 7 + 5 + 3 = 6 + 1 + 8 = 2 + 5 + 8 = 4 + 5 + 6 =
15.
| 2 | 7 | 6 |
| 9 | 5 | 1 |
| 4 | 3 | 8 |
Sono tutte le scomposizioni di 15 nella somma di tre numeri 1, 2, ...9. I numeri 1, 3, 7, 9 entrano in due somme, i numeri 2, 4, 6, 8 in tre, e il 5 entra in quattro somme. Gli antichi Magi di Persia, che erano anche medici, curavano le malattie applicando sulla parte inferma un quadrato magico, seguendo il principio di medicina, ed anche di didattica: primum non nocère, primo principio: non nuocere. Questi quadrati erano pure noti agli antichi Cinesi, agli Indiani e Arabi verso l'anno 800 ed in Europa verso il 1300. Servono nella scuola come esercizio di addizione.
2.
I numeri da 1 a 16 sono disposti in questo quadrato, in modo che si ottiene
sempre 34 sommando i numeri di una stessa orizzontale, o d'una stessa verticale,
o d'una diagonale; o anche sommando in altri modi quattro numeri della tabella;
per es. 1 + 14 + 7 + 12 = 34; 1 + 6 + 16 + 11 = 34, in 86 modi diversi.
| 1 | 14 | 4 | 15 |
| 12 | 7 | 9 | 6 |
| 13 | 2 | 16 | 3 |
| 8 | 11 | 5 | 10 |
3.
Dispongo i numeri da 1 a 6 sui vertici e lati di un triangolo, come nella figura
La somma dei numeri che stanno su d'un medesimo lato, vale 11; cioè 2 + 3 + 6 =
2 + 5 +4 = 6 + 1 + 4 = 11. Questo triangolo, come il seguente, dicesi magico.
| 2 | ||||
| 3 | 5 | |||
| 6 | 1 | 4 |
4.
La somma dei numeri scritti su di uno stesso lato di questo triangolo vale 20.
La somma del numero scritto in un vertice coi quattro numeri vicini vale 25. La
somma dei due numeri medi di un lato, meno il numero del vertice opposto vale 5.
La somma dei quadrati dei numeri d'uno stesso lato vale 126.
| 8 | ||||||
| 7 | 1 | |||||
| 3 | 6 | |||||
| 2 | 9 | 4 | 5 |
5. Tavole misteriose
Pensa un numero da 1 a 15, e dimmi in quali delle seguenti tavole esso si
trova:
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 |
| 2 | 3 | 6 | 7 | 10 | 11 | 14 | 15 |
| 4 | 5 | 6 | 7 | 12 | 13 | 14 | 15 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Il numero pensato è la somma dei primi numeri delle tavole in cui si trova. Le tavole si costruiscono in questo modo: Si scrive 1 in capo alla prima, e 2 in capo alla seconda; poi 3 = 2+1 si scrive nelle tavolette comincianti con 2 ed 1;poi 4 si scrive a capo della terza tavola; 5 = 4 + 1 si scrive nelle tavole comincianti con 4 ed 1; 6 = 4 + 2 si scrive nelle tavole con 4 e 2; 7 = 4 + 2 + 1 nelle tavole con 4, 2, 1; poi 8 a capo di una nuova tavola; e così via.
Così si chiamano alcuni problemi, in cui la risposta vera non è quella che prima si presenta alla mente. Sono dilettevoli, ed acuiscono la mente. Molti di questi problemi sono estratti da una raccolta della prof.ssa P. QUARRA, in Bollettino di Matematica, del prof. Conti, a. 1919.
6.
Si ha una fune lunga metri 7 e se ne taglia ogni giorno un metro. Dopo quanti
giorni la fune sarà tagliata? RISPOSTA: Dopo 6 giorni (e non 7).
7.
Si hanno 14 soldati in fila. La distanza fra un soldato e l'altro è di metri 3.
Quale è la distanza dal primo all'ultimo soldato?
RISPOSTA: m. 3 x13. Il problema è simile al precedente.
8. Importanza dello zero.
Un tale scrive ad un venditore di animali: "mandatemi 1 o 2 gatti".
Dopo qualche giorno si vede arrivare una grossa gabbia, piena di gatti,
accompagnata da una lettera del venditore che diceva: "per ora vi mando 58
gatti; la settimana prossima manderò gli altri 44".
Donde è nato l'equivoco?
9.
Una lumaca si arrampica lungo un muro alto 5 metri. Ogni giorno sale tre metri e
ogni notte discende 2 metri.
Dopo quanti giorni la lumaca avrà raggiunto la cima del muro?
RISPOSTA: Dopo 3 giorni ( e non dopo cinque).
10.
In uno scaffale erano disposti per ordine i tre volumi di Dante, ognuno di 100
fogli. Un tarlo cominciò a rodere il primo foglio del primo volume e procedendo
diritto, finì col rodere l'ultimo foglio dell'ultimo volume. Quanti fogli egli
rose?
RISPOSTA: 102, perché i volumi sono ordinati da sinistra a destra, e i fogli
dei volumi risultano ordinati da destra a sinistra; il primo foglio del primo
volume è adiacente al secondo volume, come pure l'ultimo foglio del terzo
volume.
11.
Ogni minuto dal centro di una città parte una vettura che va alla stazione
in 7 minuti e poi ritorna. Una vettura che va dal centro alla stazione quante
vetture incontrerà?
RISPOSTA: 13 ( e non 7 né 14); poiché 14 sono le vetture che fanno servizio, e
una di esse incontra le altre 13.
12.
Si stima che la superficie del capo umano portante capelli è di 775 cm2 e
che ogni cm2 contiene al massimo 165 capelli. Dimostrare che in una città di
150 000 abitanti vi sono due persone che hanno lo stesso numero di capelli.
RISPOSTA: Il massimo numero di capelli che può avere una persona é 775 x 165 =
123 875 < 150 000.
13.
Due fratelli avevano insieme 40 soldi; se li divisero; il primo con 20 soldi
compera delle uova ad 1 soldo l'uno e le vende a 2 soldi; il secondo compra
delle uova a 2 soldi l'uno e li rivende a 1 soldo; poi rimettono insieme i loro
soldi. Hanno guadagnato? RISPOSTA: Guadagnarono 10 soldi. Questo problema, con
altri seguenti, trovasi nel General Trattato di numeri et misure, di TARTAGLIA,
illustre matematico, nato a Brescia nel 1506, morto a Venezia nel 1557.
14.
Due piroscafi A e B sono partiti insieme per un viaggio di 6000 miglia
all'andata e altrettanti al ritorno. Il piroscafo A mantiene una velocità di 8
miglia all'ora nell'andata e 12 miglia all'ora nel ritorno; il piroscafo b
mantiene una velocità costante di 10 miglia all'ora. Arrivano essi insieme al
luogo di partenza?
RISPOSTA: B precede A di 50 ore.
15.
Una fruttivendola vende 30 pere a 3 per un soldo e poi 30 pere a 2 al soldo.
Un'altra vende 60 pere a 5 per 2 soldi. Chi ha ritirato di più?
RISPOSTA:Ha ritirato di più la prima, la quale ritirò 25 soldi, mentre la
seconda ne ritirò 24.
16.
Di due commessi, l'uno riceve £ 1000 alla fine di ogni mese con l'aumento di £
20 dopo ogni mese di servizio. Un altro riceve £ 500 alla quindicina con
l'aumento di £ 5 ogni quindicina. Chi guadagna di più?
RISPOSTA: Il secondo guadagna 5 lire al mese di più del primo.
17.
Due viaggiatori, uno dei quali ha 5 pani e l'altro 7 pani, ne incontrano un
terzo affamato, che li invita a dividere seco lui la loro provvista. I tre
viaggiatori mangiano insieme ed il terzo sopraggiunto, accomiatandosi dalla
compagnia, lascia come retribuzione di quanto è stato a lui ceduto, 12 monete.
Come dovranno essere divise le monete fra i due compagni?
RISPOSTA: Le monete si dovranno ripartire in parti proporzionali ai numeri 1 e
3. Questo problema, con altri simili, si trova nel Liber Abaci di LEONARDO
PISANO, filio Bonacii, anno 1202, pag. 283.
18.
Un Arabo morendo lasciò ai suoi tre figli 17 cammelli in eredità e ordinò che
la metà di essi fosse data al primo figlio, la terza parte al secondo, e la
nona al terzo figlio. I tre figli si rivolsero per la divisione al cadì, il
quale enne con il proprio cammello, che unì agli altri. Diede la metà dei 18
cammelli, cioè 9 al primo, un terzo, cioè 6 al secondo, un nono, cioè 2 al
terzo figlio, e poi, ripreso il suo cammello se ne andò ringraziato dai tre
figli, ognuno dei quali aveva ricevuto più di quanto gli spettava. Spiegare
l'enigma.
RISPOSTA: Infatti, 1/2 + 1/3 + 1/9 < 1, cioè quel padre non distribuì tutta
l'eredità.
19.
Le tre Grazie portando pomi, ognuna lo stesso numero, incontrano le nove Muse, e
con loro dividono i pomi, sicché tutte hanno lo stesso numero di pomi. Quanti
erano i pomi?
RISPOSTA: 12 o un suo multiplo. Questo problema è estratto dall'Antologia
greca; questo libro, dei tempi dell'imperatore Traiano, morto nell'anno 117,
contiene in versi greci vari problemi, alcuni antichissimi.
20.
Le nove Muse, portando ognuna lo stesso numero di corone, incontrano le tre
Grazie e loro distribuiscono delle corone, e tutte ne hanno lo stesso numero.
Quante corone?
RISPOSTA: un multiplo di 9 e di 12, cioè di 36.. Dall'Antologia greca.
21.
Una contadina porta delle uova al mercato. Sa che contandole a 2 a 2 ne avanzava
1, contandole a 3 a 3 ne avanzava 1, a 4 a 4 ne avanzava 1, a 5 a 5 ne avanzava
1, a 6 a 6 ne avanzava 1 e contandole a 7 a 7 aveva un numero esatto. Quante
uova?
RISPOSTA: 301, ovvero 301 più un multiplo di 420. Così Leonardo Pisano, pag.
281.
22.
Una donna porta delle uova al mercato; ad un primo compratore vende la metà
delle uova più mezzo uovo, ad un secondo vende la metà delle uova rimaste più
mezzo uovo, ad un terzo vende la metà delle uova rimaste più mezzo uovo; così
ha venduto tutte le uova che possedeva. Quante uova possedeva?
RISPOSTA: 7 uova. Se, in una scuola, questo problema, od altri, è troppo
difficile, si inverte: " Una donna portò 7 galline al mercato; ad un primo
compratore vendette la metà delle galline più mezza gallina. Quante ne sono
rimaste? ecc.".
23.
Una comitiva di 7 viaggiatori si presenta ad un albergo, e domanda un letto per
ogni viaggiatore. L'oste risponde: ho solo sei letti, distinti colle lettere A,
B, C, D, E, F. Ma guarderò di aggiustarvi. Perciò destinò due viaggiatori a
dormire nel letto A, poi uno nel letto B, e fa tre; poi uno in C, e conta
quattro; poi uno in D, e conta cinque; poi uno in E, e conta sei; poi prende uno
di quelli che erano in A e lo conduce in F, e conta sette. Così i 7 viaggiatori
dormono in 6 letti, uno per letto.
Come ha fatto? Chi fa il gioco, rappresenta i letti con sei carte, e procede
rapido, onde l'uditore non si accorga che un viaggiatore è stato contato due
volte.
24.
In un bicchiere si trova del vino, e in un altro dell'acqua. Si prende un
cucchiaio di vino dal 1° e si versa nel 2°, si mescola questo, poi si prende
un cucchiaio del liquido del 2° bicchiere e si versa nel 1°.
La quantità di vino che si porta dal 1° nel 2°, è più grande o più piccola
di quella dell'acqua portata nel 1°?
Molte persone rispondono che la prima quantità è più grande. Invece sono
uguali. Invero, essendovi dopo l'operazione, la stessa quantità nei due
bicchieri, è necessario che tanto sia passato dal 1° nel 2°, quanto dal 2°
al 1°.
25.
Due persone hanno una botte con 8 litri di vino; e due botti vuote capaci di 5 e
3 litri. Vogliono dividere gli 8 litri in parti uguali.
Nelle tre botti, capaci di litri 8 5 3
Sonvi all'inizio litri di vino 8 0 0
Verso il 1° nel 3°; ho litri 5 0 3
Verso il 3° nel 2°; ho litri 5 3 0
Verso il 1° nel 3°; ho litri 2 3 3
Verso il 3° nel 2°; ho litri 2 5 1
Verso il 2° nel 1°; ho litri 7 0 1
Verso il 3° nel 2°; ho litri 7 1 0
Verso il 1° nel 3°; ho litri 4 1 3
Verso il 3° nel 2°; ho litri 4 4 0
Che è la soluzione data da Tartaglia, libro 16, N. 132.
26.
Problema del lupo, della capra e del cavolo.
(TARTAGLIA, libro 16, N. 141).
Un tale ha con sè un lupo, una capra e un cavolo; e deve traversare un fiume,
con una barca, in cui può portare un sol .. oggetto per volta. Egli vuoI
traversare col cavolo, ma la capra gli dice: non lo fare che il lupo mi mangia.
Egli vuoI traversare col lupo, ma il cavolo gli dice: non lo fare che la capra
mi mangia. Come farà?
Traghetta la capra, poi il cavolo, e riporta la capra, traghetta il lupo, e
infine la capra; e così ha salvato capra e cavolo. "e da questo è
nasciuto un certo proverbio fra gli huomini, dicendo in qualche proposito, egli
ha salvato la capra e i verzi (cavoli) “.
27.
Un negoziante aumenta del 20 per 100 i prezzi segnati sulle sue merci; poi
mediante un avviso, dice di concedere ai suoi avventori lo sconto del 20 per 100
sui prezzi segnati. Quale sconto egli fece sui prezzi primitivi?
RISPOSTA: Il 4 per 100.
28.
Pietro, che possiede 1024 lire, si mette a giocare alla pari cioè, se
vince, guadagna una somma pari alla puntata. Egli gioca 10 partite, e punta
sempre la metà del denaro che possiede. In fine egli ha guadagnato 5 partite e
perdute 5. Avrà egli guadagnato?
RISPOSTA: Egli ha perduto 781 lire, oltre il tempo.
29.
1 X 1 = 1
11 X 11 = 121
111 X 111 = 12321
1111 X 1111 = 1234321
11111 X 11111 = 123454321
Ibn Albanna, matematico arabo, vivente al Marocco verso il 1200, pubblicò
queste moltiplicazioni curiose, e le seguenti.
30.
12345679 X 9 = 111 111 111
12345679 X 8 = 98765432.
31.
1 X 9 + 2 = 11
12 X 9 + 3 = 111
123 X 9 + 4 = 1 111
1234 X 9 + 5 = 11 111
12345 X 9 + 6 = 111 111
123456 X 9 + 7 = 1 111 111
1234567 X 9 + 8 = 11 111 111
12345678 X 9 + 9 = 111 111 111
32.
1 X 8 + 1 = 9
12 X 8 + 2 = 98
123 X 8 + 3 = 987
1234 X 8 + 4 = 9876
12345 X 8 + 5 = 98765
123456 X 8 + 6 = 987654
1234567 X 8 +7 = 9876543
12345678 X 8 + 8 = 98765432
123456789 X 8 + 9 = 987654321
33.
9 X 9 + 7 = 88
9 X 98 + 6 = 888
9 X 987 + 5 = 8888
9 X 9876 + 4 = 88888
9 X 98765 + 3 = 888888
9 X 987654 + 2 = 8888888
9 X 9876543 + 1 = 88888888
9 X 98765432 + 0 = 888888888.
34.
Disposizione particolare delle cifre1, 2,....... 9:
2 X 78 = 156 = 39 X 4
35.
9 = 97524/10836
= 95823/10647
= 95742/10638
= 75249/08361
= 58239/06471
= 57429/06381.
In ognuna di queste espressioni di 9 figurano tutte le cifre, ognuna una volta
sola.
36.
Dividere il numero 100 in quattro parti, in modo che la prima più 4,
eguagli la seconda meno 4, e la terza moltiplicata 4, e la quarta divisa 4.
100 = 12 + 20 + 4 + 64
12 + 4 = 16
20 - 4 = 16
4 X 4 = 16
64 / 4 = 16.
37.
Moltiplica un numero di più cifre per 1000; addiziona il prodotto al numero
dato; dividi la somma per 7, poi per Il, poi per 13. Ritroverai il numero dato.
38.
Theone da Smirne, che visse verso il 100, Boezio morto nel 525, ed altri,
chiamano numeri sferici, i numeri i cui quadrati terminano colle stesse cifre.
Esempi:
52 = 25
62 = 36
252 = 625
762 = 5776
6252 = 390625
3762 = 141376
906252 = 8212890625
93762 = 87909376
39.
Numeri ciclici.
Il numero 142857 moltiplicato per 2, 3, 4, 5, 6, dà i prodotti 285114,
428571, 571428, 714285, 857142 contenenti le stesse cifre, permutate in ordine
circolare. Esso moltiplicato 7 vale 999999.
40.
Il numero di 18 cifre: 052 631 578 947 368 .(21 moltiplicato per 2, 3,
...18, dà sempre le stesse cifre permutate in circolo. Esso vale (1018-1)/19.
I numeri ciclici sono anche detti "numeri della Fenice., perché si
riproducono per moltiplicazione, come la favolosa araba fenice. Queste cifre
sono il periodo di 1/19 sviluppato in frazione decimale.
In generale, i numeri cicli ci si ottengono da10n-1) /n. attribuendo ad n i
valori, 7, 17, 19, 23, 29, 47, 59, 61,97, 109, 130, 149... Qui si può vedere un
teorema di Fermat, o lo sviluppo d'una frazione ordinaria in frazione decimale
periodica.
41.
Un topo generò 7 topi; ognuno di questi altri 7 i topi; ognuno di questi
altri 7; e ognuno di questi altri 7. Quanti topi in tutto?
RISPOSTA: 1 + 7 + 72 + 73 + 74 = 2801.
Questo problema è liberamente tradotto dal papiro egiziano di AHMES, di 4000
anni fa.
42.
“Septem vetulae vadunt Romam; quarum quaelibet, habet burdones 7;
et in quolibet burdone sunt sacculi 7;
et in quolibet sacculo panes 7;
et quilibet panis habet cultellos 7;
et quilibet cultellus habet vaginas 7.
Quaeritur somma omnium praedictorum.“
(LEONARDO, pag. 311). Sommando le 7 vecchierelle colle 49 vesti, colle 343
saccocce, coi 2401 pani, coi 16 807 coltelli e colle 117 649 buste, si hanno 137
256 oggetti. Questo problema, in sostanza identico al precedente, ed ancora
popolare al giorno d'oggi, conduce alle progressioni geometriche. La regola per
la loro somma si trova in Euclide, libro IX, prop. 35.
43.
Il Maestro, e i piccoli allievi Pietro e Paolo.
MAESTRO: Pietro, pensa un numero.
PIETRO: Pensato.
MAESTRO: Aggiungi uno.
PIETRO: Aggiunto.
MAESTRO: Quanto hai trovato?
PIETRO: Sei.
MAESTRO: Tu Paolo, indovina il numero pensato da Pietro.
PAOLO: 6 -1 = 5, tale è il numero pensato.
MAESTRO: Bravo Paolo, hai fatto un primo passo in Algebra.
44.
Gli stessi.
MAESTRO: Paolo, pensa un numero, raddoppialo, aggiungi 3, dicci il risultato, e
tu Pietro indovina il numero pensato.
PAOLO: 15.
PIETRO: (15 -3) / 2 = 6.
MAESTRO: Bravo Pietro, hai fatto un lungo passo nell'Algebra.
45.
Pensa un numero, raddoppialo, aggiungi 8, dividi per 2, sottrai il numero
pensato; avrai 4.
46.
Pensa un numero, moltiplica per 2, aggiungi 5, moltiplica per 5, aggiungi10,
e moltiplica per10, e dimmi il risultato. Se da questo sottraggo 350, e divido
per 100, ho il numero pensato. Se esso è n:
(( n X 2 + 5) X 5 +10) X 10-350) / 100 = n. Così LEONARDO, nel capitolo
"de divinationibus".
47.
Scrivi un numero di tre cifre, decrescenti di 1 per volta; capovolgi; fa la
differenza fra i due numeri.
Avrai 198.
ESEMPIO: 987 -789 = 198.
48.
Scrivi un numero di tre cifre decrescenti, inverti l'ordine delle cifre, fa la
differenza dei due numeri, e a questa differenza aggiungi la medesima colle
cifre invertite. Troverai 1089.
ESEMPIO: 763 -367 = 396; 396 + 693 = 1089.
49.
Scrivi un numero di tre cifre, inverti l'ordine i delle cifre, e fa la
differenza dei due numeri, maggiore meno minore. Dimmi l'ultima cifra della
differenza, e ti dirò la differenza.
la cifra media è 9; la prima cifra = 9 - ultima. Se però l'ultima cifra è 0,
la differenza = 0.
50.
Scrivi un numero di più cifre, moltiplica per10, sottrai il primo numero,
cancella nella differenza una cifra non nulla, e dimmi la somma delle rimanenti.
La cifra cancellata più la somma delle cifre rimaste deve essere un multiplo di
9, il che permette di determinarla. Se p. es. la somma è 15, la cifra
cancellata è 3, perché 15 + 3 = 18. La differenza considerata è un multiplo
di 9.
51.
Si dice ad una persona di prendere tre carte, aventi i numeri o punti da 1a10;
poi di moltiplicare il numero della prima carta per 2, aggiungere1, moltiplicare
il risultato per 5, aggiungere il numero della seconda carta, moltiplicare il
risultato per 2, aggiungere1, moltiplicare il risultato per 5, ed aggiungere la
terza carta. Si domanda il risultato finale di tutte queste operazioni.
Se da questo risultato si sottrae 166, si avrà un numero di tre cifre, le quali
aumentate di1, daranno i numeri delle tre carte. Se per esempio il risultato
finale meno 166 vale 237, le carte sono 3, 4, 8.
Questo problema è una complicazione dell'altro troppo semplice: pensa tre
cifre; addiziona la prima moltiplicata per 100 colla seconda moltiplicata per 10
e colla terza. Se il risultato è 348, avrai pensato 3, 4, 8.
52.
"Quidam ivit negotiando Lucam, deinde Florentiam, et reversus est Pisas; et
fecit in unaquaque civitate duplex, et in unaquaque expendidit denarios 12; et
in fine nil remansit ei. Quaeritur quot in prjncjpio habuit". (LEONARDO,
pag. 329).
Questo negoziante pisano, che commerciò in Lucca, poi a Firenze, e in fine
nella sua città, ed ovunque raddoppiò i denarj che aveva ivi riportati, e vi
spese 12 denari, e cosi si trovò con zero, aveva in principio denari 10 e
mezzo.
53.
Un divoto pregò Giove affinché gli raddoppiasse i denari che aveva in tasca, e
gli avrebbe in compenso date 8 lire. Così fu fatto. Allora pregò Venere dello
stesso miracolo e pagò 8 lire; e infine pregò Mercurio che gli raddoppiasse i
denari, e gli pagò le 8 lire; e cosi si trovò possessore di nulla. Quanti
denari aveva in principio?
L. 7. E’ lo stesso problema precedente. Leonardo risolve questo problema in
due modi, colla regola diretta “regula recta”; e colla inversa “regula
versa”.
Colla regola diretta: Chiamiamo cosa (res) il capitale che egli aveva in
principio; lo duplicò ed ebbe 2 cose, pagò 8 lire e gli rimase 2 cose
-8 lire. Lo duplicò la seconda volta, ed ebbe 4 cose -16 lire. Pagò
lire 8, e restò con 4 cose -24 lire. Lo duplicò la terza volta ed ebbe
8 cose -48 lire. Pagò lire 8, e gli rimase 8 cose -56 lire = 0,
onde 8 cose = 56 lire, e cosa = 7 lire.
E questa la soluzione oggi usata in Algebra, salvo che invece di cosa si
scrive x.
Colla regola inversa: Quella persona che pagò la terza volta 8 lire e nulla gli
rimase, prima di pagare aveva 8 lire. E prima che si raddoppiassero per la terza
volta aveva 4 lire, e prima di pagare la seconda volta aveva 4 + 8 = 12 lire, e
prima del secondo raddoppiamento aveva 6 lire, e prima di pagare la prima volta
aveva 6 + 8 = 14 lire, e prima del primo raddoppiamento aveva il capitale
iniziale di 7 lire.
54.
In un cortile sonvi galline e conigli, in tutto 40 teste e 100 gambe. Quante
galline e quanti conigli?
Leonardo risolve problemi simili colla regola araba della doppia falsa
posizione: “Helchataim quidem arabice, latine duarum falsarum positionum
regula interpretatur, per quam fere omnium quaestionum solutio invenitur “.
Poniamo 0 conigli; le galline sono 40, le gambe 80, man-cano 20 per arrivare a
100.
Aumento di l il numero dei conigli: il numero delle galline diminuisce di1, e le
gambe aumentano di 4 -2 = 2.
Divido 20 per 2, ottengo10; dunque 10 sono i conigli, e 30 le galline.
TARTAGLIA, libro 17, scrive il nome arabo sotto la forma Helcataym. Questa
regola semplice è ora poco usata, e sostituita col sistema di due equazioni di
primo grado.
55.
Antonio dice a sua sorella Maria; io ho tanti fratelli quante sorelle. Maria
risponde: io ho due volte più fratelli che sorelle. Quanti figli e quante
figlie in quella famiglia?
RISPOSTA: 4 maschi e 3 femmine.
56.
Gioco.
Di due persone, una dice un numero da 1 a 10, l'altra aggiunge un numero sempre
da 1 a10, la prima aggiunge un numero fra gli stessi limiti, e così via. Chi
prima arriva a dire 100, vince. Come si fa a vincere?
Chi primo dice 89, potrà al colpo successivo dire 100; e per essere certi di
dire 89, basta dire 78, 67, 56, 45,34,23, 12, 1.
57.
Sonvi 3 persone, e 3 monete, una d'oro, l'altra di f argento, e la terza di
rame. Si danno alle tre persone rispettivamente1, 2, 3 granelli, e sul tavolo se
ne lasciano 18. Chi fa il gioco, va in disparte, e invita le tre persone a
prendere una moneta per uno. Poi si prega colui che ha la moneta di oro, a
prendere tanti granelli quanti ne ha in mano; chi ha la moneta d'argento ne
prenda il doppio di quelli che aveva; chi ha la moneta di rame, prenda il
quadruplo dei granelli che gli furono dati.
Allora si contano i granelli rimanenti dei 18. Essi possono essere 1,2,3,5,6,7,
corrispondenti alle 6 permutazioni dei tre oggetti.
Questo problema si trova in TARTAGLIA, libro 16, N. 196. L'autore dà. una
regola mnemonica per ricordare la permutazione.
Altra ne dà BACHET, ed un'altra OUGHTRED, Mathematical recreations, London,
1653.
LEONARO, pag 307, espone problemi simili, e ne dà la soluzione aritmetica, che
si può tradurre come segue:
Chiamo metallo0, metallo1, metallo 2, rispettivamente oro, argento e rame.
Divido (8 -numero dei granelli rimasti) per 3; il quoto è il metallo scelto
dalla terza persona, e il resto è quello della seconda.
Le monete si possono sostituire con un pomo, un fico, una noce.
58.
I bianchi e i neri. -Avendosi 15 pedine (o carte) bianche, e 15 nere, disporle
in circolo, in modo tale che contandole da un punto determinato, e levando ogni
nona pedina, si tolgano tutte le pedine nere.
TARTAGLIA., libro 16, N. 203, dà la soluzione indicata colla frase:
Populeam virgam mater regina tenebat.
Le vocali a, e, i, o, u valgono 1, 2, 3, 4, 5; le consonanti non contano.
Quella frase indica la successione dei numeri 4, 5, 2, 1, 3, 1, 1, 2, 2, 3, 1,
2, 2, 1. Disponendo 4 bianche, 5 nere, 2 bianche, ecc., si avrà la soluzione
richiesta.
BACHET, Problèmes plaisants et delectables qui se font par les nombres,
pubblicato a Lione nel 1613, alla frase latina, sostituisce la francese:
Mort tu ne falliras pas en me livrant le trepas.
Volendo, col levare ogni terza pedina, togliere tutte le!nere, Tartaglia dà la frase:
Egl'è passata Venere amata, che fece la barchetta rea,
cioè bisogna porre 2 bianche, 2 nere, 1 bianca, 1 nera, ecc.,
Questo passatempo può essere utile per far contare ai bambini, ed insegna un
metodo mnemonico per ricordare cifre.
59.
Un padre distribuisce fra i suoi figli i denari di una borsa. Al primo figlio
dà 1 lira e il settimo di ciò che rimane. Al secondo dà 2 lire e il settimo
di ciò che rimane. Al terzo dà 3 lire e il settimo di ciò che rimane. E così
di seguito; e distribuì tutti i denari della borsa, e risultò che, ognuno dei
figli ricevette la stessa somma. Quanti erano i figli e quante le lire nella
borsa?
RISPOSTA. I figli erano 6, e le lire 36. Questo problema si trova in LEONARDO,
pag. 279, ed in molti altri autori.
Se il problema precedente è troppo difficile in una scuola, si inverte: un
padre distribuisce fra i suoi figli 36 lire. Al primo figlio dà 1 lira + 1/7 di
ciò che rimane. Quanto diede al primo figlio? Al secondo diede 2 lire + 1/7 di
ciò che rimase. Quanto diede al secondo figlio? ecc.
In generale, se il padre dà al primo figlio la somma a più 1/n di ciò che
rimane, e al secondo figlio 2a più 1/n del rimanente, ecc., e così
distribuisce tutti i denari in parti eguali, i figli sono n - 1, e la somma
distribuita è (n - 1)2a.
EULERO risolse questo problema, ed altri più difficili.
60.
Quanti chilogrammi pesa un oggetto pesante 1kg. più della metà del proprio
peso?
RISPOSTA: 2 kg.
61.
Qual è la metà dei due terzi, dei tre quarti, dei quattro quinti di un soldo?
RISPOSTA: Era un centesimo.
62.
Una persona fa il giro del mondo, sempre in piedi. Di quanto il cammino della
testa supera il cammino dei piedi?
RISPOSTA: Della circonferenza di raggio l'altezza della persona.
63.
Pensa un numero, moltiplica per 3, aggiungi uno dei numeri 1, 2, 3, ad arbitrio;
moltiplica per 3, aggiungi il numero pensato. Cosa hai trovato?
Se r è il risultato, r quot 10 è il numero pensato.
Nella numerazione romana si usano i segni:
I=1, V=5, X=10, L=50, C= 100, D=500, M=l000.
Questi segni avevano dapprima una forma speciale, quale si trova nella colonna
Duilio, dell'anno 251 a.C., ancora esistente in Roma, ed in altre iscrizioni.
Poi si confusero colle lettere dell'alfabeto. Ogni altro numero si esprime per
addizione coi precedenti, raramente per sottrazione.
ESEMPIO: Boezio, ucciso da Teodorico nell'anno 525, nel suo libro "De
institutione arithmetica", cosi esprime le potenze di 2: I. II. IIII. VIII.
XVI. XXXII. LXIIII. CXXVIII.
Numeri quadrati: I. IIII. VIIII. XVI. XXV. XXXVI. XL VIIII. LXIIII. LXXXI. C.
Numeri cubi: I. VIII. XXVII. LXIIII. CXXV. CCXVI. CCCXLIII.
Il numero 4 è sempre indicato per IIII in tutti i monumenti romani. e nei libri; la forma sottrattiva IV comparisce dopo il 1600. La forma IX si trova raramente nelle antiche iscrizioni. Nei monumenti, i segni rappresentanti numeri erano spesso sopralineati, per distinguerli dalle lettere dell'alfabeto. Ma nei manoscritti si trova sopralineato il numero delle migliaia. Così nelle opere matematiche di Gerberto, che diventò papa, sotto il nome di Silvestro II, dal 972 al 1003, trovasi:
"jugerum pedes vero XXVIII DCCC"
cioè "il jugero, rettangolo di 240 piedi per 120 piedi, vale 28 800
piedi quadrati".
L. VIRIGLIO, I segni numerali romani, "R. Accademia delle Scienze
di Torino" anno 1916, riproduce numerose iscrizioni romane, contenenti
numeri.
Gli antichi per calcolare, si servivano di sassolini, detti in latino "calculi
", onde la nostra parola calcolo, ancorché le pietruzze non si usino più.
nel calcolo algebrico e infinitesimale. Ma si usano ancora utilmente, sostituite
con ciliegie o noci, nelle prime scuole.
Pitagora, che visse dall'anno 570 a. C. al 470 circa, insegnò, per calcolare su
numeri grandi, a dividere una tavola in colonne, intestate uno, dieci, cento,
mille, ecc., e in ogni colonna si scrivevano, o si indicavano con calcoli, le
unità dei varii ordini. Nella "Ars Geometrica", libro che era
attribuito a Boezio, ma che pare del mille, sta scritto: "Pythagorici vero,
ut in omnibus rebus erant ingeniosissimi et subtilissimi, descripserunt sibi
quandam formulam quam ob honorem sui praeceptoris mensam Pythagoream nominabant;
a posterioribus appellatur abacus ".
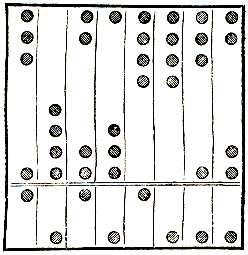
Se le pallottoline sono infilzate in aste, risulta l' ingombrante pallottoliere.
Molto più comoda è la disposizione per cui ogni asta è divisa in due parti:
le pallottole di una parte indicano uno, e sono in numero di 4; nell'altra parte
si trova una pallottola mobile, col valore di 5 (v. figura).

In figura è indicato il numero 64735012.
Questo abaco si è trovato negli scavi di Pompei. È diffusissimo fino dai tempi
più antichi presso i Cinesi, col nome di Suan-pan, o tavola per
calcolare; essi vi eseguiscono tuttora calcoli con grande rapidità e meraviglia
dei viaggiatori Europei.
Di questo abaco parla Lao Tze, contemporaneo di Confucio, a. 500 a. C.
PERNY, Grammaire çhinoise, Paris, 1873, vol. 1, pag. 168, l'attribuisce
a Cheu Ly, anno 2637 a. C.
Si può costruire con una cornice di cm. 10 X 12, del filo e delle perline. Per
facilitare i riporti, alcuni abachi contengono due palline col valore 5, e 5 col
valore 1.
Dalla Cina l'abaco passò in Giappone col nome di Soro.ban, e in Russia,
col nome di S -ciot = calcoli.
Il matematico francese J. V. Poncelet, che fu prigioniero in Russia durante la
guerra napoleonica del 1812-14, vi im- parò l'abaco, e lo importò nelle scuole
elementari francesi. Sarebbe desiderabile una maggiore diffusione di questo
semplice ed utile strumento di calcolo.
Ai nostri tempi, all'abaco si sostituisce la carta quadrettata, che facilita
l'incolonnamento delle cifre ed è utilissima in lunghi calcoli.
Abaco è parola latina, dal greco, e significa "tavola". Il
nome di "tavola pitagorica" passò poi verso il 1600 a significare la
tavola di moltiplicazione.
In Aritmetica si usano segni, o simboli ideografici, rappresentanti idee, e non parole; sono tali le cifre 0, 1,... 9, i segni di operazioni +, -, ..., di relazione =, ecc.
Le cifre 0, 1, 2,... 9 furono introdotte in Europa verso il 1200; noi le imparammo dagli Arabi, e questi dagli Indiani.
Leonardo accompagnò suo padre "publicus scriba", cioè notaio
della repubblica di Pisa, in Bugia, città dell'Algeria; nei suoi viaggi studiò
il "modum indorum ", e nel 1202 scrisse il suo "Liber Abaci
", che comincia colle parole:
" Novem figurae indorum hae sunt 9 8 7 6 5 4 3 2 1. Cum his itaque novem
figuris, et cum hoc signo 0, quod arabice zephirum appellatur, scribitur
quilibet numerus".
La forma delle cifre arabiche è:
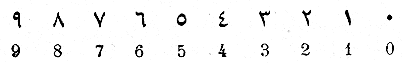
Gli arabi scrivono da destra a sinistra.
La cifra 1 è una sbarra; 2 è una deformazione di =; 3 di =.
La forma delle cifre si fissò dopo l'invenzione della stampa. Lo zero era figurato con un punto dagli Indiani, e lo è ancora dagli Arabi. Il nostro modo di scrivere i numeri con cifre è la rappresentazione sulla carta dell'abaco.
+ "più" e - "meno" comparirono verso il 1500, sostituendo le antiche iniziali di plus e minus.
X "moltiplicato", è generalmente sottinteso fra due lettere, e fra un numero e una lettera. Questo segno con questo significato s'incontra in Oughtred e in Harriot 1631, e usato da Wallis, Newton, ecc. divenne universale.
a/b e (a fratto b) indicano la divisione; questa notazione rimonta agli Indiani, e si trova in Leonardo Pisano 1202. Le due forme sono egualmente facili a scriversi, ma la prima è in tipografia molto più comoda della seconda; ed è anche più facile a leggersi.
am "a elevato m". Questa notazione si trova in Cartesio 1637, e sostituì notazioni antiche.
= "eguale", introdotto da Recorde nel 1557, usato da Newton (1660-1727), si è diffuso dappertutto, sostituendo l'iniziale della parola aequalis prima usata.
> " maggiore" e < "minore", si trovano in Harriot 1631, e sostituirono segni prima usati.
Se a e b sono interi, a/b, "a diviso b" è in generale un numero fratto.
Scriveremo "a quot b", ed "a resto b" per indicare il quoto o quoziente intero della divisione di a per b.
ESEMPIO:
50 quot 7 = 7
50 resto 7 = 1
Non c'è una notazione uniforme per indicare questi risultati; la più comune è quot (a, b) e resto (a, b). Anche il valore delle parole quoto e quoziente non è uniforme nei libri.
Per indicare l'ordine delle operazioni aritmetiche, si usarono varie notazioni; la più comune è quella delle parentesi, che fu diffusa specialmente da Eulero.
Per ulteriori informazioni storiche, vedasi il mio articolo: Sulla forma
dei segni di Algebra, "Giornale di Matematica finanziaria",
diretto dal prof. INSOLERA, Torino 1919.
Dovendosi fare più operazioni successive, p. es. 1+2+3+4. si dice 1 più 2,
eguale 3, più 3, eguale 6, più 4, eguale l0. In alcuni libri sta scritto:
1+ 2 = 3 + 3 = 6 + 4 = 10;
questa notazione è giudicata erronea dalla maggioranza. Ma la verità, anche in matematica, è relativa alle convenzioni che si fanno. Chi la giudica erronea, intende che essa significhi 1 + 2 = (3 + 3); mentre quelli che la usano, intendono che significhi ((1+ 2 = 3) + 3 = 6 ) + 4 = 10.
Le parentesi iniziali, in ogni formula matematica, sono inutili, come pure le chiuse finali. Quindi si può abbreviare la scrittura così:
1+ 2 = 3) + 3 = 6) +4 = 10.
Questa scrittura non si presta ad equivoci, e ha tutti i vantaggi della
brevità; ma ha l'inconveniente della novità.
Chi non adotta questa convenzione, deve scrivere:
1+ 2 = 3; 3 + 3 = 6; 6 + 4 = 10.
Se il numero che si scrive due volte è complicato, Eulero lo rappresenta con p, leggi "precedente":
1+ 2 = 3, p + 3 = 6, p+ 4 = 10.
Nelle frazioni decimali, per separare la parte intera dalla rimanente mantissa, da noi si suole usare la virgola 2,3 = 2 + 3/10. Ma essendovi pericolo di confondere questa virgola decimale colla virgola ortografica, gli autori inglesi specialmente, ed anche altri, usano il punto in alto. così 3.14 = 3 + 14/100. In alcune tavole di logaritmi si trova anche il punto in basso.
§1. In aritmetica elementare si dà per ogni operazione una regola.
Ma sonvi altri modi per eseguire le stesse operazioni, che alcune volte sono
più opportuni di quelli che si studiano in aritmetica pratica. Questi metodi
sono esposti negli antichi libri. Il grande matematico Cauchy se ne occupò in
più memorie all'Accademia delle Scienze di Parigi, nel 1840. Altri sono esposti
dal calcolatore Houzeau nell' Accademia delle Scienze di Bruxelles, a. 1875.
Sonvi anche libri speciali su questo soggetto. Vedasi: UGO CASSINA, Calcolo
numerico, Libreria Perotti, Torino, 1923.
Questo libro contiene preziose informazioni storiche sui calcoli elementari,
come pure sulle radici, logaritmi, sviluppi in serie, ecc.
§ 2. I calcolatori consigliano, dopo aver calcolato la somma delle cifre di una colonna, di scrivere la cifra del riporto nella colonna di sinistra in tal modo si può interrompere l'operazione, senza dover ricominciare da capo; e si può verificare una colonna, indipendentemente dalle altre. Ciò è specialmente utile, dovendosi sommare molti numeri.
Riporti |
1200 |
Stella di 1a grandezza |
20 |
Stella di 2a grandezza |
51 |
Stella di 3a grandezza |
200 |
Stella di 4a grandezza |
595 |
Stella di 5a grandezza |
1213 |
Stella di 6a grandezza |
3640 |
Somma |
5719 |
ESEMPIO: Conoscendo il numero delle stelle delle varie grandezze, dalla prima
o più luminosa fino alla sesta, che sono le più piccole, che si possano vedere
ad occhio nudo, per trovare il numero delle stelle visibili ad occhio nudo, si
fa la somma. La somma delle unità vale 9, che si scrive. La somma delle decine
vale 21; scrivo l nella somma, e scrivo 2 nei riporti, colonna delle centinaia.
La somma delle centinaia vale 17; scrivo 7 centinaia nella somma, e l migliaio
nei riporti.
Le stelle che si possono vedere ad occhio nudo, in un dato momento, sono solo la
metà delle precedenti, circa 3000, quanti gli abitanti di un piccolo villaggio.
§ 3. Cauchy insegna una prova dell'addizione. Si sommano le cifre
degli addendi:
2 + 6 + 2 + 19 + 7 + 13, con quelle dei riporti 3 = 52. Si sommano le cifre del
totale 22 con quelle dei riporti moltiplicati per l0, cioè 30; e si ha 52 come
prima.
§ 4. L'addizione si può fare da sinistra e destra. Nell'esercizio precedente, sommo prima le migliaia, poi le centinaia, poi le decine, poi le unità; e poi addiziono le somme parziali.
4000 1500 210 9 ______ 5719 |
§ 5. I contabili (così riferisce Houteau), per calcolare una lunga
somma, usano il metodo che qui espongo col breve esempio precedente.
Sommate le 9 unità, si passa alle decine, e si dice: 2 + 5 = 7; 7 + 9 = 16,
pongo il * che vuoI dire l0. e dico 6; 6 + l = 7, 7 + 4 = 11, pongo * che
significa l0, e scrivo l nella somma. Conto gli * segnati, e li riporto come
centinaia. 2 di riporto + 2 = 4; 4+5=9; 9+2= 1l, scrivo *, e dico l; l +6=7 che
scrivo nella somma e riporto un *.
2 0 5 1 2 0 0 5 9*5 1 2*1 3 3 6 4*0 ____________ 5 7 1 9 |
§ 6. Addizione col nastro (addition au ruban di HOUZEAU).
Nelle banche si usa una riga fissa, lunga un decimetro, su cui sono segnati i
centimetri, ed un nastro lungo circa un metro, su cui sono pure segnati i
centimetri; e si misurano successivamente sul nastro tanti centimetri quante
sono le unità delle cifre di una colonna, e si legge la somma sul nastro.
Invece della lunghezza del centimetro, è più comodo il pollice, che si può
fare di 2 centimetri.
Sonvi anche macchine addizionatrici, alcune abbastanza semplici, ma non
elementari.
§ 7. Addizione e Sottrazione contemporanee (o somma algebrica di
numeri).
La somma di più numeri relativi dicesi anche "somma algebrica".
Nell'uso comune avendosi da sommare dei numeri positivi e negativi, quali
"entrata e uscita", "attivo e passivo ", "debito e
credito", si suoI tenere due registri, l'uno delle entrate, o dei termini
positivi, e l'altro delle uscite, o dei termini negativi, sommarli
rispettivamente, e poi farne la differenza. Spesso si tiene un registro solo, ma
le entrate si scrivono m una colonna e le uscite in un'altra. Ciò però non è
necessario. vogliasi per es. calcolare la somma qui. scritta in cui i termini
sono alternativamente positivi e negativi (e ognuno è la parte intera del
precedente divisa per 2).
Sommo per colonne dall'alto in basso. Sommo le cifre delle unità. e dico:
0 - 0 = 0) + 0 = 0) - 5 = - 5) +2 = - 3) - 1 = - 4) + 5 = 1) - 7 = - 6) + 3 = -
3) - 1 = - 4 = 6 -10; scrivo 6 nella colonna delle unità, e riporto -1. Sommo
le decine e dico: - 1 di riporto + 5 = 4) - 2 = 2) + 6 = 8) - 3 = 5) + 1 = 6,
che scrivo. Sommo le centinaia: 10 - 5 = 5) + 2 = 7) - 1 = 6, che scrivo, ed ho
la somma 666.
-500 +250 -125 +62 -31 +15 -7 +3 -1 _________ 666 |
§ 8. I prodotti di due cifre una volta si facevano imparare a mente, facendoli ripetere più volte, con una cantilena, che già fu giudicata odiosa da S. Agostino, anno 354 al 450: "unum et unum duo, duo et duo quatuor, odiosa cantio mihi erat" (Confessiones I, 13). Egli attesta che in quei tempi nelle scuole si faceva anche odiare il greco ed il sommo Omero.
LUCAS, Arithmétique amusante. Paris 1895, dice:
"Pour apprendre à notre écolier la multiplication, gar- dons nous bien de
lui faire réciter, sur un ton dolent et monotone, deux fois deux font quatre.
deux fois trois font six,...; ce serait donner à ses facultés arithmétiques
un enterrement de première classe. L'enfant doit construire la Table lui-meme".
Lo stesso dice LAISANT, lnitiation mathématique, Paris 1915, pag. 6: " Attachez-vouz à intéresser, à amuser l'enfant, ne lui faites rien apprendre par coeur". Gli stessi principii sono insegnati da tutti i pedagogisti.
§ 9. Per costruire la tavola di moltiplicazione, si scrivono sulla prima linea i numeri
1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Poi contando per 2, si ha la seconda linea:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
Si verifica che questi numeri si ottengono anche addizionando i numeri della prima linea con essi stessi; ossia si riconosce la proprietà commutativa del X:
2 X 8 = 8 X 2
I multipli di 3 si ottengono contando per 3:
3, 6, 9, 12, 15, 18, 21, 24, 27, 30.
Oppure addizionando i numeri della linea 1con quelli della 2.
Per moltiplicare per 4, si raddoppia due volte.
Per moltiplicare per 5, si osserva che:
2 X 5 =10. 4 X 5 = 20. 6 X 5 = 30. 8 X 5 = 40.
Poi 7 X 5 = (6 + l) X 5 = 6 X 5 + 5 = 30 + 5 = 35. 9 X 5 = 8 X 5 + 5 = 45.
Siccome la tavola non si altera, scambiando le linee colle colonne, rimangono
i prodotti di 6, 7, 8, 9.
6 X 6 = 6 X 5 + 6 = 30 + 6 = 36.
7 X 6 = 7 X 3 X 2 = 21 X 2 = 42.
8 X 6 = 8 X 3 X 2 = 24 X 2 = 48
= 5 X 6 + 3 X 6 = 30 + 18 = 48
= 8 X 5 + 8 = 40 + 8 = 48.
9 X 6=9 X 3 X 2 = 27 X 2 =54.
7 X 7 = 7 X 5 + 7 X 2 = 35 + 14 = 49.
8 X 7 = 2 X (4 X 7) = 2 X 28 = 56
= 8 X (5 + 2) = 40 + 16 = 56.
8 X 8 = 8 X 5 + 8 X 3 = 40 +24 = 64.
9 X 8 = 9 X 4 X 2 = 36 X 2 = 72.
I prodotti per 9 si ottengono facilmente colle regole:
9 X 9 =9 X (10 -1) = 90 - 9 = 81.
8 X 9 = 8 X (10 -1) = 80 - 8 = 72.
7 X 9 = 7 X (10 -1) = 70 - 7 = 63.
6 X 9 = 6 X (10 -1)= 60 - 6 = 54.
I quadrati si possono anche ottenere colla formula:
a2 = (a - 1) X (a + 1) + 1.
ESEMPIO: 52 = 4 X 6 + 1= 24 + 1= 25.
72 = 6 X 8 + 1= 48 + 1= 49.
In tal modo, un prodotto, che non ricordiamo, viene collegato ad altri più
facili.
§ 10. Per calcolare il prodotto di due cifre fra 5 e10, si può usare la
moltiplicazione digitale.
Per avere (5 + a) X (5 + b), ove a e b valgono da 1 a 4 si
dirizzino a dita della mano destra, e b della sinistra, e ad
(a + b) X 10 si aggiunga il prodotto delle dita rimaste piegate nelle due mani.
Infatti.
(5 + a)X(5+ b)= (a + b)X 10+ (5-a)X(5-b).
Questo metodo era noto agli Arabi, e forse ai Greci e Romani.
In altri tempi la stessa regola, col nome di moltiplicazione per
differenze, fu esposta così:
Per avere 9 X 8, scrivo accanto a questi due numeri le loro differenze a 10,
cioè 1e 2. Sommo i numeri della prima colonna e tolgo10; ho 7; moltiplico le
differenze 1X 2 = 2; il prodotto = 72.
9 1
8 2
____
7 2
§ 11. Moltiplicazione egiziana. Il papiro egizio del calcolatore
Ahmes, che rimonta ad oltre 4000 anni, contiene la seguente moltiplicazione di
35 per 42:
Nella prima colonna si scrive il fattore 35, si pone un segno + perché è
dispari; sottratto 1, si divide per 2, e si scrive sotto 17. Accanto a questo si
pone il segno + perché è dispari, e sottratto 1, si divide 16 per 2, e si ha
8, che si scrive sotto. Accanto a questo che è pari, non si pone alcun segno, e
si divide per 2, si ha 4 che si scrive sotto; poi sotto la sua metà 2, e sotto
la sua metà 1, accanto a cui si pone il segno + perché dispari. Nella seconda
colonna, sotto il 42, scrivo il doppio 84, poi, il suo doppio 168, poi il suo
doppio 336, poi 672, e infine 1344. Sommo i numeri della seconda colonna, che
sono accompagnati dal segno +, ed ho il prodotto cercato 1470.
Così la moltiplicazione è ridotta ad una serie di duplicazioni.
| 35+ 17+ 8 4 2 1+ |
42 84 168 336 672 1344 _______ 1470 |
Questa regola, ritrovata da molti autori più prossimi a noi, è ora una curiosità. Si giustifica osservando che nella colonna di sinistra si è decomposto il 35 in una somma di potenze di 2:
35 = 1 + 2 + 32,
e nella colonna di destra i termini col segno + sono precisamente:
1 X 42 = 42
2 X 42= 84
32 X 42 = 1344
la cui somma è il prodotto cercato.
§ 12. Regoli di Nepero. Su delle liste di carta o di legno si scrivono
le colonne della tavola di moltiplicazione. Le caselle quadrate sono divise con
una diagonale; in una parte si scrive la cifra delle decine, nell'altra quella
delle unità. Così nella figura, nella colonna 6 si leggono i multipli 12, 18,
24.

Poste vicine alcune di queste colonne, per es. quelle intestate 6, 3,7, si
leggono i prodotti di 637 per 2; da destra a sinistra: 4 unità, 1+6 =7 decine,
2 centinaia, 1 migliaio, cioè 1274.
Prodotto per 3: 1 unità, 2 + 9 = 11 decine; scrivo 1, e riporto 1, più 8 = 9
cento, 1 mille, cioè 1911.
Con un po' di attenzione si leggono i prodotti da sinistra a destra: 637 X X 4=
2548; per 5 = 3185; per 6 = 3822, ecc.
Questi regoli, che chiunque si può fabbricare, .sono molto utili nei lunghi
calcoli. Per moltiplicare due numeri di più cifre, coi regoli si moltiplica il
moltiplicando per le successive cifre del moltiplicatore, e si sommano i
prodotti parziali.
Nepero, inventore dei logaritmi, suggerì questo metodo in un libro Rhabdologia
del 1617.
Sonvi pure regoli, in cui si legge il prodotto di un nu- mero di più cifre per
una cifra, senza fare le addizioni. Vedasi la mia Aritmetica, ed.
Paravia, a. 1902, pag. 20.
§ 13. Moltiplicazione fulminea. I matematici Indiani, verso il 600,
eseguivano il prodotto di due numeri, anche senza passare per i nostri prodotti
parziali; e chiamarono questo procedimento "vajràbhyàsa", da "vajra"
= fulmine, e "abhyàsa"= moltiplicazione.
Essa è spiegata da Leonardo e posteriori.

Prendo il primo esempio in Leonardo: 37 X 49. Moltiplico unità per unità: 7 X 9 = 63. Scrivo 3 unità, e riporto 6 decine. Moltiplico unità per decine: 7 X 4 = 28 (decine), cui aggiungo 6 di riporto, 34; poi decine per unità 3 X9 = 27, più 34 = 61. Scrivo 1 decina e riporto 6 centinaia. Infine decine per decine 3 X 4 =12, + 6 di riporto, = 18, che scrivo, ed ho il prodotto 1.813.
Si può procedere da sinistra a destra; se i fattori hanno molte cifre, Fourier nel 1831, Cauchy nel 1840, e altri, consigliano di scrivere il moltiplicatore sopra una striscia di carta che, capovolta, si dispone successivamente sotto il moltiplicando nel modo indicato dalla figura. Allora si moltiplicano le cifre che stanno sulla stessa verticale e se ne fa la somma. Poi si sommano questi prodotti parziali nel modo indicato dalla figura.
§ 14. I calcoli sono facilitati da tavole numeriche. La più semplice è la tavola di moltiplicazione di due cifre. Essa dal 1600 è comunemente nota col nome di "tavola pitagorica ", mentre che prima questo nome indicava l'abaco.
Sonvi tavole dei prodotti di due numeri fino a 100, e formano un libretto. I prodotti di due numeri di tre cifre riempiono un volume. Non esistono tavole più ampie, e non sarebbero pratiche.
I manuali degli ingegneri sogliono contenere nelle prime pagine le tavole dei quadrati, dei cubi, delle radici, ecc. dei numeri fino a 1000, e sono molto utili.
L'Unione Tipografico-Editrice di Torino, pubblicò tavole siffatte in fascicolo separato, che sono molto comode anche per le scuole.
§ 15. Il prodotto di due numeri si può esprimere come differenza di due quadrati, colla formula:
a X b = [(a + b)/2]2 - [(a - b)/2]2,
che già trovasi in Euclide, libro Il prop. 5.
Avendosi, ad esempio, la tavola dei quadrati dei numeri da 1a 1000, si potrà ricavare il prodotto di due numeri di tre cifre, come risulta dagli esempi che seguono.
ESEMPIO 1°. Calcolare a X b, ove a = 981 e b = 223 sono dispari,
| a + b = 1204, | (a + b)/2 = 602, (questo)2 = | 36240 |
| a = 981 | ||
| b = 223 | ||
| a - b = 758, | (a - b)/2 = 379, (questo)2 = | 143641 |
| a X b = | 218763 |
La somma e differenza di a e b si fanno come d'ordinario, come pure la loro divisione per 2 i quadrati si leggono nella tavola.
ESEMPIO 2°. Se i due numeri sono pari, si può procedere come prima, oppure si possono dividere per 2:
| (a + b)/2 = 650 | , (questo)2 = 422500 | |
| a = 986, | a/2 = 493 | |
| b = 314, | b/2 = 157 | |
| (a - b)/2 = 336 | , (questo)2 = 112896 | |
| a X b = 309604 |
ESEMPIO 3°. Se i numeri sono l'uno pari e l'altro dispari, come 987 X 314, calcolo come prima:
| 986 X 314 = 30.0004 | |
| Aggiungo: | 314 |
| Trovo: | 987 X 314 = 309918 |
§ 16. -La tavola dei quadrati dei numeri da 1 a 1000 permette di calcolare rapidamente anche il quadrato di un numero di sei cifre. Se x e y sono numeri di tre cifre si ha: (1000 x + y)2 = x2 1000000 + [x2 + y2 -(x-y)2] 1000 + y2.
ESEMPIO: Vogliasi 3141592.
| 3142 = | 98 596 | ||
| 98 |
596 |
||
| 1592 = | 25 | 281 | |
| 25 | 281 | ||
| -1552 = | -24 |
025 |
|
| 3141592 = | 98 695 | 877 | 281 |
Quindi: 3,141592 = 9,8695877281.
Il numero che si eleva a quadrato è il valore di pi (greco) con 5 decimali. Non
bisogna credere che le 10 cifre trovate siano quelle di pi2
p2 = 9,869 604 4010...
§ 17. -Se il divisore ha più cifre, conviene calcolarsi la tavola dei suoi prodotti per 2, 3, 4, .., 9; o meglio leggerli nei regoli di Nepero. In ogni caso conviene scrivere i prodotti del divisore per le cifre del quoto, prima di fare la sottrazione. I calcolatori unanimi sconsigliano di fare la moltiplicazione e la sottrazione contemporanee.
§ 18. -Se il dividendo è multiplo del divisore, si può calcolare il quoto anche da destra a sinistra.
Se il divisore termina con cifra pari o con 5 cioè è multiplo di 2 o di 5, lo stesso avverrà del dividendo, e possiamo semplificare per questo fattore comune; allora il divisore terminerà con una cifra dispari diversa da 5.
Sia da dividere 309918 per 987. La cifra delle unità del quoto sarà 4, perché 7 X 4 = 28, termina per 8.
Dal dividendo sottraggo il divisore moltiplicato per 4; poi determino la cifra delle decine e quella delle centinaia, come qui accanto, e trovo per quoto 314, ossia verifico la moltiplicazione del § 15
| 309918 | |
| 4X987 = | 3948 |
| Differenza = | 30597 |
| 10X987= | 987 |
| Differenza = | 2961 |
| 300X987 = | 2961 |
| Differenza = | 0 |
Le questioni sul calendario, quale il giorno della settimana corrispondente ad una data, l'età della luna, il giorno di Pasqua, costituiscono utili ed interessanti esercizii di aritmetica elementare.
§ 1. Gli anni si sogliono indicare con numeri progressivi, a partire
da qualche avvenimento importante.
I Greci li numeravano dalle Olimpiadi; i Romani dalla fondazione di Roma.
Il monaco Dionysio Exiguo, o Dionigi il piccolo, nel 527, propose di contare gli
anni dalla nascita di Cristo; questo uso si diffuse, e divenne generale in
Europa verso il 1000. Si ha:
Anno cristiano a = anno di Roma (753 + a) = anno delle Olimpiadi (776 + a).
ESEMPIO 1° L'anno cristiano 1924 è l'anno di Roma 2677, ed è l'anno 2700 dell'Olimpiadi.
ESEMPIO 2° Censorino pubblicò il "de die natali liber" che spiega
il calendario ai suoi tempi. Egli dice: "Hic annus ab Olimpiade prima
millensimus est et quartus decimus. A Roma autem condita nongentensimus
nonagesimus primus"; cioè l'anno in cui scriveva era il 1014 delle
Olimpiadi, e l'anno di Roma 991. In quale anno egli scrisse quella pagina?
(R. L'anno cristiano 238).
§ 2. Nell'uso comune, il numero a dell'anno è positivo. Gli
astronomi attribuiscono ad a anche il valore 0 e valori negativi. Quindi l'anno
1 è preceduto dall'anno 0, e questo dall'anno -1, e cosi via.
Quindi:
anno 1900 = anno 0 + 1900 anni;
anno -43 = anno 0 - 43 anni;
anno 1900 - anno - 43 = 1943 anni;
anno -753 = anno di Roma 0;
anno -752 = anno di Roma 1.
Gli storici invece dicono "anno 1 avanti Cristo" l'anno, precedente
l'anno 1 dopo C., cioè l'anno 0 degli astronomi.
L'anno 1 di Roma è l'anno 753 a. C. Però altri storici dicono anno avanti C.
l'anno -a ed altri usano ora l'una, ora l'altra convenzione.
§ 3. La parola mese una volta significava luna.
Questa parola viene dal latino mense (accusativo mense-m); la
lettera n si conserva nell'italiano mensile. Quella parola ha
la radice men, che troviamo nelle parole derivate dal greco: men-isco
= piccola luna, neo-men-ia = nuova luna. La stessa radice si trova
nell'inglese moon, tedesco Mond = luna, come pure in russo e
in sanscrito.
Romulo che, si dice, fu col fratello Remo allattato da una, lupa, fondò Roma il
21 aprile dell'anno primo di Roma, cioè l'anno 753 a. C. Tale tradizione,
fissata da Varrone, che scrisse l'anno 43 a. C., è ora seguita da tutti.
Romulo formò un calendario di dieci mesi, martius, dedicato a Marte,
dio dell'agricoltura, poi della guerra; aprilis, maius, iunius;
segue quintilis, che fu detto iulius in onore di Giulio
Cesare, anno 44 a. C. ; sextilis detto augustus in onore di
Cesare Augusto, l'anno 8 a. C.; vengono poi september, october,
november, december, i cui nomi indicano il posto nel
calendario romuleo.
Numa, secondo re di Roma, aggiunse i mesi di ianuarius, dedicato a
Giano, e februarius, dedicato ai morti e agli Dei inferi: e ciò sotto
l'influenza di Pitagora: Così dice OVIDIO, Fasti, III.
I mesi avevano un numero dispari di giorni, cioè 31 i mesi di marzo, maggio,
luglio, ottobre, e 29 gli altri; secondo il precetto, ricordato da Virgilio:
"numero deus impari gaudet" (che uno studente tradusse: il numero due
gode di essere impari). Unica eccezione il febbraio, dedicato agli dei
infernali, che aveva 28 giorni.
Risulta che il calendario di Numa aveva 355 giorni = 12 lunazioni + frazione di
giorno.
I mesi seguivano il corso della luna. Una intercalazione faceva concordare il
calendario lunare col corso delle stagioni, o anno.
Il primo giorno del mese, o luna nuova, dicevasi calendas, onde la
parola calendario.
Giulio Cesare, dittatore e pontefice massimo, attribuì ai mesi il numero di
giorni che ancora conservano, cioè 30 ad aprile, giugno, settembre, novembre, e
31 a tutti gli altri, eccettuato febbraio, cui ne conservò 28, "ne deum
inferum religio immutaretur" (MACROBIO, Saturn., I, 14). E ordinò
che ogni quarto anno si intercalasse il giorno bissexto avanti al
giorno sesto avanti le calende di marzo, giorno anniversario del "regifugium",
o cacciata dei re, e proclamazione della republica. L'anno col giorno
intercalare si dice bisestile; gli altri anni sono comuni.
Questo calendario, detto giuliano, ebbe principio al novilunio seguente
il solstizio d'inverno, il primo gennaio dell'anno 45 a. C. cioè l'anno -44
degli astronomi.
Così, per ordine di Cesare, i mesi cessarono di seguire la luna.
L'equinozio di primavera, ai tempi di Cesare, fu fissato al 25 marzo. Il
Concilio di Nicea, che ebbe luogo l'anno 325, nel fissare la data della Pasqua,
assunse il 21 marzo come giorno dell'equinozio. Verso l'anno 1500, l'equinozio
vero cadeva circa l'11 marzo. Il pontefice Gregorio XIII volle ristabilire
l'equinozio ai tempi del concilio di Nicea. Quindi ordinò che il giorno
seguente il "4 ottobre 1582 giovedì" fosse chiamato " 15 ottobre
1582 venerdì", e che in futuro gli anni multipli di 100 e non di 400,
fossero comuni.
E ciò per ragioni ecclesiastiche "rebus ecclesiasticis maxime ", e
cioè per impedire che dopo 23000 anni il Natale venisse a cadere d'estate, e S.
Giovanni d'inverno, ciò che avviene nei paesi situati nell'altro emisfero, come
la Repubblica Argentina.
Il calendario gregoriano sostituì il giuliano dapprima presso i popoli
cattolici, poi presso gli altri; fu adottato in Russia dal 10 gennaio 1918 e in
Grecia dal 10 marzo 1923. Così l'unità del calendario, rotta da Gregorio, si
è ricostituita presso i popoli europei.
I nomi dei mesi sono gli stessi, salvo l'ortografia, in tutte le lingue europee.
§ 4. L'anno giuliano a è bisestile, se a è
multiplo di 4; ossia se le due ultime cifre a destra formano un numero multiplo
di 4; ossia se la cifra delle unità è pari, e la sua metà sommata colla cifra
delle decine dà un numero pari.
L'anno gregoriano a segue la stessa regola pei bisestili, eccettuato il
caso in cui a è multiplo di 100, e non di 400. L'anno 1900 è comune;
il 1924 bisestile, il 1925 comune, il 1926 comune.
§ 5. Per ricordare quali mesi hanno 30 e 31 giorni, sonvi regole
mnemoniche in versi. Oppure si può adottare la regola seguente:
Segnati quattro + intercalati da tre -, si pongono sotto 1 essi ordinatamente i
mesi, e ricominciando da capo quando la 1 linea è finita. I mesi che
corrispondono al + hanno 31 giorni; quelli che corrispondono al - hanno 30
giorni, febbraio eccettuato:>
| + | - | + | - | + | - | + |
| G | F | Mar | Ap | Mag | G | L |
| Ag | S | O | N | D |
I + si possono far corrispondere alle nocche delle 4 dita del pugno, e i -
alle 3 cavità fra due dita.
Detto m il numero del mese, cioè gennaio1, febbraio 2,... dicembre 12,
allora il mese m ha giorni
31 - (m -1) resto 7 resto 2,
per m =1, 3, 4,....., 12. E' la regola precedente.
Oppure si segnino tre + intercalati da due - e si cominci a contare da marzo; i
mesi corrispondenti al + hanno 31 giorni:>
| + | - | + | - | + |
| M | A | M | G | L |
| A | S | O | N | D |
| G |
I + si possono rappresentare col pollice, medio e mignolo alzati; i - coll'indice
e anulare piegati.
Se m è il numero del mese, allora il mese ha giorni
31 - (m - 3) resto 5 resto 2,
per m = 3, 4, ..... 12.
§ 6 . Per trovare la differenza. fra due date appartenenti allo
stesso anno, i commercianti, nel calcolo degli interessi, indicano i giorni
dell' anno con numeri progressivi, che sono segnati in molti calendarii. Così
si liberano dai mesi t diseguali, e che non seguono la luna.
Lo stesso fanno gli astronomi. Questi chiamano giorno 0 di un anno comune il
giorno che precede il 10 gennaio, cioè l'ultimo giorno dell'anno precedente.
Per esprimere il giorno g del mese m in giorno dell'anno,
basta sommare g col numero dei giorni che nell'anno precedono il mese m
.
Il numero dei giorni che nell'anno comune precedono gennaio è 0, febbraio 31,
marzo 59, aprile 90, maggio 120, giugno 151, luglio 181, agosto 212, settembre
243, ottobre 273, novembre 304, decembre(1) 334.
(Nota 1) In italiano si scrive dicembre e decembre. La prima forma è più popolare la seconda è latina, e più internazionale, francese décembre, inglese e tedesco december, portoghese dezembro, e cosi in russo e greco moderno. Lo spagnuolo ha le due forme diciembre e deciembre. Parimenti l'italiano, scrivendo accademia per academia, repubblica per republica, si allontana dal latino più che ogni altra lingua.
Dando ai mesi i numeri marzo 3, aprile 4, maggio 5, ........ dicembre 12, allora il numero dei giorni che precedono il mese m >= 3 vale:
(m -1) X 30 + (3m - 2) quot 5 - 2.
ESEMPIO: Di quanti giorni l'equinozio di autunno, 21 settembre, segue quello
di primavera, 21 marzo?
21 marzo = giorno 0 dell'anno + (giorni precedenti marzo = 59) + 21 d. = giorno
0+ 80 d.
21 settembre = giorno 0+ 264 d.
21 settembre -21 marzo = 184 d.
(d significa giorno, latino dies ).
Come esercizio numerico, si possono risolvere queste questioni:
Il giorno 100 dell'anno comune è il 10 aprile.
Il giorno 200 è il 19 luglio.
Il giorno 300 è il 27 ottobre.
Il giorno medio dell'anno è il 2 luglio.
Secondo la legge italiana, 4 agosto 1913, sono festivi, oltre le domeniche e
l'Ascensione, i giorni:
Capo d'anno, 1° gennaio; Epifania, 6 gennaio; Assunzione, 15 agosto; il Venti
Settembre; Ognissanti, 1 novembre; e Natale, 25 decembre. Questi giorni,
nell'anno comune, hanno i numeri 1, 6, 227, 263, 305, 359.
§ 7. Negli anni bisestili, gli astronomi chiamano giorno 0 dell'anno
il primo gennaio.
Il giorno g del mese m dell'anno bisestile = giorno 0
dell'anno + numero dei giorni che nell'anno comune precedono li il mese m,
come in § 6; eccetto pei mesi di gennaio e febbraio, in cui la data 9
deve essere diminuita di 1.
Così i giorni sono computati da 0 a 365. I commercianti sogliono numerarli da 1
a 366.
§ 8. Per trovare la differenza fra due date nel corrente secolo, conviene riferirci all'anno 1900 giorno 0. Se n vale 1, 2, ..., 199, si ha:
Anno (1900 + n) d 0 = anno 1900 d 0 + (365 X n + n quot 4) d.
365 X n è il numero dei giorni in n anni comuni; n quot 4 è il numero dei giorni bisestili, tenendo conto della convenzione § 7 .
ESEMPIO: Il giorno 10 agosto 1914, il Kaiser di Germania i dichiarò la
guerra allo Csar di Russia, producendo la guerra mondiale, che ebbe termine
all'11 novembre 1918. Quanti
giorni durò la guerra?
11 novembre 1918 = anno 1900 d 0+ (365 X 18 + 18 quot 4 + 304 + 11) d
1 agosto 1914 = anno 1900 d 0+(365 X 14 + 14 quot 4+ 212 + 1)d
11 novembre 1918-1° agosto 1914 = (365 X 4 + 1 + 92 + 10) d.
La guerra durò 1563 giorni.
§ 9. Per trovare la differenza in giorni fra due date, di cui una almeno dei secoli passati, ci riferiamo all'anno 0 d 0, colle formule:
Anno giuliano a d 0 =
= anno 0 d 0 + (365 X a + a quot 4) d
Anno gregoriano a d 0 =
= anno (giuliano) 0 d 0+ (365 X a + a quot 4 -a quot
100 + a quot 400 + 2) d.
ESEMPIO. Anno -44 d 0 =anno 0 d 0 -16071 d.
Anno 1900 d 0 = anno 0 d 0 + 693962 d.
Anno 1900 d 0 -Anno -44 d 0 = 710033 d.
Vedi § 31, es. 2.
§ 10. La settimana è un periodo di sette giorni, circa un quarto di
luna. Essi sono dedicati ai pianeti Sole, Luna, Marte, Mercurio, Giove, Venere e
Saturno.
La settimana è di origine orientale. La Bibbia ne parla, nella prima pagina,
senza i nomi dei pianeti. Questi erano noti agli antichi Babilonesi. Una
iscrizione, parlando di Nabucodonosor, re di Babilonia verso l'anno 600 a. C.,
dice: "Egli ha elevato un tempio alle sette sfere del Cielo".
La settimana venne in uso in Europa sotto l'impero Romano. La più antica
iscrizione contenente i nomi dei giorni della settimana, fu scoperta a Pompei,
che fu sepolta l'anno 79 dopo Cristo.
Il giorno di Saturno si dice sabbato dall'ebraico.
Il giorno del Sole fu detto dominica ai tempi dell'imperatore
Costantino, anno 337. In inglese sunday, tedesco Sonntag =
giorno del Sole.
La settimana è usata dai cristiani, israeliti e mussulmani; il giorno di riposo
è la domenica presso i cristiani, il sabato presso gli israeliti e il venerdì
presso i maomettani; sicchè nelle città a popolazione mista dell'Africa
settentrionale, la settimana ha tre giorni festivi.
La settimana non fu mai interrotta, nei tempi storici, nemmeno dalla riforma
gregoriana.
§ 11. Definiamo S, leggi "settimanale", in questo modo:
S domenica = 0. S lunedì = 1. S martedì = 2.... S sabato = 6.
ESEMPIO: S. Pasqua = 0, leggi "Pasqua è di domenica". S (anno 1900 d
0) = 0, leggi "il giorno precedente il 1° gennaio 1900 fu domenica ".
.
Con questa convenzione, ai giorni della settimana sostituiamo i numeri 0, 1, 2,
6.
§ 12. Conoscendo il settimanale di un giorno g, si trova il
settimanale del giorno che lo segue di x giorni, colla formula:
S (giorno g + x d) = (S giorno g + x) resto
7.
ESEMPIO: S. Pentecoste = S (Pasqua + 49 d) = (0 + 49) resto 7 = 0;
ossia Pentecoste è di domenica.
S (Ceneri) = S (Pasqua -46 d) = (0-46) resto 7 = = (-7 X 7 + 3) resto 7 = 3;
le Ceneri sono di mercoledì.
In questo esempio, il numero x è negativo. Con questa regola, e con
quelle dei §§ 6-9, possiamo trovare il settimanale corrispondente a
qualunque data. Ma le formule si possono semplificare.
§ 13. Il Settimanale di un anno è il settimanale del giorno 0
dell'anno, definito in § 6 e § 7.
Per il corrente secolo, se n è uno dei numeri 0, 1,2, ....... 99, si
ha:
S anno (1900 + n ) = (n + n quot 4) resto 7.
Risulta dal § 8 e § 12 .
ESEMPIO: S (anno 1924) = 2, S (anno 1925) = 3, ecc.. Cioè l'anno bisestile 1924 comincia di martedì; il 1° gennaio 1925 ha per settimanale 3 + 1 = 4, cioè è giovedì.
§ 14. Nel calendario giuliano:
S anno a = (4+a +a quot 4) resto 7.
§ 15. Nel calendario gregoriano conviene ridurre l'anno alla forma 100 s + n, ove s indica il secolo, ed n è un numero da 0 a 99. Si ha:
S anno 100 s = 6 -2 (s resto 4).
S anno (100 s + n ) = (S anno 100 s + n + n quot 4) resto 7.
Risulta
S anno 1500 = 0.
S anno 1600 = 6.
S anno 1700 = 4.
S anno 1800 = 2.
Sanno 1900 = 0.
S anno 2000 = 6.
§16. Settimanale d'un mese è il resto per 7 del numero dei giorni
che nell'anno comune precedono il mese.
Dividendo per 7 i numeri del § 6, si ha:
S gennaio = 0.
S febbraio = 3.
S marzo = 3.
S aprile = 6.
S maggio = 1.
S giugno = 4.
S luglio = 6.
S agosto = 2.
S settembre = 5.
S ottobre = 0.
S novembre = 3.
S decembre = 5.
Volendo risolvere a memoria il problema di trovare il giorno della settimana
corrispondente ad una data, bisogna ricordare la tabella precedente.
Un metodo mnemonico è di ricordare la frase:
Civi aurato aureum linum.
L'assenza di vocale iniziale significa 0; le vocali a, e, i, o, u
valgono 1, 2, 3, 4, 5; e au vale 1 + 5 = 6. Quindi in quella frase
leggiamo la successione di numeri:
0, 3, 3; 6, 1, 4; 6, 2, 5;0, 3, 5. Per attribuire un senso a quella frase,
teniamo presente che "eques auratus" fu un titolo onorifico, che ebbe
Newton.
Quindi possiamo tradurre "al cittadino cavaliere diamo una veste intessuta
d'oro".
OZANAM, Recréations mathématiques, 1693, cita i versi latini:
Astra Dabit Dominus, Gratisque Beabit Egenos,
Grata Cristicolae, Feret Aurea Dona Fideli.
ove le lettere iniziali A = 0, B = 1, C = 2, D = 3, E = 4, F=5, G=6.
E i versi francesi:
Au Dieu De Gioire Bien Espere
Grand Coeur, Faveur Aime De Faire.
Oppure, ricordiamo che il settimanale di gennaio è 0, di febbraio 3.
Se m vale 3, 4, ...,12
S mese m = [2 (m + 1) + [3 (m + 1)] quot 5] resto 7.
Questa è una trasformazione della formula del § 6 .
§ 17. Così determinato il settimanale di un mese qualunque m,
e di un anno qualunque a, si ha:
S (giorno g del mese m delI'anno comune a)
= (g + S mese m + S anno a) resto 7.
Per gli anni bisestili si applica la stessa formula, eccettuati i mesi di
gennaio e febbraio, in cui la data si deve diminuire di 1.
ESEMPIO: Trovare il giorno della settimana, corrispondente all'11 novembre
1918.
Scrivo in corrispondenza 11 + 3 + 0 + 18 + 4, cioè ripeto 11, giorno del mese;
sotto novembre scrivo il settimanale 3, secondo la regola § 16 ; sotto
il 1900 scrivo il suo settimanale 0, secondo la regola § 15 ; poi scrivo
18, che indica l'anno nel secolo, e il suo quarto 4, secondo la regola § 13
; sommo e tolgo i multipli di 7, secondo la regola §17 . Ottengo per
settimanale1, cioè la guerra europea terminò di lunedì.
ESEMPIO di calendario giuliano: Il 16 luglio anno 622, Maometto fuggi dalla
Mecca. Dalla regola § 14 :
Settimanale anno 622 =(4 + 622 + 622 quoto 4) resto 7 = 4.
S (16 luglio 622) = (16 + 6 + 4) resto 7 = 5.
Quel giorno era venerdì, ed i Maomettani fanno festivo il giorno di Venere.
§ 18. Settimanali importanti.
Cristoforo Colombo sbarca in America il 12 ottobre 1492, venerdì.
Presa della Bastiglia a Parigi, 14 luglio 1789, martedì. Il suo anniversario è
festa nazionale francese.
Gioacchino Rossini; celebre musico, nacque il 29 febbraio 1792, mercoledì. Si
badi all'anno bisestile.
Garibaldi entra vittorioso in Palermo il 27 maggio 1860, domenica.
Dichiarazione di guerra del Kaiser di Germania allo Csar di Russia, il 1°
agosto 1914, sabato.
L'esercizio aritmetico diventa più interessante, se si determina il
settimanale del giorno in cui sono nati gli allievi, e se ne trae l'oroscopo: i
nati di lunedì sono poeti e artisti; di martedì nascono gli eroi e le eroine;
di mercoledì i mercanti, industriali e ingegneri; chi nasce nel giorno di Giove
sarà sempre gioviale; Venere dà ai nati sotto il suo segno le grazie e tutte
le fortune; Saturno rende saggi e dotti i suoi favoriti; chi nasce di domenica
sarà potente e glorioso.
Tutti gli artifizi sono buoni, se rendono meno noiosa l'aritmetica.
Il problema del giorno della settimana corrispondente ad una data, si risolve
pure con tavolette, ma allora cessa l'applicazione aritmetica, la quale risolve
il problema, senza tavole, purché si ricordino le regole.
Tavole semplicissime furono pubblicate nel Calendario Perpetuo del col.
Satta, nel periodico Urania, diretta dal prof. Sacco, in Torino, anno
1922.
§ 19. Il problema di determinare quanti giorni ha la luna in una
determinata notte, se sia nuova o piena, fu risolto dagli antichi coll'epatta.
Questo calcolo nei secoli scorsi faceva parte della matematica elementare; ora
è completamente escluso dalle nostre scuole, mentre costituisce un utile
esercizio di aritmetica.
Epatta, latino epacta, dal greco, significa addendo.
Epatta di un anno è il numero dei giorni che ha la luna, il giorno zero
dell'anno. Questo numero sta scritto in tutti i calendarii. Da esso dipende la
Pasqua, colle altre feste mobili.
§ 20. Siccome il mese lunare ha da 29 a 30 giorni, e il mese civile
ne ha 30 o 31, febbraio escluso, ne viene che l'età della luna in un giorno di
un mese vaIe l'età nello stesso giorno del mese precedente, più uno.
Porremo pertanto, abbreviando epatta in E:
| Mese | E |
| Gennaio | 0 |
| Febbraio | 1 |
| Marzo | 0 |
| Aprile | 1 |
| Maggio | 2 |
| Giugno | 3 |
| Luglio | 4 |
| Agosto | 5 |
| Settembre | 6 |
| Ottobre | 7 |
| Novembre | 8 |
| Dicembre | 9 |
Allora:
Età della luna il giorno g del mese m dell'anno a
=
= (g + E mese m + E anno a) resto 30.
La luna è nuova se la sua età =0; si ritiene piena, se ha 14 giorni.
La differenza fra l'età. della luna così calcolata, e quella calcolata dagli
astronomi, può raggiungere 1, e, in rari casi, 2 giorni; il che non ha
importanza nella vita civile.
ESEMPIO: L'età della luna il 25 dicembre 1924 = (25 + 9 + 24) resto 30 = 28, prossimo al novilunio; la notte di Natale di quest'anno non è illuminata dalla luna.
§ 21. L'epatta dell'anno 1900 + n, ove n è un numero da 0 a 299, = [29 + (n resto 19) X 11] resto 30.
ESEMPIO:
| Anno | Epatta anno |
| 1900 | 29 |
| 1901 | 10 |
| 1902 | 21 |
| 1903 | 2 |
| 1904 | 13 |
| 1905 | 24 |
| ... | ... |
| 1924 | 24 |
| 1925 | 5 |
| 1926 | 16 |
| ... | |
Se all'epatta di un anno aggiungo 11, e se la somma vale 30 o più, sottraggo
30, ottengo l'epatta dell'anno seguente; però se il numero dell'anno è
multiplo di 19, la sua epatta supera la precedente di 12.
Le epatte si riproducono ogni 19 anni, nei limiti di tempo indicati.
Questa regola per determinare l'età della luna fu annunziata da Metone ateniese
nei giochi olimpici dell'anno 432 a. C. I Cinesi la attribuiscono all'imperatore
Hoang-Ti dell'anno 2638
av. Cristo.
§ 22. Il concilio cristiano, tenutosi a Nicea, città dell'Asia
presso Costantinopoli nell'anno 325, fissò la regola:
Epatta anno giuliano a = [8 + (a resto 19) X 11] resto 30,
che è sempre la regola di Metone, con origine differente.
ESEMPIO: Carlo Magno fu coronato imperatore la notte di Natale dell'anno 800. Qual giorno della settimana, e quanti giorni aveva la luna?
S anno 800 = (4 + 800 + 200) resto 7 = 3
S (25 decembre 800) = (25 + 5 + 3) resto 7 = 5, venerdì.
Epatta anno 800 = [8 + (800 resto 19) X 11] resto 30.
= (8 + 2 X 11) resto 30
= (8 + 22) resto 30 = 0.
Età luna 25 decembre 800 = (25 + 9 + 0) resto 30 = 4.
Il Natale dell'800 era di venerdì, e la luna aveva 4 giorni.
§ 23. L' età della luna vera supera quella data da Metone di un giorno circa ogni 300 anni giuliani; verso il 1500 la differenza era di 3 giorni.
ESEMPIO: La notte di San Bartolomeo, precedente il 24 agosto 1572, d'ordine
del re Carlo IX, furono uccisi a tradimento i protestanti di Francia. Quella
notte fu illuminata dalla luna?
RISPOSTA: E anno 1572 = [8 + (1572 resto 19) X 11] resto 30 = 12.
E (24 agosto 1572) = (24 + 5 + 12) resto 30 = 11.
Aggiungendo l'errore di 3 giorni, si ha che la luna aveva 14 giorni, cioè era
piena. Il calcolo astronomico dice che la luna piena avvenne il 23 agosto ore10.
§ 24. Il papa Gregorio XIII, colla sua riforma del 1582, oltre a far
avanzare il sole di 10 giorni, fece pure scorrere la luna avanti di 3 giorni; e
affinché la differenza nel futuro fosse minima, aggiunse all'epatta un giorno
ogni 300 anni giuliani, fino all'anno 4199.
Traducendo gli anni giuliani in gregoriani, si ha la formula:
Epatta anno gregoriano a =
= [8 + (a resto 19) X 11- a quot 100 + a quot 400 + a
quot 300] resto 30.
I due primi termini coincidono colla formula di Metone § 21 ; gli
altri due termini trasformano gli anni gregoriani in giuljani; l'ultimo termine
a quot 300 è la correzione introdotta da Gregorio.
Se il calendario dovesse rimanere immutato oltre l'anno 4199, allora invece del
termine a quot 300 si userà il termine
[8 (a quot 100) + 13] quot 25
§ 25. ESEMPIO 1. Garibaldi, dopo la ritirata da Roma, il giorno 1°
agosto 1849 si imbarca a Cesenatico, per recarsi a Venezia. Ma al chiarore della
luna è visto dalle navi austriache, e costretto a prender terra. Quanti giorni
aveva la luna?
Epatta anno 1849 = [8 + (1849 resto19)X11-18 + 4 + 6] resto 30 = 6.
Età luna 10 agosto 1849 = (1 + 5 + 6) resto 30 = 12.
La luna era quasi piena.
ESEMPIO 2. Garibaldi coi suoi mille partì da Quarto la notte dal 5 al 6
maggio 1860. La luna era piena?
RISPOSTA: L'età della luna, calcolata coll'epatta, era di 13 giorni, quasi
piena.
§ 26. Il concilio di Nicea fissò il 21 marzo quale giorno
dell'equinozio di primavera. Chiamò plenilunio pasquale il giorno della luna
piena, cioè con 14 giorni secondo l'epatta, che avviene il 21 marzo, o
immediatamente dopo. E fissò la Pasqua alla domenica seguente il plenilunio
pasquale. Si possono applicare le formule:
Plenilunio pasquale =
21 marzo + [29 -(Epatta + 6) resto 30] giorni.
Pasqua = plenilunio + (7 -S plenilunio) giorni.
§ 27. ESEMPIO 1. I Vespri siciliani. Nell'anno 1282,
martedì dopo Pasqua, nell'ora del vespro, i siciliani si rivoltarono contro il
tiranno. In quale giorno di quale mese?
Calcoliamo Epatta anno 1282 = 17.
Età della luna il 21 marzo = (21 + 0 + 17) resto 30 = 8 giorni.
Aggiungo 6 giorni:
Età della luna il 27 marzo = 14 giorni, plenilunio pasquale.
S (27 marzo 1282) = (27 + 3 + 4 + 1282 + 320) resto 7 = 5.
Il giorno del plenilunio fu di venerdì. Aggiungo 2 giorni; avrò Pasqua il 29
marzo; e il martedì dopo Pasqua fu il 31 marzo, come insegna la storia.
ESEMPIO 2. Petrarca vide Laura nel "mille trecentoventisette a punto, Su
l'ora prima il di sesto d'aprile" (sonetto CCXI). Verificare che questo
giorno è il lunedì prima di Pasqua (e non il venerdì, come dicono alcuni).
§ 28. Nella riforma gregoriana, sussiste la stessa regola per Pasqua
(§ 26), salvoché l'epatta è gregoriana (§ 24), colle
eccezioni:
Se il calcolo indica il 26 aprile, la Pasqua è al 19 aprile.
Se il calcolo indica il 25 aprile, e se il resto dell'anno per 19 è maggiore di
10, allora Pasqua è celebrata il 18 aprile.
La prima eccezione rende la Pasqua non posteriore al 25 aprile e si presenta
negli anni 1609, 1981, 2076, ecc.
La seconda eccezione rende nel periodo di 19 anni tutte le epatte differenti, si
si presenta nel 1954, 2049, ecc.
Queste due eccezioni non si presentano nella regola di Nicea, poiché la Pasqua
non viene mai oltre il 25 aprile, né nel periodo di 19 anni, due epatte sono
eguali.
§ 29. ESEMPIO. Pasqua nel 1924:
Epatta anno 1924 = 24.
Età luna il 21 marzo 1924 = (24 + 21) resto 30 = 15 giorni.
La luna è già decrescente. Aggiungo 29 giorni:
Età luna il 19 aprile = 14 giorni; plenilunio pasquale.
S (19 aprile 1924) = (19 + 6 + 2) resto 7 = 6, sabato. Aggiungo 1 giorno:
Pasqua è il 20 aprile 1924.
Ciò secondo l'epatta. Il calcolo astronomico indica le lune piene il 21 marzo 4
h 30 m, e 19 aprile 14 h 11 m, ora inglese.
Il calcolo della Pasqua, come è qui spiegato, è la versione in segni
matematici della regola di Nicea e di Gregorio. Si calcola l'epatta dell'anno,
il novilunio pasquale e la domenica seguente.
Alcuni libri di Aritmetica riproducono una regola data dal grande matematico
Gauss, nel 1800, in età di 23 anni. Ma non vi è spiegata la ragione ed il
significato dei singoli risultati che si ottengono durante il calcolo.
§ 30. Vogliamo costruire il calendario pel 1925.
Quest'anno è comune, perché 25 non è multiplo di 4, regola § 4.
Il suo settimanale, § 13, è (25 + 25 quot 4) resto 7 = 3.
Aggiungo 3 ai settimanali dei mesi, § 16, e sottraggo da 7 o da 14.
Ottengo la data delle prime domeniche dell'anno:
gennaio 4, febbraio 1, marzo 1, aprile 5, maggio 3, giugno 7, luglio 5, agosto
2, settembre 6, ottobre 4, novembre 1, decembre 6.
Epatta anno 1925 = [29 +(25 resto 19) X 11] resto 30 = 5.
Aggiungo questa epatta 5 alle epatte dei mesi, § 20, e sottraggo da 30.
Avrò la data delle lune nuove:
gennaio 25, febbraio 24, marzo 25, aprile 24, maggio 23, giugno 22, luglio 21,
agosto 20, settembre 19, ottobre 18, novembre 17, decembre 16.
La luna vera precede quella calcolata coll'epatta di frazione di giorno.
Età della luna il 21 marzo = 5 + 21 = 26 giorni.
Aggiungo 18 giorni:
Età della luna 8 aprile = (26 + 18) resto 30 = 14, luna piena pasquale.
Settimanale 8 aprile = (8 + 6 + 3) resto 7 = 3, mercoledì.
Aggiungo 4 giorni;
Pasqua del 1925 è il12 aprile = giorno (12 + 90 = 102) dell'anno.
Pentecoste = Pasqua + 49 d = giorno 151 dell'anno = 31 maggio.
Ceneri = Pasqua - 46 d = 25 febbraio.
Ascensione = Pasqua + 39 d = 21 maggio.
Corpus Domini = Pasqua + 60 d = 11 giugno.
§ 31. L' età della luna media in
(anno 1900 d 0+ x d) = (x + 28.271) resto 29.5305881.
x indica un numero positivo o negativo, intero o fratto. Il principio del giorno è l'ora 0, mezzanotte, al meridiano di Greenwich. L'età della luna vera può differire dalla media, in più, o in meno, di una frazione di giorno. Il divisore 29.530...d è una lunazione.
ESEMPIO 1: Calcolo con questa formula l'età della luna la notte di Natale
del 1924.
Colle formule del § 6, § 7, § 8, ho:
25dec.1924 = anno 1900 d 0 + (25 + 334 + 24 X 365 + 6) d
= anno 1900 d 0+ 9125 d
Aggiungo: 28.271
_________
9153. 271
300 lune = 8859.176
__________
294.095
9 lune = 265.775
_________
Resto = 28.320
alla lunazione 29.530
__________
manca 1.210
I prodotti del mese lunare per 300 e per 9 si leggono sui regoli di Nepero. I
prodotti parziali sono spinti a 3 decimali, sicché l'errore influisce solo
sull'ultima cifra.
Conchiudo che a mezzanotte precedente Natale del1924 la luna ha giorni 28 e
frazione, concordante col calcolo coll'epatta fatto al § 20 .
E aggiungendo ancora d 1.210, cioè 1 giorno e 5 ore, si ha la luna nuova il 26
decembre 1924, ore 5.
Questo per la luna media. La luna nuova vera avviene il 26 decembre 1924, ore 3
e 46 m. Ma questo calcolo della luna vera non è più elementare.
ESEMPIO 2. Facendo nella stessa formula, x = -710033, si trova l'età della luna il 1° gennaio anno -44, inizio del calendario di Giulio Cesare. Si trova il novilunio medio il 18 gennaio anno -44, ora 19. Il novilunio vero è posteriore di alcune ore. Ciò d'accordo colla storia esposta in § 3 e § 9 .
I numeri sono espressi in italiano colle parole 1 uno, 2 due,
3 tre, 4 quattro, 5 cinque, 6 sei, 7 sette,
8 otto, 9 nove, 10 dieci 100 cento, 1000 mille
.
Esse derivano dal latino 1 uno, 2 duo, 3 tres, 4 quatuor,
5 quinque, 6 sex, 7 septem, 8 octo, 9 novem,
10 decem, 100 centum, 1000 mille . In alcuni libri
sta scritto che l'italiano uno viene dal latino unus, il che,
letteralmente inteso, non è giusto; poche parole italiane derivano dal
nominativo latino; in generale derivano dai casi obliqui, e la forma più
prossima all'italiano è l'ablativo.
La stessa origine hanno le parole francesi: 1 un, 2 deux, 3 trois, 4 quatre, 5 cinq, 6 six, 7 sept, 8 huit, 9 neuf, 10 dix, 100 cent, 1000 mille .
Come pure le spagnuole: 1 uno, 2 dos, 3 tres, 4 cuatro, 5 cinco, 6 seis, 7 siete, 8 ocho, 9 nueve, 10 diez, 100 ciento, 1000 mil .
E le portoghesi: 1 um, 2 dous, 3 tres, 4 quatro, 5 cinco, 6 seis, 7 sete, 8 oito, 9 nove, 10 dez, 100 cento, 1000 mil .
Parimenti nel rumeno: 1 un, 2 doi, 3 trei, 4 patru, 5 cinci, 6 sese, 7 septe, 8 optu, 9 noua, 10 diéce, 100 suta, 1000 mie .
La lingua italiana contiene pure tutta la numerazione greca, in derivati:
1 en, L. (latino) hen - in hendecasyllabo, I. endecasillabo = verso di 11 sillabe. Greco monoV, mono - = unico, si trova in L. monacho, I. monaco, = colui che vive solo; monade = unità.; L. monarcha, I. monarca = comandante unico; monogamo = chi sposa una sola donna; monographia = scritto su un solo soggetto; monopolio = vendita unica; monotheismo = che ammette un solo Dio; monotono = di un solo tono.
2 duo di- : diedro = con due faccie; dilemma = con due assunzioni; diploma = duplicato; L. diptero, I. dittero = con due ali; disticho = di due versi.
3 treiV tri -: tripode = con tre piedi; triade = terna; trigonometria = misura dei triangoli.
4 tessareV tetra -: tetragono = con quattro angoli;tetraedro = con quattro facce.
5 pente pente : pentametro = verso di cinque misure; pentagono = con cinque angoli.
6 ex hex : L. hexaedro, I. esaedro = solido con sei faccie, cubo; L. hexagono, I. esagono = con sei angoli; L. hexametro ecc.
7 epta hepta : L. heptagono, I. ettagono, = poligono di sette angoli; L. hebdomadario, I. ebdomadario = della settimana.
8 oktw octo : L. octogono, I. ottagono, ottaedro.
9 ennea ennea : ennea-gono = poligono di nove angoli.
10 deka deca : deca-gono ; deca -metro = dieci metri; deca -gramma ; dècade = decina.
100 ekaton hecaton : hecatombe, I. ecatombe = sacrificio di cento buoi; Franc. hecto -gramme, I. ettogramma = cento grammi.
1000 cilioi chilioi : chiliade = migliaio; Francese kilo-mètre, I. chilometro = mille metri.
10000 muria myria : Francese myriagramme, I. miria-gramma .
Altri numeri greci viventi in Italiano:
11: L. hendeca-syllabo, I. endecasillabo .
12: dodeca-edro .
20: icos-a-edro .
50: pentecoste = cinquantesimo giorno a partire da Pasqua = Pasqua + 49 d.
Tutte le parole italiane derivate dal greco sono internazionali.
La lingua inglese contiene tutta la numerazione greca, nelle parole citate; e contiene tutti i numeri latini nei derivati: 1 un-ity, 2 du-al, 3 tri-angle, 4 quàdru-ple, 5 quinqu-ennial, 6 sex-tant, 7 septem-ber, 8 octo-ber, 9 novem-ber, 10 decem-ber, 100 cent-i-grade, 1000 milli-metre.
I numeri, come parole isolate, hanno in inglese la forma:
1 one, 2 two, 3 three, 4 four, 5 five,
6 six, 7 seven, 8 eight, 9 nine, 10 ten,
100 hundred, 1000 thousand .
La lingua tedesca parimenti contiene nei derivati, tutti i numeri greci e i
latini; nella lingua popolare si usano le parole:
1 ein, 2 zwei, 3 drei, 4 vier, 5 funf,
6 sechs, 7 sieben, 8 acht, 9 neun, 10 zehn,
100 hundert, 1000 tausend .
La lingua russa si scrive con un alfabeto simile al greco, da cui deriva, e il cui studio esige alcuni minuti. E allora nel vocabolario russo troviamo tutti i numeri greci e latini, nei derivati; in lingua popolare i numeri si pronunziano all'incirca: 1 ino -, 2 dva, 3 tri, 4 cetirie, 5 piat, 6 sest, 7 sem, 8 vosem, 10 desiat, 100 sto .
Risulta evidente una similitudine fra i nomi dei numeri in latino, greco,
nelle lingue germaniche, e nelle slave, cui appartiene il russo. La somiglianza
diventa più chiara paragonandoli coi nomi della lingua sanscrita:
1 eca, 2 dva, 3 eri, 4 ciatur, 5 pancian,
6 sas, 7 saptan, 8 astan, 9 navan, 10 dasan,
100 sala, all'incirca.
Mentre le lingue italiana, francese, spagnuola, portoghese, rumena, colle numerose lingue secondarie, dette dialetti, derivano in tempi storici dal latino, i linguisti ammettono una lingua preistorica, detta indo-europea, da cui derivano il latino, il greco, le lingue germaniche, le slave, il sanscrito, ed altre lingue dell'Asia.
Esaminando più attentamente la similitudine, si trova l' identità.
2 due comincia con d in latino, greco, russo e
sanscrito.
In Inglese troviamo in corrispondenza il t : duo two,
decem ten, dente tooth, doce
teach = insegnare; e in mezzo meno regolare: pede foot,
foot-ball = palla che si gioca coi piedi; corde heart,
ede eat =mangiare, ad at, quod
what.
3 tre comincia con t in latino, greco, russo, sanscrito, ma in inglese con th: tres three, tu thou, tecto thatch, dente tooth, pater father, mater mother .
5 cinque comincia con p in greco pente, in russo e sanscrito; e al p indo-europeo risponde regolarmente l'inglese f: pater father, pede foot, per for, pisce fish, lupo wolf, pelle fell, film = p ellicola. Si ritiene che il latino quinque derivi per assimilazione da un penque, che si trova in lingue italiche, p. es., nel nome Pontio (Pilato), che significa quinto.
6 e 7 cominciano per s in latino, inglese, tedesco, russo, sanscrito, cui corrisponde in greco h, o lo spirito aspro: sex hex; septem hepta; semicirculo hemicyclo; sede (sedia), hedra, poly-hedro = solido con molte sedi (facce); super hyper-bola; sopore somno, hypno-tismo.
L. septem novem decem rispondono al greco hepta ennea deca, cioè la sillaba em risponde al greco a ; anche ad en risponde -a : L. nomen, greco onoma-stico, L. centum greco he-caton ; I. in-nominato, greco an-onymo .
Greco hecaton deve essere decomposto in he-, che significa 1, e caton corrispondente a centum . Al c latino-greco risponde regolarmente h nelle lingue germaniche: L. centum inglese hundred (-red è un suffisso); capite head; citra hither; colle hill; corde heart; cornu horn.
1000 mille è espresso nelle varie lingue da nomi differenti. Ciò per le parole popolari; poiché tutte le nazioni di origine europea hanno il vocabolario scientifico latino-greco.
Le lingue europee sono strettamente collegate, e si possono studiare facilmente colla guida di queste relazioni. Il lettore può consultare utilmente:
Ing. C. CANESI, Vocabolario interlingua-italiano-inglese, Paravia 1921, il quale contiene 10.000 parole comuni al latino, all'italiano e all'inglese, scritte sotto la triplice ortografia, e che bastano a costituire una lingua intelligibile senza studio da chi conosce o il latino o l'inglese o un'altra lingua d'Europa, e interpretabile, in caso dubbio, col solo vocabolario latino.
Gli studiosi di matematica possono leggere con molto profitto l'articolo della prof. L. VIRIGLIO, Le parole italiane di matematica derivate dal greco, pubblicato nel Bollettino di Matematica, diretto dal prof. CONTI, anno 1919. Ivi si trova l'origine ultima, la scomposizione in elementi e il significato delle parole di cui facciamo uso continuo.
Lo scopo della matematica è di risolvere i problemi numerici che si incontrano nella vita pratica. Questi problemi interessano gli allievi molto più che i calcoli su numeri astratti, o su lettere, dei quali calcoli gli allievi non veggono alcuna applicazione, perché spesso non ne hanno.
Sonvi altre questioni, quali i quadrati magici, i giochi degli scacchi, che trovansi nei libri dei giochi, ed altre in matematica pura, che, senza applicazione pratica, riescono piacevoli ad alcuni; ma non debbono essere imposti agli altri.
Nel corrente anno 1923-24, i professori di matematica nelle scuole medie devono pure insegnare fisica e computisteria. Dopo pochi mesi, nelle loro riunioni periodiche nei locali dell'Università di Torino, essi si dimostrarono contenti, anzi entusiasti delle nuove disposizioni, che permettono di applicare la matematica pura, e di uniformare i differenti i linguaggi.
1. Da Torino a Milano in ferrovia sonvi chilometri 150, e da Milano a
Venezia chilometri 265. Quanti in tutto?
SOLUZIONE 1. km 150 + km 265 = km 415.
Si opera sulle grandezze, e il risultato è la risposta.
SOLUZIONE 2. 150 + 265 = 415; sonvi 415 km.
Si opera su numeri, e si risponde con una grandezza.
SOLUZIONE 3. 150 + 265 = 415 km.
Questa ultima scrittura è diffusissima nei libri di matematica applicata alla computisteria, ingegneria, fisica, ecc. Ma i matematici puri la dicono falsa, perché il numero astratto 150 + 265 non può essere eguale alla grandezza, o numero concreto 415 chilometri.
Coloro che usano la scrittura 3, la interpretano
(150 + 265 = 415) km.
La stessa questione fu trattata a pag. 22. La notazione 1 non si presta ad ambiguità, e dà come risultato la risposta.
2. Da Roma a Pisa sonvi km 334; da Pisa a Genova km 165; di qui a
Torino km 166; da Torino a Modane 105, ed altri 135 per arrivare a Culoz, e
fatti ancora 559 km, si arriva a Parigi. Di quanti chilometri consta il percorso
Roma - Torino - Parigi?
L'insegnante volenteroso, coll'orario delle ferrovie, o anche colla guida della
propria città, potrà variare questi problemi di addizione.
3. La guerra di Troia. Omero nel II canto della Iliade narra che i
Greci avevano condotte all'assedio di Troia le navi seguenti: I Beoti andarono
su 50 navi, i Miniei su 30, i Focei ne avevano 40 nere. I Locrei, sotto il
comando del veloce Aiace, 40; gli Abanti di Eubea 40; gli Ateniesi ne trassero
50, e 12 gli abitanti di Salamina. Quelli di Argo, guidati dal buon Diomede,
avevano 80 navi. Il re Agamennone ne condusse 100 da Micene, e 60 gli Spartani,
duce Menelao, cui Paride rapi la moglie Elena. 9(} profonde navi venivano da
Pilo, duce il vecchio Nestore. Gli Arcadi erano venuti su 60 navi; 40 veloci
venivano dall'Elide, 40 nere dalle isole Echinadi; 12 rosse ne guidava il saggio
Ulisse. Gli Etoli ne conducevano 40, 80 gli abitatori di Creta; 9 venivano da
Rodi, 3 da Sima, 30 profonde da Nisiro. Il veloce Achille guidava
i Mirmidoni di Ftia su 50 navi. Seguono 40 da Filace, 11 da Fere, 7 da Metone,
30 profonde da Tricca, sotto la guida dei figli di Esculapio, 40 da Ormenio, 40
da Argissa, 22 da Cifo. E 40 nere navi avevano i Magneti.
Quante erano le navi greche all'assedio di Troia?
RISPOST4: 1186.
4. Il governo d'Italia, dal 10 luglio 1918 al 30 giugno 1919 vendette:
26 407 648 000 fiammiferi di cera
2 595 450 000 fiammiferi di legno paraffinato
29 235 683 000 fiammiferi solforati.
Quanti in tutto?
5. L'altezza sul suolo della Torre Eiffel a Parigi, è di 300 metri,
quella dell'Obelisco di Washington di 169 metri, quella della Mole Antonelliana,
a Torino, di 164 metri. La più alta delle piramidi d'Egitto misura 142 metri,
la cupola ili San Pietro a Roma 132 metri.
Qual è la differenza delle altezze di due di questi edifici?
6. Piazza San Carlo in Torino è un rettangolo di lati 170 m e 75 m
Quanta è la sua area?
RISPOSTA: 170 m x 75 m = 12750 m2.
Si applica la regola "L'area d'un rettangolo vale il prodotto dei due
lati". Alcuni autori dicono "La misura dell'area d'un rettangolo vale
il prodotto delle misure dei due lati"; ma questa frase, più lunga,
risulta incompleta; la "misura di una grandezza" ha senso solo se si
enuncia il denominatore, detto unità di misura. Così "il valore d'una
frazione, il cui numeratore è 2 ", è frase senza senso.
Vedasi un mio articolo "Area de rectangulo" in Rassegna di
Matematica, Roma 1921.
L'insegnante, ove lo creda opportuno, può definire "prodotto di due
lunghezze è il rettangolo da esse compreso", secondo il linguaggio di
Euclide. La parola prodotto, in questo senso si trova in Herone, matematico
verso l'anno 150 a. C., e poi in tutti i matematici, fino agli ultimi tempi.
7. Per tenere accesa una lampada elettrica, detta di 50 candele,
occorre la potenza di 75 watt. La lampada rimanga accesa per 2 ore al giorno per
30 giorni, cioè per 60 ore. Per avere l'energia consumata dalla lampada,
moltiplico i watt per le ore, ed ottengo
75 watt X 60 ore = 4500 watt-ora = 45 ettowatt-ora.
E sapendo che questa energia si paga L. 0.07 per ogni etto-watt-ora, la spesa
dell'illuminazione ammonta a L. 3.15 al mese, oltre altre spese.
8. Cambi. -Nei giornali si legge: cambi alla borsa di Torino, il 22
gennaio 1924: Parigi 104.10; Svizzera 397.80; Londra 97.20; New York 23.07.
Ciò significa:
100 franchi francesi = 104,10 lire italiane,
o più semplicemente
franco francese = 1,041 lire
franco svizzero = 3,978 lire
sterlina = 97,20 lire
dollaro = 23,07 lire.
Valutare in franchi francesi la lira italiana, il franco svizzero, la sterlina,
il dollaro.
Si ha:
lira = franco fr. / 1,041 = 0,960 fr. francesi.
Sostituisco nelle altre eguaglianze:
franco svizzero = (3,978/10041) fr. fr. = 3,821 fr. fr.
9. Nello stesso giorno dell' esercizio precedente, la borsa di Parigi
quota: Italia 96,10; Svizzera 382; Londra 93,32, New York 22,11.
Valutare in lire italiane il franco francese, lo svizzero, la sterlina, il
dollaro.
Converrà che l'insegnante prenda i dati dall'ultimo giornale; risolvendo questi
problemi, l'allievo si esercita nelle moltiplicazioni e divisioni, si informa
della vita sociale, e impara la computisteria. Questa è una semplicissima
applicazione dell'aritmetica, ma in cui si usa un'altra nomenclatura, sicché
apparisce come una scienza nuova ai matematici puri.
Per calcolare 3,978/1,041 dell'esercizio precedente, possiamo calcolare 1/1,041,
e moltiplicare il risultato per 3,978; e si dice allora che si applica il metodo
di "riduzione alla unità". Oppure si divide 3,978 per 1,041, e si ha
il metodo delle "proporzioni". Questa nomenclatura, che in parte
rimonta ad Euclide, è un duplicato delle notazioni aritmetiche.
10. Data l'altezza,dell'albero maestro d'una nave, trovare l'età del
capitano.
È questo un celebre esempio di problema, dato come insolubile. Il
filosofo-matematico Richard se ne occupò nella Revue de Métaphisique a.
1920.
Il problema si risolve sapendo che quella nave si trovava presso Genova; alla
capitaneria di porto trovasi la descrizione delle navi che frequentano il porto.
Da questo registro deduciamo il nome della nave; in altro registro leggiamo il
nome del capitano, e dall'ufficio di anagrafe ricaviamo la sua età. Quasi tutti
i problemi che si presentano in pratica sono della natura di questo.
Chi deve risolverli, cercherà gli elementi che mancano; ovvero li supporrà,
dicendo ben chiaro che cosa suppone. Così il problema "dato lo statuto di
una società di assicurazione, trovarne il funzionamento futuro", è della
natura considerata.
Un problema simile è il seguente:
11. Si domanda quanto vale l'argento contenuto in una moneta d'argento
da una lira, coniata prima del 1914.
Per risolvere questo problema, dobbiamo cercare gli elementi che ci occorrono.
Dalle tavole delle monete italiane, si ha che la moneta da una lira pesa 5
grammi ed ha il titolo di 835/1000; cioè:
moneta da 1 lira = 0,835 X 5 grammi d'argento puro...(1).
Nei giornali leggo la borsa di Londra, 22 gennaio 1924 "argento 337/8"
Ciò significa:
oncia d'argento al titolo 925/1000 vale denari 337/8.
Dalle tavole di comparazione delle misure inglesi colle metriche, ho che
l'oncia, di cui qui si parla, vale 31,1 grammi.
Il denaro, che in inglese si scrive d, e si pronuncia penny
(plurale pence, e anche penny), vale la sterlina/240.
La borsa di quel giorno dà sterlina = 97,06 lire.
Quindi questa informazione inglese, tradotta in italiano, significa:
31,1X0,925 gr. d'argento puro=33,875 X 97,06/240 lire...(2).
Dalla (1) e (2) ricavo:
moneta da una lira
= 0,835 X 5 X 33,875 X 97,06/240/31,1/0,925 lire = 1,98 lire.
Siccome il valore intrinseco delle monete d'argento è oggi doppio del loro
valore nominale, esse sono scomparse dalla circolazione.
12. Negli ultimi giochi olimpici, nel 1920 ad Anversa, il campione
podista percorse 200 metri in 22 secondi. Quale fu la sua velocità in metri al
secondo, ed in chilometri all'ora?
La velocità vale lo spazio diviso pel tempo. Onde:
Velocità = 200 metri /22 secondi = 9,09 metri /secondo; che si legge 9,09 metri
al secondo.
Per avere la velocità all'ora, osservo che hora= 60 X 60 sec. Quindi velocità
= 9,09 X 3600 metri /hora = 32,7 km. /hora.
Però questo campione non avrebbe percorso 32 chilometri in un'ora, come risulta
dall'esempio seguente.
13. Negli stessi giochi olimpici, il campione della Maratona ottenne
il record 42600 metri in 2 h 32 m 35 s. Quale fu la sua velocità?
Essa vale 42 600 metri /2 h 32 m 35 s.
Riduco il tempo in frazione decimale di ore = 2,543 h.
Velocità = 42,6 km / 2,543 h = 16,7 km /h.
Questa velocità è inferiore alla precedente.
L'insegnante volenteroso, servendosi degli orarii delle ferrovie, delle gazzette dello sport, può far calcolare la velocità dei treni, delle ultime corse podistiche, di velocipedi, motocicli, automobili, aeroplani, con grande soddisfazione dei giovinetti.
14. Una donna ha comperato 4 chilogrammi di zucchero, a 5 lire al chilogramma. Quanto ha speso?
1° SOLUZIONE: 4 kg X (5 L / kg) = (4 X 5 = 20) lire.
I chilogrammi, ripetuti due volte, vanno via, e rimangono le lire. Così tutti
ragionano. La notazione dice che il kg una volta è fattore, e l'altra divisore.
2° SOLUZIONE: Se per 1 kg. spende 5 lire, per 4 kg spende 4 volte di più,
cioè 5 X 4 = 20 lire. Il risultato 20 L è omogeneo col moltiplicando 5, che
era unito alle lire.
Questa regola si trova in molti libri di Aritmetica.
3° SOLUZIONE: Se per 4 kg. a 1 lira al kg. spende 4 lire, allora a 5 lire al
kg. spende 5 volte di più, cioè
4 X 5 = 20 lire. Il risultato, che è delle lire, è omogeneo col
moltiplicatore, e non col moltiplicando 4 che era unito ai chilogrammi.
La cosa è naturale, poiché nel prodotto, possiamo commutare moltiplicando e
moltiplicatore.
Vedasi, su questa questione, in cui varie sono tuttora le opinioni, un mio
articolo Operazioni sulle Grandezze, in "Atti R. Accademia delle
Scienze" di Torino, 19 marzo 1922, tradotto in interlingua "latino
sine flexione" col titolo: Operationes super magnitudines, in
"Rassegna di Matematica", Roma 1922.
BURALI-FORTI, Aritmetica pratica, Torino, ed. Gallizio, 1913.
BANDINI e CIAMBERLINI, Elementi di Geometria, editori G. B. Paravia
& C., Torino, 1916.
CATANIA, Elementi di Aritmetica ed Algebra, ed. Giannotta, Catania.
Conclusione.
L'insegnante di buona volontà potrà combinare problemi simili e migliori
dei precedenti, onde rendere attraente lo studio.
La differenza fra noi e gli allievi affidati alle nostre cure sta solo in ciò,
che noi abbiamo percorso un più lungo tratto della parabola della vita. Se gli
allievi non capiscono, il torto è dell'insegnante che non sa spiegare. Né vale
addossare la responsabilità alle scuole inferiori. Dobbiamo prendere gli
allievi come sono, e richiamare ciò che essi hanno dimenticato, o studiato
sotto altra nomenclatura. Se l'insegnante tormenta i suoi alunni, e invece di
cattivarsi il loro amore, eccita odio contro sé e la scienza che insegna, non
solo il suo insegnamento sarà negativo, ma il dover convivere con tanti piccoli
nemici sarà per lui un continuo tormento. Ognuno si fabbrica la sua fortuna,
buona o cattiva. Chi è causa del suo mal, pianga se stesso. Così disse Giove,
e lo riferisce Omero, Odissea I, 34. Con questi principii, caro lettore e
collega, vivrai felice.
Data creazione: 2003
Ultimo aggiornamento: settembre 2007
html 4.01
Sito Web realizzato da Gianfranco Bo