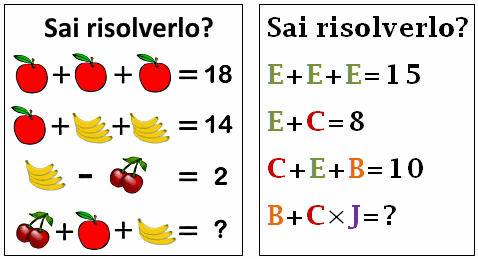
[BASE Cinque - Appunti di Matematica ricreativa]
Problemi non facilissimi che richiedono una piccola illuminazione
I problemi 5. e 6. hanno qualcosa in comune.
Cosa?
Due ragazzi devono attraversare un fiume, ma c'è una sola barca a remi che può trasportare un solo ragazzo alla volta.
La barca non può tornare indietro da sola.
Non ci sono corde o trucchi simili.
Nel fiume vivono pesci carnivori, perciò un ragazzo non può stare in acqua tenendosi alla barca.
Eppure entrambi i ragazzi riescono ad attraversare il fiume usando la barca.
Come si spiega?
(Tratto dal blog di Tanya Kovanova)
Ho disegnato alcuni triangoli su un foglio di carta.
Per prima cosa ho mostrato il foglio a Mario e gli ho chiesto quanti triangoli c'erano. Mario ha detto 5 e aveva ragione.
Poi ho mostrato il foglio a Sofia e le ho chiesto quanti triangoli c'erano. Sofia ha detto 3 e aveva ragione.
Ripeto che le risposte date date da Mario e Sofia sono entrambe esatte.
Come si spiega? Quanti triangoli ci sono sul foglio?
Puoi illustrare la tua spiegazione con un disegno.
(Tratto dal blog di Tanya Kovanova)
Sui social network, come FB si trovano molti esercizi come questi. Che ne dite di risolverli?
Attenti a non scivolare sulla buccia di banana!
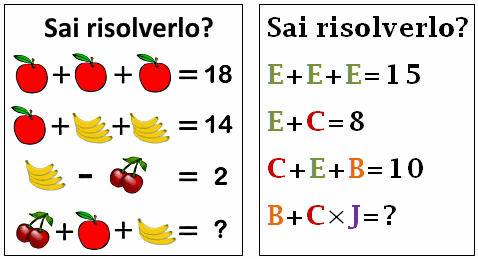
Su un tavolo ci sono i numeri da 1 a 9.
Aldo e Baldo prendono alternativamente un numero.
Vince il primo che ha tre numeri la cui somma è 15.
Chi fa la prima mossa a questo gioco, ha una strategia di vittoria sicura?
Nota. Ogni giocatore, durante il gioco, prende più di tre numeri. Per vincere è necessario e sufficiente che fra i numeri presi ce ne siano tre la cui somma sia 15. Naturalmente bisogna anche impedire che l'avversario ottenga 15 prima di noi.
Undici soldati sono disposti in un campo in modo che le distanze fra di loro, presi a due a due, siano tutte diverse.
A un certo punto il caporale (che non fa parte del gruppo) ordina: "Ciascuno di voi guardi il soldato più vicino!"
Su un tavolo c'è una riga di 10 monete, tutte in euro ma di valori non tutti uguali.
Quello che vedete qui sotto è soltanto un esempio.

Dimostrate che Alice può giocare in modo tale da garantirsi, alla fine, una somma di denaro non minore di quella di Bob.
Non si chiede di trovare la strategia migliore ma una strategia semplice, intutitiva, quasi immediata da realizzare e valida per un qualunque numero pari di monete.
(Problema tratto da: Peter Mann Winkler, Mathematical Puzzles: A connoisseur's collection, 2003).
.
.
.
7. Qualcosa in comune
Un foglio ha due lati, un fiume ha due rive. Affrontando questi problemi si tende a pensare che i due ragazzi si trovino sulla stessa riva e vogliano attraversare insieme e che i triangoli si ano disegnati sullo stesso lato del foglio.
6. Attraversare un fiume
I due ragazzi che volevano attraversare il fiume si trovavano su due rive opposte.
5. Quanti triangoli?
Ogni FOGLIO ha due lati. Su un lato ho disegnato 5 triangoli e sull'altro 3 triangoli. A Mario ho mostrato un lato e a Sofia l'altro.
4. Equazioni
Si ricava facilmente:
E=5
C=3
B=2
J rimane un mistero finché...
non si scopre che deve valere 10.
Perciò B+C*J=32
Questo esercizio richiede un po' di pensiero laterale per superare l'assuefazione a problemi come quello qui sotto, di cui sono pieni alcuni social network, tipo FB.

3. Somma 15
Risposta in breve.
Possiamo disporre i numeri da 1 a 9 in un quadrato magico in cui la somma di ogni riga, ogni colonna e ogni diagonale è 15.
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Per vincere bisogna riuscire a prendere i numeri di una riga o di una colonna o di una diagonale. Nello stesso tempo bisogna anche impedire che l'avversario faccia altrettanto.
Questo gioco quindi è equivalente al gioco del Tris.
Poiché per il Tris non esiste una strategia vincente ma solo una strategia per non perdere (ovvero per fare pari), tale strategia non esiste neppure per il gioco Somma 15, né per il primo né per il secondo giocatore.
Risposta dettagliata.
I gruppi di tre cifre a somma sono otto
{159, 168, 249, 258, 267, 348, 357, 456}
Le cifre che appartengono a due gruppi sono
{1, 3, 7, 9}
quelle che appartengono a tre gruppi sono
{2, 4, 6, 8}
mentre il 5 appartiene a quattro gruppi.
Consideriamo ora una griglia 3x3
| ... | ... | ... |
| ... | ... | ... |
| ... | ... | ... |
Essa è dotata di tre righe, tre colonne e due diagonali principali: ogni cella della griglia appartiene ad una riga e ad una colonna; in più, le celle ai vertici appartengono ad una diagonale mentre la cella centrale appartiene ad entrambe le diagonali. Sistemiamo il 5 (che appartiene a quattro gruppi) nella cella centrale
| ... | ... | ... |
| ... | 5 | ... |
| ... | ... | ... |
l’1 e il 9 (che appartengono a due gruppi) in due celle laterali opposte, il 3 e il 7 (che appartengono anch’essi a due gruppi) nelle altre due
| ... | 1 | ... |
| 3 | 5 | 7 |
| ... | 9 | ... |
e nelle celle ai vertici sistemiamo opportunamente le altre quattro cifre (che appartengono a tre gruppi)
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Ciò che abbiamo ottenuto è il quadrato magico Lo Shu, di antichissima tradizione: in detto quadrato magico, ogni riga, ogni colonna e le diagonali principali danno somma 15 (per costruzione).
Vale anche l’inverso: tre cifre danno somma 15 se e solo se sono disposte su una riga, una colonna o una diagonale principale (otto sono i gruppi di tre cifre di somma , otto le righe, colonne e diagonali principali).
Abbiamo trovato un isomorfismo tra il gioco “Somma 15” e il gioco del Tris: un giocatore, per vincere, deve prendere i tre numeri che stanno su una riga, una colonna o una diagonale principale.
Ed è ben noto che il gioco del tris finisce sempre pari se giocato razionalmente: quindi, il primo giocatore non ha una strategia di vittoria sicura.
(Panurgo)
2. Soldato non guardato
Invece di estendere il problema per generalizzarlo, faccio l'operazione inversa, riducendo l'universo ai minimi termini.
Abbiamo ora tre soldati. Due separati dalla distanza miniore (chiamiamoli A e B) si guardano l'un l'altro. Il terzo (C) guarda quello, tra i primi due, che è più vicino a lui. E nessuno guarda lui.
Adesso proviamo ad espandere pian piano il problema. Una voltra trattati i due primi soldati (quelli a distanza minima che si guardano l'un l'altro), andiamo a cercare la seconda distanza più corta. I casi sono due: o tra gli estremi di questa distanza c'è uno dei coinvolti nella prima distanza (chiamiamo questa seconda distanza C-B), o i due nuovi estremi sono due new entry (C e D). Nel primo caso stiamo ripetendo la situazione con solo tre soldati. Nel secondo caso, C e D si guardano tra di loro, e sarà il quinto (E) a dover guardare il suo viciniore senza essere ricambiato. Anche se ripartiamo dalla situazione dei tre, aggiungendone altri due, si ricasca nel solito bivio.
(Enrico Delfini)
Nota.
Peter Winkler dichiara che questo problema è tratto dalle competizioni matematiche di Voronezh (Russia), 1966.
La versione originale (tradotta in inglese), però era questa:
There is exactly one astronomer on every planet of a certain system. He watches the closest planet. The number of the planets is odd and all of the distances are different. Prove that there is one planet being not watched.
Fonte: http://pertselv.tripod.com/RusMath.html
1. Monete in riga
Numeriamo le monete da 1 a 10.
L' illuminazione consiste nel rendersi conto che Alice può sempre prendere tutte le monete di posizione dispari o tutte quelle di posizione pari, indipendentemente dalle scelte di Bob.
Infatti, indicando per comodità con D le monete di posizione dispari, e con P quelle di posizione pari, si ha che all'inizio, i due estremi sono di tipo (D, P).
Se Alice sceglie D, i nuovi estremi saranno di tipo (P, P), per cui Bob dovrà scegliere per forza P.
I nuovi estremi saranno quindi di nuovo di tipo (D, P) e Alice potrà scegliere di nuovo D.
E così via fino alla fine delle monete.
Stesso discorso, ovviamente, se Alice sceglie P all'inizio.
Pertanto, ad Alice basterà effettuare la somma delle monete di posizione dispari e la somma delle monete di posizione pari; dopo di che sceglierà di prendere il gruppo di monete con somma maggiore. (Pietro Vitelli)
---
Pace e bene a tutti!
Gianfranco Bo
Data creazione: dicembre 2011
Ultimo aggiornamento: maggio 2020
xhtml 1.1
Sito Web realizzato da Gianfranco Bo