[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Il bambù spezzato

Una ricreazione pitagorica nata in Cina?

Il bambù spezzato
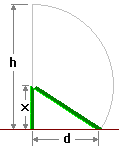
Una canna di bambù di altezza h si spezza ad una distanza x dal suolo.
La parte spezzata rimane attaccata al bambù per un'esile fibra e cade al suolo ruotando attorno al punto di frattura. L'estremo superiore della parte spezzata tocca il suolo ad una distanza d dalla base del bambù.

Calcolare x sapendo che h = 10 e d = 3.

Nota storica
La prima versione di questo problema si trova nel libro cinese Chiu Chang Suan Shu, Nove capitoli sulle arti matematiche di autore ignoto, risalente al 300-200 a. C.
Qualcuno sa risolverlo senza usare equazioni?

Il bambù spezzato: la versione originale
C'è un bambù alto 1 zhang la cui estremità superiore, essendo spezzata, tocca il terreno ad una distanza di 3 chih dalla base del fusto.
A quale altezza si trova la frattura?

Nota: 1 zhang = 10 chih

Illustrazione del Chiu Chang Suan Shu
tratta da G. Ghevergeese J., C'era una volta un numero, Il Saggiatore, 2000

Il bambù spezzato di Bhaskara
Un bambù alto 32 cubiti si è spezzato a causa del vento. La sua estremità superiore tocca il terreno ad una distanza di 16 cubiti dalla base del fusto.
Dimmi, o matematico, a quale altezza si trova la frattura?

Nota storica.
Questa versione del problema è attribuita all'indiano Bhaskara II, 1150.

L'albero spezzato di Filippo Calandri
C'è un albero alto 50 braccia sulla riva di un fiume largo 30 braccia.
Il caso vuole che l'albero si spezzi in un punto tale che la sua cima tocchi la riva opposta del fiume.
Voglio sapere quante braccia di albero si sono rotte e quanto ne rimane ritto.

Testo e immagine tratti dall'Aritmetica di Filippo Calandri, 1491


Ultimo aggiornamento: maggio 2007

Risposte & riflessioni

Il bambù spezzato
Per risolvere questo problema occorre applicare il teorema di Pitagora ed è interessante notare che la parte quadratica che compare nell'equazione risolutiva si elimina, lasciandoci un'equazione di primo grado.
Ricordiamo che c'è da calcolare x sapendo che h = 10 e d = 3.
Facendo riferimento alla figura, si ha:

(N.B. x^2 significa x elevato al quadrato)

x^2 + 9 = (10-x)^2

x^2 + 9 = 100 - 20x +x^2

20x = 91

x = 91/20

Il bambù spezzato: la versione originale
Grazie a Panurgo per la soluzione.

h = 1 zhang = 10 chih
a = 3 chih
b = 4,55 chih
c = 5,45 chih

Il bambù spezzato di Bhaskara
Grazie a Panurgo per la soluzione.

h = 32 cubiti
a = 16 cubiti
b = 12 cubiti
c = 20 cubiti

L'albero spezzato di Filippo Calandri
Grazie a Panurgo per la soluzione.

h = 50 braccia
a = 30 braccia
b = 16 braccia
c = 34 braccia

xhtml 1.1

Sito Web realizzato da Gianfranco Bo