[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Un problema antico risolto con un metodo moderno
La lunula di Ippocrate
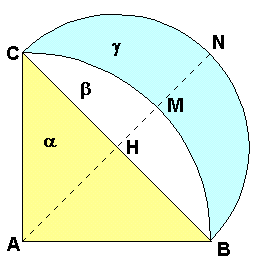
Osservate la figura qui sotto.

ABC è un triangolo rettangolo isoscele e H è il punto medio
dell'ipotenusa BC.
L'arco BMC è un quarto della circonferenza di centro A e raggio AB.
L'arco BNC è metà della circonferenza di centro H e raggio HB.
La figura delimitata dai due archi si chiama lunula o menisco.
Il pitagorico Ippocrate di Chio, vissuto nella seconda metà del quinto
secolo a. C. dimostrò che l'area della lunula BMCN è uguale a quella del
triangolo rettangolo ABC.
Chi sa fare altrettanto?
Nota storica.
Qual è l'elemento sorprendente della quadratura delle lunule, che colpisce
tanto noi oggi quanto stupì Ippocrate 2400 anni fa? La risposta ce la da
lo stesso Eudemo che, nel secondo libro della Storia della Geometria,
dice così: "Anche le quadrature delle lunole, per quanto sembrassero
riguardar figure non evidentemente quadrabili per la loro affinità col cerchio,
furono eseguite da Ippocrate, e apparvero condotte correttamente."
(citazione da: Pitagorici - Testimonianze e frammenti, a cura di Maria Timpanaro
Cardini, La nuova Italia, Firenze, 1973, Fasc. II, pag 43).
Per la precisione, l'opera di Eudemo andò distrutta e le parti giunte fino a
noi ci sono state tramandate da Simplicio, ma forse conviene fermarci
qui...
La lunula di Ippocrate

Indichiamo con a la lunghezza del cateto AB.
Per il teorema di Pitagora, abbiamo che CB = aÖ2, BH = (aÖ2)/2.
L'area del triangolo ABC è: a2/2
L'area della lunula è la
differenza fra le aree del semicerchio BNC e del settore circolare BMC.
Area semicerchio BNC = p·BH2/2 = pa2/4
Area settore BMC = p·AB2/4-
a2/2 = pa2/4
- a2/2
Area lunula = pa2/4 - pa2/4 + a2/2 = a2/2
Come si vede, i due termini pa2/4 si eliminano a vicenda e rimane a2/2, che è proprio l'area del triangolo rettangolo.
Sito Web realizzato da Gianfranco Bo