[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Scale incrociate

1. Scale incrociate facile
Due case si trovano l'una di fronte all'altra lungo una via piuttosto stretta.
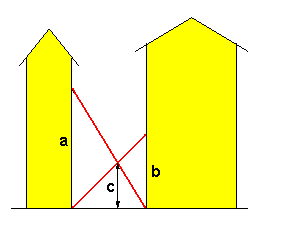
Ci sono inoltre due scale incrociate che partono dalla base di ciascuna casa e si appoggiano al muro della casa di fronte rispettivamente alle altezze a , b.
A quale altezza c si incrociano le due scale?
La figura qui sotto illustra la situazione.

2. Scale incrociate difficile
Due case si trovano l'una di fronte all'altra lungo una via piuttosto stretta.
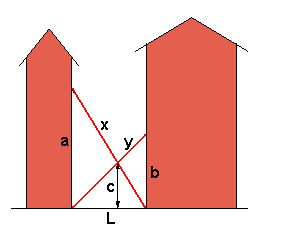
Ci sono inoltre due scale incrociate lunghe rispettivamente x = 30, y = 20 che partono dalla base di ciascuna casa e si appoggiano al muro della casa di fronte.
Il punto d'incrocio delle scale si trova ad un'altezza c = 10.
Quanto è larga la strada?
La figura qui sotto illustra la situazione.

Nota storica.
Le prime versioni di questi problemi risalgono a Mahavira 850, Bhaskara II 1150, Fibonacci 1202.

3. La scala e la scatola facile
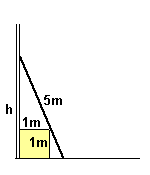
Una scatola cubica di 1 m di lato è appoggiata ad un muro.
Una scala lunga 5 m può essere appoggiata al muro in modo che la scatola si trovi sotto la scala.
Qual è la massima altezza a cui può giungere la scala?
La figura qui sotto illustra la situazione.

4. La scala e la scatola difficile
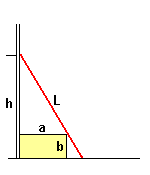
Una scatola alta b e larga a è appoggiata ad un muro.
Una scala lunga L può essere appoggiata al muro in modo che la scatola si trovi sotto la scala.
Qual è la massima altezza a cui può giungere la scala?
La figura qui sotto illustra la situazione.

Nota storica.
Le prime versioni di questi problemi risalgono a Simpson, Algebra, 1745.

Risposte & riflessioni

1. Scale incrociate facile
1/c = 1/a + 1/b

2. Scale incrociate difficile

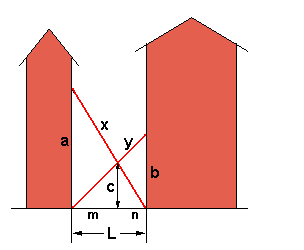
Applicando Pitagora ai triangoli rettangoli formati da ciascuna scala con il rispettivo muro a cui è appoggiata:
L^2 = x^2 - a^2 = y^2 - b^2
da cui:
x^2 - y^2 = a^2 - b^2

Osservando inoltre le similitudini opportune:
L/a = n/c
L/b = m/c
da cui:
L/a + L/b = (n + m)/c = L/c
e ancora:
1/a + 1/b = 1/c

Bisogna quindi risolvere il sistema:
x^2 - y^2 = a^2 - b^2
1/a + 1/b = 1/c

Nel nostro caso abbiamo: x = 30; y = 20; c = 10.
Infine si ottiene:
L =12.31185724

3. La scala e la scatola facile

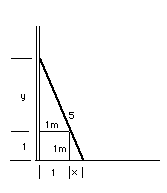
y = 1/x
(x+1)^2 + (y+1)^2 = 25

Ecco alcune soluzioni complete.

Montnoir, 21/03/05 18:29:06
Hmax = 4,84 (valore approssimato)
Qui l'equazione trigonometrica risolvente è
5*sin(x)- tg(x) - 1 = 0
da cui si ricava un angolo tra pavimento e scala di 1.316 rad.

Lucky, 21/03/05 20:09:33
Beh, c'è anche un modo geometrico per risolvere il problema:
si scrive l'equazione della retta passante per i punti A=(a,0) e B=(0,b) e si ottiene (forma parametrica):
x/a + y/b = 1
Poi si impone il passaggio per il punto P=(1,1). Si ottiene la condizione
1) 1/a + 1/b =1
che, associata all'altra,
a^2 + b^2 = 25
con pochi passaggi conduce all'equazione
(ab)^2 - 2ab - 25 = 0
la cui unica soluzione positiva è:
2) ab = [2+sqrt(104)]/2 = 6,099...
D'altra parte, dalla condizione 1) si ricava che è anche
(a+b) = 6.099...
da cui b = [2+sqrt(104)]/2 - a
che, sostituito nella 2), conduce all'equazione
a^2 - a[2+sqrt(104)]/2 + [2+sqrt(104)]/2 = 0
le cui due soluzioni positive
a1 = 4,838501161...
a2 = 1,260518353...
risolvono completamente il problema, rappresentando rispettivamente le distanze della cima e del piede della scala dal punto di intersezione della parete e del pavimento.

Lucky, 21/03/05 20:17:12
Dico meglio, rappresentano le distanze del piede della scala dalla parete nelle due posizioni possibili:
1) con la scala quasi orizzontale
2) con la scala quasi verticale.
E' chiaro che, per simmetria, la distanza della cima della scala dal pavimento ha gli stessi valori, ma invertiti.

Gianfranco Bo, 21/03/05 22:07:28
Complimenti, risposte esatte e soluzioni valide.
Buona quella di Lucky che rimane nell'ambito delle eq. di 2° grado.
Posto anche la mia soluzione, visto che ho faticato un po' a scriverla.
Indico con:
1+y la quota del punto in cui la scala tocca il muro;
1+x la distanza dalla base del muro del punto in cui la scala tocca il pavimento.
Applico il teorema di Pitagora:
(x+1)^2 + (y+1)^2 = 25
Ho un'equazione e due incognite, ma...
osservando dei triangoli simili, posso dire che:
1:y = x:1
ovvero, ecco la seconda equazione:
xy=1; y=1/x
ed ecco la risolvente (di 4° grado)
x^2 + 1/x^2 + 2x + 2/x - 23 = 0
x^4 + 2x^3 - 23x^2 + 2x + 1 = 0
x=0.2605183...
y=3.8385...
Per cui l'altezza massima è:
4.8385 m (circa)

4. La scala e la scatola difficile

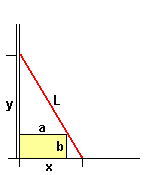
x^2 + y^2 = L^2
(x-a)(y-b) = ab