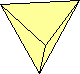
tetraedro
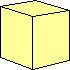
esaedro o cubo
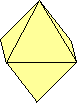
ottaedro
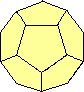
dodecaedro
icosaedro
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
I 13 poliedri archimedei o semiregolari
Partiamo dai 5 solidi platonici o regolari.

tetraedro |

esaedro o cubo |

ottaedro |

dodecaedro |

icosaedro |
Tronchiamo i vertici e otteniamo cinque poliedri troncati.
tetraedro |
cubo |
ottaedro |
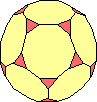
dodecaedro |
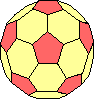
icosaedro |
I solidi archimedei sono in tutto 13 e traggono il loro nome da Archimede, che li ha trattati in un'opera ora perduta.
Il troncamento (di Archimede)
Una proprietà dei solidi archimedei: hanno tutti gli spigoli uguali.
I poliedri archimedei ottenuti troncando i poliedri platonici
1. Dal tetraedro all'ottaedro e viceversa
| troncare i vertici (TV) -->
|
troncare di più (TP) -->
|
|
2. Dal cubo all'ottaedro e viceversa
| TV -->
cubo |
<-- TP -->
cubo troncato |
<-- TP -->
cubottaedro |
<-- TP -->
ottaedro troncato |
<-- TV
ottaedro |
3. Dal cubottaedro al rombicubottaedro e viceversa
| TV -->
cubottaedro |
<-- TP -->
cubottaedro troncato |
<-- TV
rombicubottaedro |
4. Dal dodecaedro all'icosaedro e viceversa
| TV -->
dodecaedro |
<-- TP -->
dodecaedro troncato |
<-- TP -->
icosidodecaedro |
<-- TP -->
icosaedro troncato |
<-- TV
icosaedro |
5. Dall'icosidodecaedro al rombicosidodecaedro e viceversa
| TV -->
icosidodecaedro |
<-- TP -->
icosidodecaedro troncato |
<-- TV
rombicosidodecaedro |
Altri due poliedri archimedei
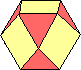
cubottaedro |
Ogni spigolo è sostituito da 2 triangoli equilateri. | 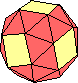
cubottaedro camuso |
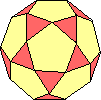
icosidodecaedro |
Ogni spigolo è sostituito da 2 triangoli equilateri. | 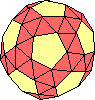
icosidodecaedro camuso |
| Nome e immagine | Facce | Spigoli | Vertici | Incidenza dei vertici |
|
|---|---|---|---|---|---|
| tetraedro troncato
|
8 | 4 triangoli 4 esagoni |
18 | 12 | 3,6,6 |
| cubo troncato o esaedro troncato
|
14 | 8 triangoli 6 ottagoni |
36 | 24 | 3,8,8 |
| ottaedro troncato
|
14 | 6 quadrati 8 esagoni |
36 | 24 | 4,6,6 |
| dodecaedro troncato
|
32 | 20 triangoli 12 decagoni |
90 | 60 | 3,10,10 |
| icosaedro troncato
|
32 | 12 pentagoni 20 esagoni |
90 | 60 | 5,6,6 |
| cubottaedro
|
14 | 8 triangoli 6 quadrati |
24 | 12 | 3,4,3,4 |
| icosidodecaedro
|
32 | 20 triangoli 12 pentagoni |
60 | 30 | 3,5,3,5 |
| rombicubottaedro
|
26 | 8 triangoli 18 quadrati |
48 | 24 | 3,4,4,4 |
| cubottaedro troncato
|
26 | 12 quadrati 8 esagoni 6 ottagoni |
72 | 48 | 4,6,8 |
| rombicosidodecaedro
|
62 | 20 triangoli 30 quadrati 12 pentagoni |
120 | 60 | 3,4,5,4 |
| icosidodecaedro troncato
|
62 | 30 quadrati 20 esagoni 12 decagoni |
180 | 120 | 4,6,10 |
| cubo camuso cubottaedro camuso (2 forme chirali)
|
38 | 32 triangoli 6 quadrati |
60 | 24 | 3,3,3,3,4 |
| dodecaedro camuso icosidodecaedro camuso (2 forme chirali)
|
92 | 80 triangoli 12 pentagoni |
150 | 60 | 3,3,3,3,5 |
ottobre 2005
Sito Web realizzato da Gianfranco Bo