[BASE Cinque - Appunti di Matematica ricreativa]

I cerini di Banach

Risolvete pure questo problema ma evitate di fumare!

Grazie a: Panurgo, Enrico Delfini, Franco, Pietro Vitelli per i contributi alla soluzione.

Nota: i cerini erano piccoli fiammiferi a base di cera utilizzati dai fumatori per accendersi le sigarette.

Il celebre matematico Stefan Banach soleva acquistare due scatole di cerini per volta. Ciascuna scatola nuova conteneva n cerini.
Se le metteva in tasca e prendeva i cerini scegliendo a caso una delle due scatole e rimettendola in tasca subito dopo.
Quando cercando un cerino trovava che la scatola scelta era vuota, gettava via le due scatole e ne comprava altre due.(*)

Le domande che si possono fare sono:

1. Qual è la probabilità che, quando il matematico estrae per la prima volta una scatola vuota, ci siano esattamente k cerini nell'altra scatola?
2. Quando il matematico estrae per la prima volta una scatola vuota, quanti cerini si aspetta di trovare nell'altra scatola?
3. Alla lunga, quanti cerini spreca in tutto il matematico?
4. Alla lunga, quanti cerini spreca in media il matematico per ogni coppia di scatole?

(*) Attenzione, il problema cambia se si suppone di andare a contare i fiammiferi dell'altra scatola, subito dopo aver acceso l'ultimo fiammifero di una scatola. Nel nostro caso si suppone che la scatola vuota sia rimessa in tasca insieme all'altra e, solo quando si cercherà di cavare da essa ancora un fiammifero, ci si accorgerà che è vuota. La formula si riferisce a tale situazione.

Variante proposta da Enrico.

A me avevano detto che buttava via le scatole quando prendeva l'ultimo cerino. E la cosa ha più (?) senso, perchè se gli succede di notte...

Risposte & riflessioni

Subito sotto il ritratto di Sefan Banach, riporto le risposte alle domande.

Seguono le spiegazioni di Enrico, Franco e Panurgo.

Stefan Banach

1. Qual è la probabilità che, quando il matematico estrae per la prima volta una scatola vuota, ci siano esattamente k cerini nell'altra scatola.
Risposta: supponiamo che le scatole inizialmente contengano n cerini.
Indico con p(k,n) la probabilità di rimanere con k cerini nell'altra scatola, quando si prende per la prima volta una scatola vuota.

2. Quando il matematico estrae per la prima volta una scatola vuota, quanti cerini si aspetta di trovare nell'altra scatola?
Risposta: 0 oppure 1 hanno la massima probabilità a pari merito.

3. Alla lunga, quanti cerini spreca in tutto il matematico?
Risposta: su 2^2n-1 coppie di scatole da n cerini c'è da aspettarsi di sprecarne in tutto a(n), secondo la seguente formula, (Simon Norton, 2001):

4. Alla lunga, quanti cerini spreca in media il matematico per ogni coppia di scatole?
Risposta: c'è da aspettarsi di sprecarne in media per ogni coppia di scatole cs(n), secondo la seguente formula:

Grazie a Enrico Delfini per la seguente spiegazione.

1) Con le scatole da un solo cerino, è molto banale, sia che si applichi l'algoritmo classico, sia quello modificato da me.
Nel caso classico, la prima scelta porta sempre ad una situazione 1-0, alla seconda sigaretta, c'è il 50% di probabilità di scegliere ciascuna scatola, per cui, nel 50% dei casi si aprirà quella ancora piena, e nel 50% si aprirà quella vuota, col risultato di buttare via anche il cerino rimasto nell'altra scatola.
(è un comportamento un po' stupido, ma...)
Nel caso modificato "ad usum Delfini", già alla prima sigaretta, si vuota una scatola, e si butta via anche l'altra, con lo spreco sicuro di un cerino
(e questo comportamento è ancora più stupido...)

2) Simulazione teorica con due scatole da tre cerini. Per sicurezza partiamo con un numero di esperimenti che sia una congrua potenza di due (essendo ogni volta una scelta dicotomica 50/50: per non fare troppi calcoli preventivi io sono partito con 128, ma possiamo limitarci a 16)
1° scelta-arriviamo (16 volte su 16) a 3-2
2° scelta- 8 casi 2-2 ; 8 casi 3-1
3° scelta- 8+4 casi 2-1 ; 4 casi 3-0
4° scelta- 6 casi 1-1 ; 6+2 2-0 ; 2 volte si apre quella vuota con 3 CERINI PERSI
5° scelta- 6+4 casi 1-0 ; 4 volte si hanno 2 CERINI PERSI
6° scelta- 5 volte si va allo 0-0 ; 5 volte si ha 1 CERINO PERSO

Il risultato finale è: 3 cerini persi 2 volte; 2 cerini persi 4 volte e 1 cerino per 5 volte: 19 cerini persi in 16 ripetizioni.

Grazie a Franco per la seguente spiegazione.

Io ti posso dire come sono arrivato alla soluzione, però sta a te valutare se è accettabile "per principianti" (io non ho esperienza di didattica).

Per prima cosa ho ipotizzato, come Enrico, un caso semplice di scatole da 3 cerini.

Mi sono fatto lo schema qui allegato per calcolare, sigaretta dopo sigaretta, quanti cerini potevano rimanere in ogni scatola e qual'era la probabilità di ogni posizione:

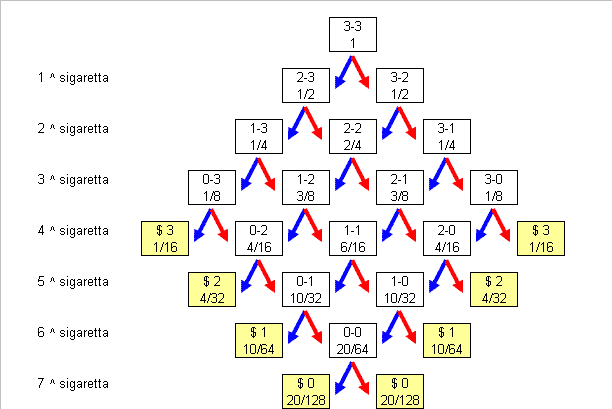
Con il simbolo $ ho indicato nelle caselle gialle il numero di cerini sprecati.

Il risultato finale è:

cerini sprecati = 3*1/16*2 + 2*4/32*2 + 1*10/64*2 + 0*20/128*2 = 19/16

A questo punto, per cercare di generalizzare, ho riscritto bene in grande la precedente addizione e ne ho osservato gli addendi:

3 * 1 / 8 + 2 * 4 / 16 + 1 * 10 / 32 + 0 * 20 / 64

Osservando il primo fattore di ogni addendo la successione è evidente:

Idem per i denominatori:

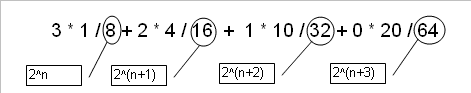
L'ultimo fattore, visto così sull'addizione, forse è meno intuitivo:

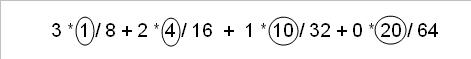
ma andando a guardare come avevo costruirlo il "rombo delle probabilità", associarlo ai coefficenti binomiali è stato immediato, così come a questo punto è stato immediato scrivere la formula finale:

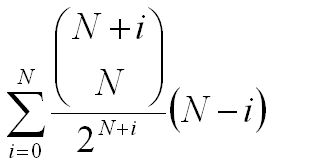
Ho fatto giusto una verifica per N=5 e ho postato la risposta incrociando le dita.

Grazie a Panurgo per la seguente spiegazione.

Questo è stato il mio ragionamento: non è particolarmente elementare; credo sia meglio impostarlo per un valore piccolo di n e mi piace in particolar modo la disposizione verticale del reticolo binomiale fatta da franco.

Le scatole di cerini di Banach sono indistinguibili, il prelievo di cerini non altera questa condizione e il modo in cui viene riposta la scatola dopo il prelievo, neppure. Con queste condizioni Banach si trova in uno stato di ignoranza e può quindi assegnare una probabilità alle proposizioni

A = è stata scelta la scatola A
B = è stata scelta la scatola B

in base al principio di indifferenza

$\left \{ p \left ( A \/ \middle | \/ I \right ) \/ = \/ p \left ( B \/ \middle | \/ I \right ) \\ p \left ( A \/ \middle | \/ I \right ) \/ + \/ p \left ( B \/ \middle | \/ I \right ) \/ = \/ 1\right . \qquad \Longrightarrow \qquad p \left ( A \/ \middle | \/ I \right ) \/ = \/ p \left ( B \/ \middle | \/ I \right ) \/ = \/ \frac 1 2$

Le sequenze di prelievo dei fiammiferi possono essere rappresentate su un reticolo binomiale

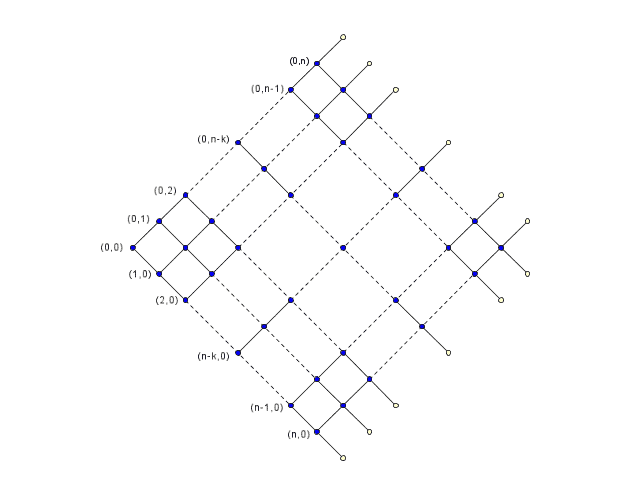
Ogni passo verso il basso corrisponde alla scelta della scatola A, ogni passo verso l'alto a quella della scatola B; i nodi bianchi corrispondono alla scelta di una scatola vuota.
Questa eventualità si può verificare solo dopo che da una scatola sono stati prelevati tutti gli n cerini che la scatola conteneva: supponiamo che ciò sia avvenuto dopo che dall'altra scatola sono stati tolti n-k cerini (siamo nel nodo rosso della figura seguente

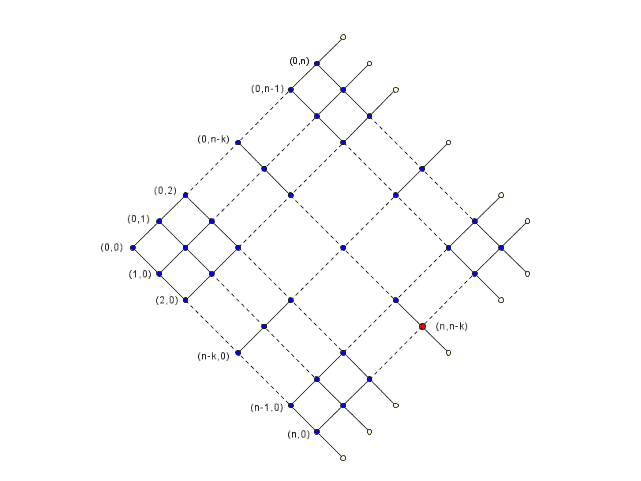
Ci sono ${{2n - k} \choose n}$ percorsi nel grafo che raggiungono tale punto, ciascuno formato di 2n-k scelte tra le scatole A e B: la probabilità di raggiungere il nodo (n, n-k) vale

$p \left ( \left ( n, \/ n \/ - \/ k \right ) \/ \middle | \/ I \right ) \/ = \/ {{2n - k} \choose n} \/ \left ( \frac 1 2 \right )^{\script 2n - k}$

La scelta della scatola vuota ha una probabilità di 1/2; poiché questo nodo corrisponde ad avere un resto di k cerini nell'altra scatola, la probabilità di avere tale resto quando la scatola scelta è vuota vale

$p \left ( k \/ \middle | \/ \left ( n, \/ n \/ - \/ k \right ) \/ I \right ) \/ = \/ \frac 1 2 \/ {{2n - k} \choose n} \/ \left ( \frac 1 2 \right )^{\script 2n - k}$

In realtà, però, il nodo (n, n-k) non è distinguibile dl nodo (n-k,n) che corrisponde ad aver vuotato la scatola B (le due scatole sono indistinguibili

Per simmetria, la probabilità di aver vuotato la scatola B è uguale a quella di aver vuotato la scatola A e la probabilità di avere un resto di k cerini è pari a

$p \left ( k \/ \middle | \/ I \right ) \/ = \/ p \left ( k \/ \middle | \/ \left ( n, \/ n \/ - \/ k \right ) \/ I \right ) \/ + \/ p \left ( k \/ \middle | \/ \left ( n \/ - \/ k, \/ n \right ) \/ I \right ) \/ = \/ {{2n - k} \choose n} \/ \left ( \frac 1 2 \right )^{\script 2n - k}$

Il valore atteso di k si calcola mediante la

$\left \langle k \right \rangle \/ = \/ \sum_{\script k = 0}^{\script n} k \/ p \left ( k \/ \middle | \/ I \right ) \/ = \/ \sum_{\script k = 0}^{\script n} k \/ {{2n - k} \choose n} \/ \left ( \frac 1 2 \right )^{\script 2n - k} \/ = \/ 2^{\script - 2n} \/ \sum_{\script k = 0}^{\script n} k \/ 2^{\script k} \/{{2n - k} \choose n}$

ovvero, dopo quanto trovato nel terzo volume della Bibbia¹

$\left \langle k \right \rangle \/ = \/ \frac {2n + 1} {2^{\script 2n}} {{2n} \choose n} \/ - \/ 1$

¹The Old Testament, the New Testament and the Encyclopedia of Integer Sequences

Grazie a Pietro Vitelli per la seguente spiegazione.

Il mio ragionamento è il seguente:
la probabilità, in un dato istante, di prendere un cerino da una delle due scatole è la stessa, ossia 1/2.
Ora indichiamo con la parola percorso, ogni possibile sequenza di cerini presi dalle tasche di Banach, che fa si che una delle due scatole resti vuota.
Quindi considerando un qualsiasi percorso, chiamiamolo c, la probabilità che questo percorso si verifichi ci è data, semplicemente, da:

(probabilità di scegliere un cerino da una delle due scatole) elevato a (numero di cerini del percorso +1)

ossia:

dove l (elle) è il numero di cerini del percorso c (il +1 dell'esponente è dovuto al fatto che dopo aver scelto l'ultimo cerino, la scatola, diventata vuota, viene rimessa in tasca).

Appare evidente che, affinché una scatola resti vuota, e nell'altra restino k cerini, il percorso scelto deve essere una sequenza di 2n-k cerini;
ora i possibili percorsi, lunghi esattamente 2n-k cerini, sono molteplici, e sono tutti equiprobabili.
La loro probabilità di verificarsi, per quanto detto poco più sopra, vale:

$p(c)\/=\/$\frac 1 2$^{l\small{+1}}\/\quad\Rightarrow\quad\/$\frac 1 2$^{2n-k\small{+1}}$

ora il numero di percorsi possibili, formati da 2n-k cerini, ci è dato da dalle combinazioni di 2n-k elementi in classe n, ossia:

(questo fatto non è immediato, ma si può comprendere cominciando ad elencare tutti i possibili percorsi formati da 2n-k cerini), il tutto moltiplicato per 2 data la simmetria del sistema (le due scatole sono interscambiabili).

A questo punto, la probabilità di avere una scatola vuota, e l'altra con esattamente k cerini ( p(k) ), equivale alla probabilità di scegliere almeno uno dei percorsi lunghi esattamente 2n-k cerini, ossia:

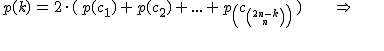
Da qui, il numero di cerini sprecati, in media, da Banach, come già scritto da Panurgo, ci è dato dal valore atteso di k, ossia:

Data creazione: agosto 2007

Ultimo aggiornamento: ottobre 2007

xhtml 1.1

Sito Web realizzato da Gianfranco Bo