
[BASE Cinque - Appunti di Matematica ricreativa]
Aldo dice la verità 3 volte su 4 (e quindi mente 1 volta su 4).
Baldo dice la verità 7 volte su 10 (e quindi mente 3 volte su 10).
Un dado viene lanciato sotto gli occhi di Aldo e Baldo.
Entrambi testimoniano che è uscito il 6.
Calcola la probabilità che sia davvero uscito il 6 | sapendo che entrambi i testimoni hanno dichiarato che è uscito il 6.

Prima di tutto dobbiamo chiarire cosa intendiamo per "dire la verità" e "mentire", in questa situazione.
Costruiamo il grafo della situazione. Attenzione, ho scritto solo i dati necessari a risolvere il problema.
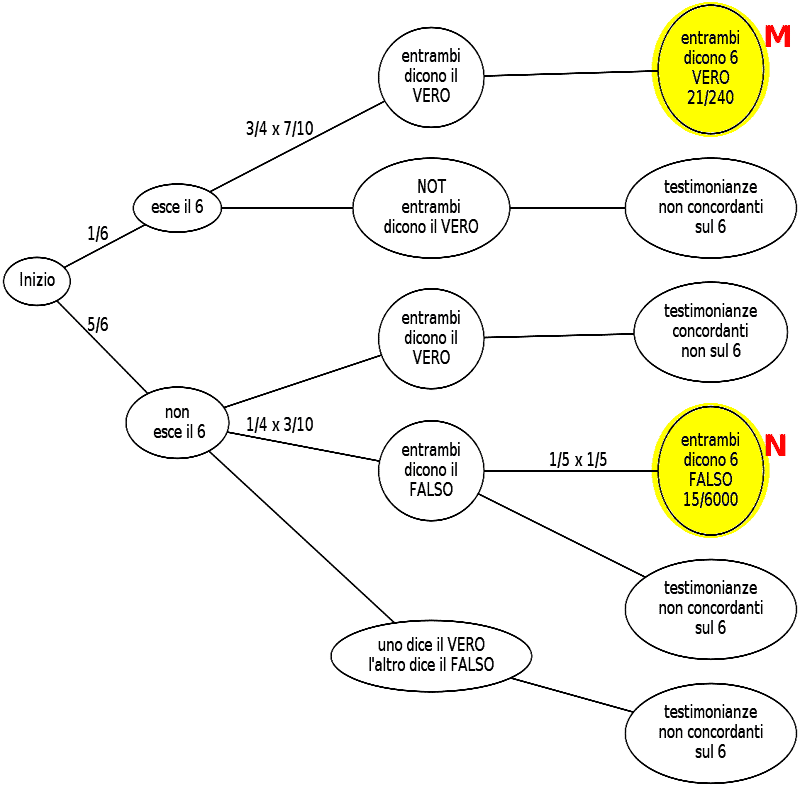
L'ipotesi iniziale è:
A = "E' davvero uscito il 6."
La sua probabilità a priori è ovviamente 1/6.
Ma noi abbiamo un'informazione in più:
E = "Entrambi i testimoni hanno dichiarato che è uscito il 6."
Dobbiamo calcolare la probabilità a posteriori della nostra ipotesi:
P(A | E) = "E' davvero uscito il 6 sapendo che entrambi i testimoni hanno dichiarato che è uscito il 6."
Osserviamo il grafico e applichiamo la regola di Bayes.
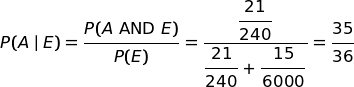
Ripetiamo il calcolo con un ragionamento statistico. Osserviamo il grafico, e rispondiamo alle domande.
Con quale probabilità entrambi dicono che uscito il 6?
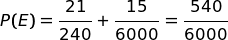
Con quale probabilità è uscito davvero il 6 quando entrambi dicono che è uscito il 6?
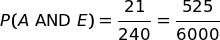
Ora, possiamo ragionare statisticamente così: su 6000 prove, entrambi i testimoni dicono "6" 540 volte, ma solo 525 di queste volte è uscito davvero il 6. La probabilità della nostra ipotesi condizionata è data dal rapporto fra i nue numeri.
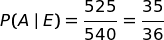
Qual è il modo più breve per calcolare la probabilità richiesta?
Sempre osservando il grafo, abbiamo:
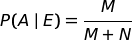
Nota.
Il problema è tratto e adattato da Henry Sinclair Hall, Samuel Ratcliffe Knight, Higher Algebra a Sequel to Elementary Algebra for Schools, Macmillan, 1894.
Parti del libro si possono consultare su Google books.

Data creazione: agosto 2014
Ultimo aggiornamento: agosto 2014
xhtml 1.1
Sito Web realizzato da Gianfranco Bo