
[BASE Cinque - Appunti di Matematica ricreativa]
Due cacciatori, Aldo e Baldo, durante una partita di caccia, vedono un orso e gli sparano contemporaneamente.
L'orso muore, ma c'é un solo foro di proiettile sul suo corpo.
Nelle condizioni del caso:
I due amici vendono la pelle dell'orso per 70 rubli.
Qual è il modo matematicamente corretto di dividere la somma di denaro fra Aldo e Baldo?

Conveniamo di considerare impossibile che i due proiettili siano entrati in uno stesso foro. Si deduce quindi che uno solo dei due cacciatori ha colpito l'orso. Ma non si sa chi è stato. E non si saprà mai con certezza.
Conveniamo allora di dividere i soldi in parti proporzionali alle probabilità a posteriori che ciascuno dei due amici sia stato la causa della morte dell'orso.
Indichiamo con E, A, B, rispettivamente gli eventi:
E = "Uno solo dei due cacciatori ha colpito l'orso."
Aldo = "Solo Aldo ha colpito l'orso."
Baldo = "Solo Baldo ha colpito l'orso."
Le probabilità a priori sono le seguenti:
La probabilità totale dell'evento E = "Uno solo dei due cacciatori ha colpito l'orso" è:
P(E) = 0,48 + 0,08 = 0,56
Cominciamo col calcolare la probabilità a posteriori della seguente ipotesi:
P(Aldo | E) = probabilità che "Aldo ha centrato l'orso, dato che uno solo dei due cacciatori ha colpito l'orso"
Applichiamo la formula di Bayes.
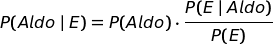
C'è un piccolo problema: quanto vale P(E | Aldo)?
P(E | Aldo) = probabilità che "Uno solo dei due cacciatori ha colpito l'orso" dato che "Solo Aldo ha colpito l'orso"
In questo caso, è evidente che Aldo implica E, perciò:
P(E | Aldo) = 1
Finalmente possiamo calcolare le probabilità a posteriori.
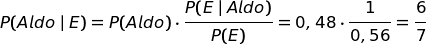
E di conseguenza:
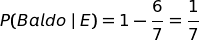
Segue la risposta alla domanda del problema:
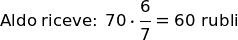
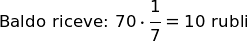
Note.
Questo problema è tratto da: E. S. Wentzel, Probability Theory - First Steps, MIR, Moscow, 1977, 1982 (translated from the Russian by N. Deineko).

Quali sono le origini di questo problema?
Andando a caccia di notizie sull'origine di questo problema ho trovato che un problema simile si trova nel testo:
Aram Arutiunovich Sveshnikov, Problems in Probability Theory, Mathematical Statistics, and Theory of Random Functions, pubblicato per la prima volta (?) in russo nel 1965 e tradotto in inglese nel 1968. (alcune pagine si possono consultare su google books).
A pag 29, il problema 7.9 parla di tre cacciatori che sparano contemporaneamente a un cinghiale. Una sola pallottola colpisce il cinghiale. Le probabilità di fare centro da parte di ciascuno dei cacciatori sonop rispettivamente 0.2, 0.4 e 0.6.
Si chiede di calcolare la probabilità che il proiettile che ha colpito il cinghiale sia rispettivamente del primo, del secondo e del terzo cacciatore.

Un'altra variante del problema della caccia all'orso è il seguente.
Tre frecce vengono lanciate contemporaneamente contro un bersaglio da tre arcieri.
Poiché i tre arcieri sono a distanza diversa dal bersaglio, si stima in:
Se una e una sola freccia colpisce il bersaglio, qual è la probabilità che sia dell'arciere A?
Precisiamo che le frecce sono identiche e non ci sono testimoni che ne hanno seguito le traiettorie. Perciò non è possibile stabilire con prove certe a chi appartiene la freccia che ha colpito il bersaglio.
Risposta: 3/13=23% circa
Il problema dei tre arcieri è stato risolto dettagliatamente:
a) da Giorgio Pietrocola, nel sito Maecla (http://www.maecla.it/matematica/iperproblema/index.htm)
b) da Panurgo, nel FORUM di BASE Cinque (http://www.base5forum.it/tre-arcieri-tre-freccie-una-freccia-t7760.html).
Data creazione: 2013
Ultimo aggiornamento: 2014
xhtml 1.1
Sito Web realizzato da Gianfranco Bo