
[BASE Cinque - Appunti di Matematica ricreativa]
Baldo dice la verità 4 volte su 5.
Baldo estrae a caso un numero della tombola e afferma che è uscito il 35 (I numeri della tombola sono i numeri interi da 1 a 90)
Qual è la probabilità che sia davvero uscito il 35 | sapendo che Baldo ha detto "35"?

Prima di procedere dobbiamo chiarire cosa intendiamo per "dire la verità" e "mentire", in questa situazione.
In particolare, nei casi in cui il numero uscito NON è 35, chi mente dice "35" con probabilità 1/89.
Costruiamo il grafo della situazione.
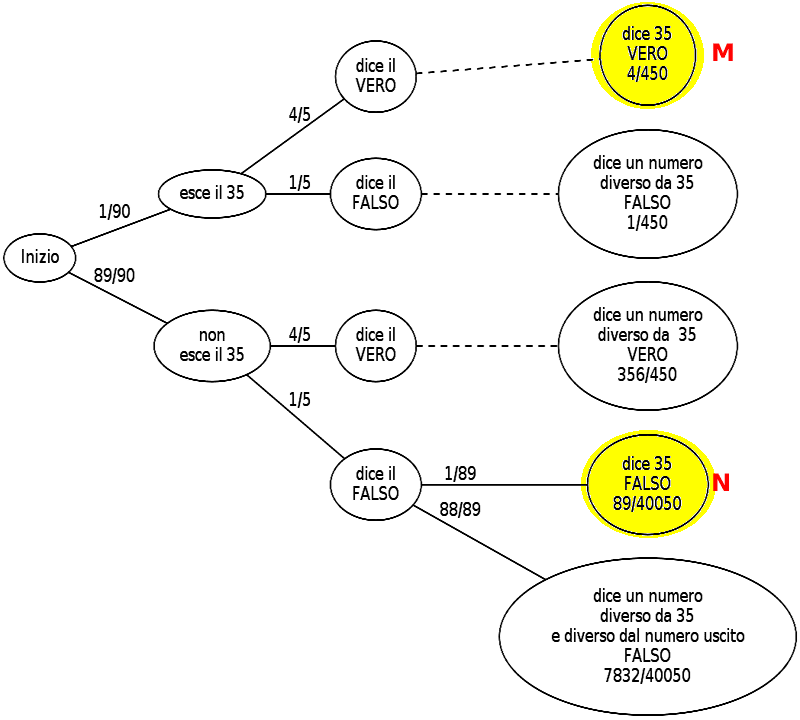
Chiariamo bene la domanda: vogliamo calcolare la probabilità dell'ipotesi:
A = "E' uscito il 35."
condizionata al fatto che:
E = "Baldo ha detto che è uscito il 35."
In simboli:
P(A | E) = Probabilità che "E' uscito il 35" sapendo che "Baldo ha detto che è uscito il 35."
Applichiamo la regola di Bayes (con la probabilità composta).
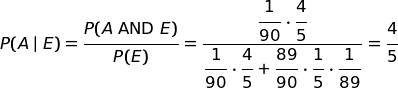
Rifacciamo il calcolo con un ragionamento di tipo statistico-proporzionale.
Osserviamo il grafico, e rispondiamo alle domande.
Con quale probabilità Baldo dice "E' uscito il 35"?
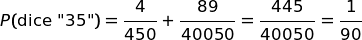
Con quale probabilità è uscito davvero il 35 quando Baldo dice che è uscito il 35?

La probabilità della nostra ipotesi è il rapporto delle due probabilità e risulta 4/5.
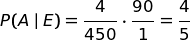
Oppure possiamo ragionare statisticamente così: su 450 prove, Baldo dice "E' uscito il 35" 5 volte, ma solo 4 di queste volte è uscito davvero il 35. La probabilità della nostra ipotesi è data dal rapporto fra i due numeri.
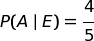
In che modo il grafo può aiutarci per semplificare e generalizzare il calcolo?
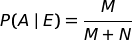
Nel problema precedente, abbiamo visto che i numeri abbastanza alti, che esprimevano probabilità legate alla tombola, si semplificano tutti e alla fine il risultato sembra dipendere soltanto dalla probabilità con cui Baldo dice il vero o mente.
Proviamo allora a generalizzare così:
Riprendiamo il grafo precedente intoducendo le variabili al posto dei numeri.
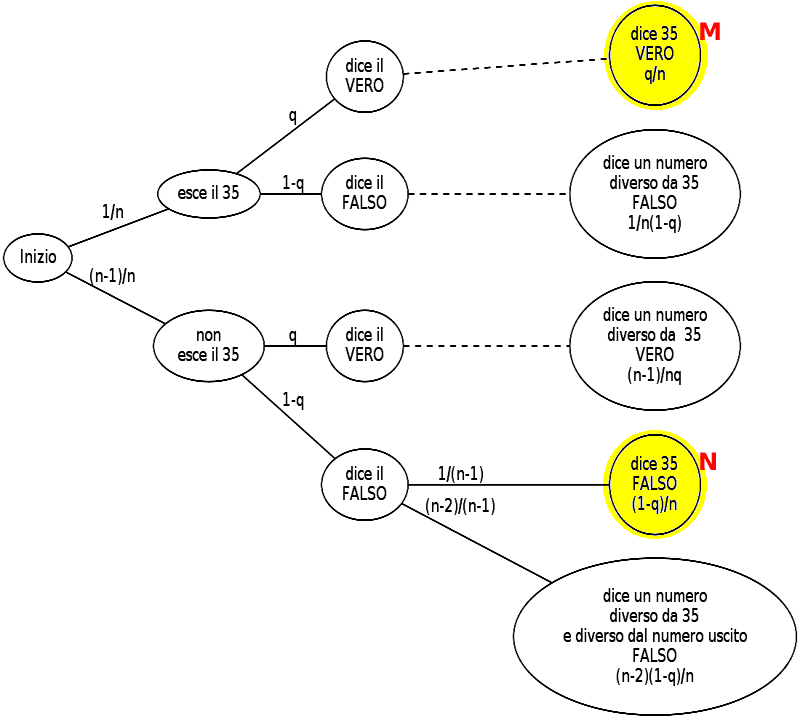
Passiamo senza indugio al calcolo finale, osservando che non dipende da n, anzi è proprio q.
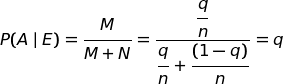
Nota.
La soluzione di questo problema è discutibile.
Infatti, se ammettiamo che quando NON esce il 35 e Baldo mente, possa mentire in un solo modo, dicendo sempre che è uscito il 35, allora la soluzione di questo problema evidentemente cambia.
Un esempio di questa impostazione si trova in: Autori Vari, Xam Idea Mathematics, FK Publications, New Delhi, 2009.
La risposta è 3/8, mentre con il metodo visto sopra dovrebbe essere 3/4.
Il punto dove c'é differenza fra le due soluzioni è quello tra le parentesi arancione.

Se Baldo ha soltanto due possibilità di esprimersi, per esempio A oppure NON-A (vero o falso), allora la soluzione del problema è come quella dell'esempio citato nella nota precedente.
Consideriamo per esempio il seguente problema.
Il grafo della probabilità è il seguente.
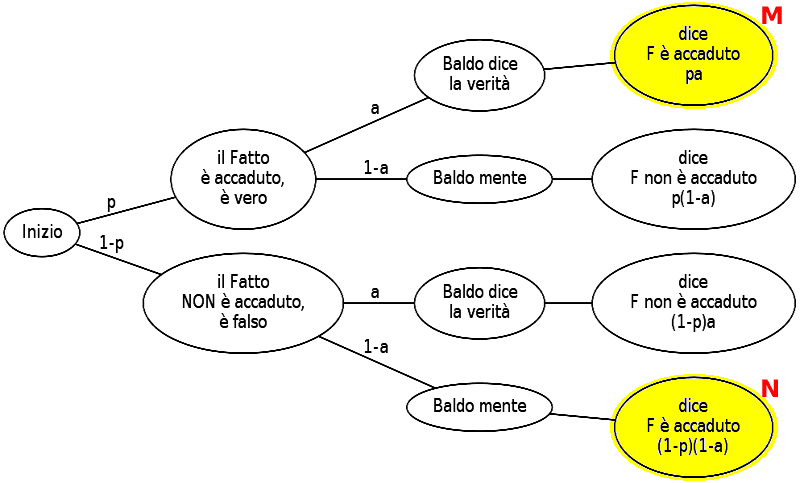
Indicando con:
bisogna calcolare il rapporto:
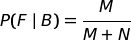
che, con le variabili in gioco, diventa:
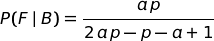
Per esempio, se:
allora:
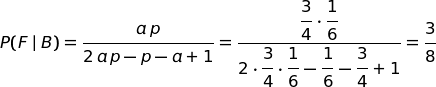
Data creazione: agosto 2014
Ultimo aggiornamento: agosto 2014
xhtml 1.1
Sito Web realizzato da Gianfranco Bo