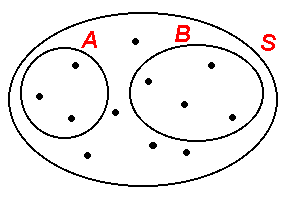
Eventi incompatibili
[BASE Cinque - Appunti di Matematica ricreativa]
Attenzione: questa è una breve sintesi elementare e nulla più.
In un sacchetto ci sono 7 palline bianche e 3 palline nere. Tranne che nel colore, le palline sono identiche: sono fatte dello stesso materiale, hanno le stesse dimensioni, sono perfettamente sferiche, ugualmente levigate e così via.
Infilerò una mano nel sacchetto, senza guardarvi dentro, e estrarrò una pallina a caso.
Qual è la probabilità che la pallina estratta sia nera?
L'evento "pallina estratta nera" ha perciò 3 possibilità su 10 di verificarsi.
Definisco la sua probabilità come il rapporto tra i casi favorevoli e quelli possibili e ottengo:
probabilità (pallina nera) = 3/10 = 0,3 = 30%
La risoluzione di questo problema ci fornisce lo spunto per dare una definizione di probabilità di un evento.
La probabilità che si verifichi un dato evento (E) è il
rapporto fra il numero (s) dei casi
favorevoli all'evento stesso e il numero (n) dei casi
possibili, purché tutti i casi considerati siano ugualmente
probabili.
(Guido Castelnuovo, Calcolo delle probabilità, Zanichelli)
p = p(E) = s/n
Esempio 1. Lanciando una moneta, qual è la probabilità che
esca testa?
I casi possibili sono 2, testa e croce {T, C}, i casi favorevoli sono 1 {T}
p(testa) = 1/2
Esempio 2. Lanciando un dado, qual è la probabilità che
esca il 5?
I casi possibili sono 6, {1, 2, 3, 4, 5, 6}, i casi favorevoli sono 1 {5}
p(5) = 1/6
Esempio 3. Estraendo una carta da un mazzo di 40, qual è la
probabilità che sia una figura?
I casi possibili sono 40, i casi favorevoli sono 12, perché le figure sono
12
p(figura) = 12/40
Esempio 4. Al gioco del lotto, qual è la probabilità che
esca un numero dato, in una estrazione di 5 numeri?
I casi possibili sono tutte le cinquine, i casi favorevoli sono le cinquine che
contengono il numero dato.
a) totale cinquine = combinazioni di 90 elementi a 5 a 5 = 90! / (5! · 85!)
b) totale cinquine con numero fisso = combinazioni di 89 elementi a 4 a 4 = 89!
/ (4! · 85!)
p(estratto al lotto) = 90! / (5! · 85!) / 89! / (4! · 85!) =
5/90
Per definire la probabilità si usa il concetto di eventi equiprobabili.
Questo non va bene perché per definire un concetto non si può usare il concetto stesso, altrimenti la definizione diventa circolare. E non definisce niente.
Perciò è necessario chiarire che cosa si intende per eventi equiprobabili.
A tale scopo si può introdurre il concetto del principio della ragione non sufficiente o principio di indifferenza, il quale asserisce che:
dato un gruppo di eventi, se non ci sono valide ragioni per pensare che qualche evento si verifichi più o meno facilmente degli altri, allora tutti gli eventi del gruppo si devono considerare equiprobabili.
Nota. Per calcolare il numero dei casi possibili e di quelli favorevoli, in molti casi serve il calcolo combinatorio. Per una semplice introduzione, vedi le seguenti pagine, su questo sito:
Permutazioni, disposizioni, combinazioni
La probabilità di un evento p(E) è sempre un numero compreso fra 0 e 1:
0 <= p(E) <= 1
Un evento che ha probabilità 0 è detto evento impossibile.
Un evento che ha probabilità 1 è detto evento certo.
Esempio 1. Estraendo una carta da un mazzo di 40, qual è la
probabilità che sia un 10 di cuori?
I casi possibili sono 40 i casi favorevoli sono 0, perché nei mazzi da 40 carte
non ci sono i numeri 8, 9, 10.
p(10 di cuori) = 0/40 = 0
Esempio 2. Estraendo una pallina da un'urna che contiene 8
palline rosse, qual è la probabilità che la pallina estratta sia rossa?
I casi possibili sono 8 i casi favorevoli sono 8, perché le ci sono 8 palline
rosse.
p(pallina rossa) = 8/8 = 1
La probabilità di un evento si può esprimere:
a) come frazione, ad esempio 3/4
b) come numero decimale, ad esempio 3/4 = 3 : 4 = 0,75
c) come percentuale, ad esempio 0,75 = 75%
Nota. Per trasformare un rapporto in una percentuale si divide il numeratore per il denominatore e si moltiplica il risultato per 100.
In una serie di prove ripetute un gran numero di volte nelle stesse
condizioni, ciascuno degli eventi possibili si manifesta con una
frequenza relativa che è presso a poco uguale alla sua
probabilità. L'approssimazione cresce ordinariamente con il
numero delle prove.
(Guido Castelnuovo, Calcolo delle probabilità, Zanichelli)
frequenza relativa -> probabilità
Nota. La frequenza relativa di un evento è
il rapporto fra il numero di volte che si è verificato tale evento e il numero
totale delle prove fatte.
Si può esprimere come frazione, come numero decimale o come percentuale.
Esempio 1. Un un'urna ci sono palline bianche e palline
nere, ma non si sa quante sono. Estraendo una pallina, qual è la probabilità
che sia nera?
Per rispondere, dobbiamo dapprima fare molte prove, estraendo una pallina alla
volta e rimettendola nell'urna.
Supponiamo di aver fatto 85 prove e di aver estratto una pallina nera per 16
volte.
Si calcola quindi la frequenza relativa delle prove favorevoli, ottenendo così
un valore approssimato della probabilità.
frequenza relativa = 16/85 = 0,188 = 18,8%
dunque:
p(pallina nera) = 18,8% circa
Due eventi casuali A e B sono indipendenti se la probabilità di verificarsi dell'evento B non dipende dal fatto che l'evento A si sia verificato o no, e viceversa.
Esempio 1. Abbiamo due mazzi di carte da
40. Estraendo una carta da ciascun mazzo, i due eventi:
A = "La carta estratta dal primo mazzo è un asso"
B = "La carta estratta dal secondo mazzo è una carta di fiori"
sono indipendenti.
Un evento casuale B è dipendente da un altro evento A se la probabilità dell'evento B dipende dal fatto che l'evento A si sia verificato o meno.
Esempio 1. Abbiamo un mazzo di carte da
40. Estraendo due carte in successione, senza rimettere la prima carta estratta
nel mazzo, i due eventi:
A = "La prima carta estratta è un asso"
B = "La seconda carta estratta è un asso"
sono dipendenti. Per la precisione la probabilità di B dipende dal verificarsi
o meno di A.
Infatti:
a) la probabilità di A è 4/40
b) la probabilità di B, se la prima carta era un asso, è 3/39
c) la probabilità di B, se la prima carta non era un asso, è 4/39
Due eventi sono incompatibili se non possono verificarsi simultaneamente in una data prova.

Eventi incompatibili
Esempio 1. Estraendo una carta da un mazzo di 40, i due
eventi:
A = "Esce un asso"
B = "Esce una figura"
sono incompatibili.
Due eventi sono, invece, compatibili se c’è anche una sola possibilità che possano verificarsi simultaneamente, in una data prova.
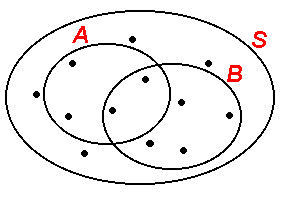
Eventi compatibili
Esempio 1. Estraendo una carta da un mazzo di 40, i due
eventi:
E1 = "Esce una figura"
E2 = "Esce una carta di cuori"
sono compatibili perché in una estrazione potrebbe uscire una figura di
cuori.
Siano A e B due eventi. Indichiamo con (A et B) l’evento che si verifica se e soltanto se si verificano sia A sia B.
Se i due eventi sono indipendenti, cioè il verificarsi dell’uno non influisce sulla probabilità dell’altro, la probabilità dell’evento (A et B) è uguale al prodotto delle probabilità di A e B:
p(A et B) = p(A) · p(B) (con A, B indipendenti)
Esempio 1. Abbiamo due mazzi di carte da 40. Estraendo una
carta da ciascun mazzo, consideriamo i due eventi indipendenti:
A = "La carta estratta dal primo mazzo è un asso"
B = "La carta estratta dal secondo mazzo è una carta di fiori"
Qual è la probabilità che si verifichino entrambi?
p(A) = 4/40
p(B) = 10/40
p(A et B) = 4/40 · 10/40 = 40/400 = 1/10
Se i due eventi sono dipendenti, cioè il verificarsi dell’uno influisce sulla probabilità dell’altro, si può applicare la stessa regola, purché con p(B) si intenda la probabilità di B nell’ipotesi che A si sia verificato.
p(A et B) = p(A) · p(B|A) (con A, B dipendenti)
Esempio 1. Un'urna contiene 2 palline bianche e 3 palline
rosse. Si estraggono due palline dall'urna in due estrazioni successive senza
reintrodurre la prima pallina estratta nell'urna.
Calcolare la probabilità che le due palline estratte siano entrambe bianche.
La probabilità che la prima pallina sia bianca è 2/5.
La probabilità che la seconda pallina sia bianca, a condizione che la prima
pallina sia bianca, è 1/4.
La probabilità di avere due palline bianche è:
p(due bianche) = 2/5 · 1/4 = 2/20 = 1/10
La probabilità che accada l'evento B, calcolata a condizione che l'evento A si sia verificato, si chiama probabilità condizionata o probabilità di B sotto la condizione A e si denota con p(B|A).
p(B|A) = p(A et B) / p(A)
Nota. Di solito la probabilità condizionata si applica
quando A dipende da B, cioè gli eventi sono dipendenti.
Nel caso in cui A e B sono indipendenti, la formula diventa p(B|A) =
p(B). Infatti il verificarsi o meno di A non condiziona la probabilità
p(B).
Esempio 1. Qual è la probabilità che estraendo 2 carte da
un mazzo di 40, la seconda sia di denari, nota l'informazione che la prima è
stata di denari?
p = (10-1)/39 = 9/39
oppure
p(denari | denari) = (10/40 · 9/39)/10/40 = 9/39
Siano A e B due eventi. Indichiamo con (A or B) l’evento che si verifica se e soltanto se si verifica A oppure B oppure entrambi.
Se i due eventi sono incompatibili, la probabilità dell'evento (A or B) è uguale alla somma delle probabilità di A e di B.
p(A or B) = p(A) + p(B) (con A, B incompatibili)
Osserviamo che se due eventi sono incompatibili non si possono verificare entrambi in una prova.
Esempio 1. Calcola la probabilità che estraendo una carta
da un mazzo da 40, sia un asso oppure una figura.
p(asso) = 4/40
p(figura) = 12/40
p(asso or figura) = 4/40 + 12/40 = 16/40 = 2/5
Se i due eventi sono compatibili, la probabilità dell'evento (A or B) è uguale alla somma delle probabilità di A e di B meno la probabilità che si verifichino entrambi.
p(A or B) = p(A) + p(B)- p(A et B) (con A, B compatibili)
Esempio 1. Un’urna contiene venti gettoni numerati da 1 a 20.
Calcola la probabilità dell’evento C = “Il gettone estratto ha
un numero multiplo di 2 oppure ha un numero multiplo di 5”.
Gli eventi "multiplo di 2" e "multiplo di 5" sono compatibili, infatti 10 e 20
sono multipli sia di 2 sia di 5.
p(multiplo di 2) = 10/20
p(multiplo di 5) = 4/20
p(multiplo di 2 e di 5) = 2/20
p(multiplo di 2 e di 5) = 10/20 + 4/20 - 2/20 = 12/20 = 3/5
Nota. Quando un evento si può verificare in più modi diversi e fra loro incompatibili, la sua probabilità è la somma delle probabilità corrispondenti a tali modi diversi.
Esempio 2. Lanciando due dadi, qual è la probabilità che la
somma dei numeri usciti sia 7?
Il totale 7 si può ottenere in 6 modi diversi e incompatibili (1+6, 2+5, 3+4,
4+3, 5+2, 6+1), ciascuno dei quali ha probabilità 1/36.
p(somma 7) = 1/36 + 1/36 + 1/36 + 1/36 + 1/36 + 1/36 = 6/36 =
1/6
Dato un evento A, si dice evento contrario di A l’evento che si verifica quando non si verifica A, ossia l’evento not A, complementare di A.
Due eventi contrari sono incompatibili.
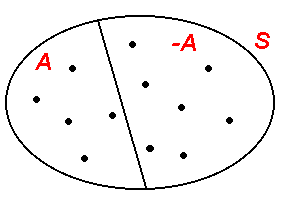
Eventi contrari
La probabilità di un evento si può ottenere sottraendo da 1 la probabilità del suo evento contrario.
p(A) = 1-p(not A)
Esempio 1.Trovare la probabilità che, lanciando due dadi,
si ottenga come somma delle facce un numero maggiore o uguale di 4.
Dato che un punteggio maggiore o uguale di quattro si può ottenere in molti
modi, conviene pensare l’evento come contrario di A = “si
ottiene un punteggio minore di quattro”. Gli eventi favorevoli
ad A sono le tre coppie (1, 1), (1, 2), (2, 1) per cui:
p(A) = 3/36 = 1/12
e la probabilità richiesta è:
p(not A ) = 1 - 1/12 = 11/12
Esempio 1. (tratto dai materiali didattici del prof.
Dario Palladino, Università di Genova - http://www.dif.unige.it/epi/hp/pal/dispense.htm)
Un’urna contiene 10 palline verdi e 7 palline rosse. Si estraggono
successivamente due palline, senza rimettere la prima nell’urna.
Qual è la probabilità che siano:
a) dello stesso colore;
b) di colore diverso;
c) almeno una rossa?
Per risolvere questo problema aiutiamoci con un diagramma ad albero: i quattro
rami rappresentano i possibili percorsi fra loro incompatibili e, in ciascun
tratto, è riportata la rispettiva probabilità.
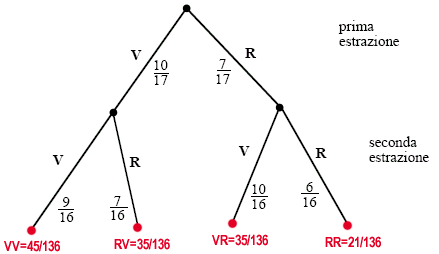
Ad esempio, considerato il ramo a sinistra (VV), nel primo
tratto figura la probabilità 10/17 che la prima pallina estratta sia verde, nel
secondo la probabilità 9/16 che la seconda pallina sia verde nell’ipotesi
che la prima sia verde (delle 16 palline ancora nell’urna, solo 9 sono
verdi).
Così, nel ramo RV, nel primo tratto figura la probabilità 7/17
che la prima pallina estratta sia rossa, nel secondo la probabilità 10/16 che
la seconda estratta sia verde nell’ipotesi che la prima pallina sia rossa
(tra le 16 palline rimaste vi sono tutte e 10 le palline verdi).
a) Per la regola della probabilità composta, la probabilità che entrambe le
palline siano verdi, ossia che si verifichi l’evento VV,
è 10/17 · 9/16 = 45/136.
Analogamente, la probabilità che entrambe le palline siano rosse, ossia che si
verifichi l’evento RR, risulta 7/17 · 6/16 = 21/136.
Quindi, la probabilità dell’evento “le palline sono dello stesso
colore”, ossia entrambe verdi o entrambe rosse, per la regola della
probabilità totale, è 45/136+21/136 = 66/136 = 33/68.
b) Per calcolare la probabilità dell’evento “le palline sono di
colore diverso”, anziché sommare la probabilità che la prima sia verde e
la seconda rossa con quella che la prima sia rossa e la seconda verde, possiamo
sfruttare quanto ottenuto in a) e applicare la regola della probabilità
dell’evento contrario; infatti l’evento “le palline sono di
colore diverso” è contrario di “le palline sono dello stesso
colore”, e quindi la sua probabilità è1-33/68 = 35/68.
c) La probabilità dell’evento “almeno una pallina è rossa” è
la somma delle probabilità dei tre eventi VR,
RV, RR. Più rapidamente si può calcolare la
probabilità dell’evento contrario a VV (“le
palline sono entrambe verdi”): 1-45/136 = 91/136.
Nota. La schematizzazione mediante grafi ad albero (associare ad ogni diramazione un evento e la relativa probabilità) si può usare quando gli eventi associati agli archi di una diramazione ("l'uscita è pari" e "l'uscita è dispari" nell'esempio dei dadi) costituiscono un gruppo completo di eventi (cioè almeno uno di essi deve accadere) incompatibili (nessuno di essi può accadere contemporaneamente ad un altro).
La speranza matematica (M) di una vincita (S) è il prodotto del valore che si spera di vincere per la probabilità di vincerlo (p(E)).
M = p(E) · S
Esempio 1. Un giocatore può vincere 72 EURO se, lanciando
due dadi, ottiene un doppio 6.
Qual è la sua speranza matematica?
E = "Escono due 6"
p(E) = 1/36
M = 72·1/36 = 2 EURO
La sua speranza matematica è di vincere 2 EURO.
Che cosa significa?
Se gioca una sola volta, o vince 0 EURO o vince 72 EURO. Ma se gioca molte
volte, la media che deve aspettarsi è di 2 EURO a giocata. Infatti,
statisticamente, vincerà una giocata ogni 36, cioè 35 volte 0 EURO e 1 volta 72
EURO.
La media è:
media = (35·0+1·72)/36 = 2 EURO
Nota. In questo caso, la speranza matematica è il valore medio di una variabile casuale (X) che può assumere soltanto due valori.
| Variabile casuale (X) | esce doppio 6 vincita = 72 |
non esce doppio 6 vincita = 0 |
| Probabilità (p) | 35/36 | 1/36 |
Più in generale, se S1, S2, …, Sn sono delle somme positive o negative (rispettivamente guadagni o perdite) la cui disponibilità è legata al verificarsi di n eventi che costituiscono una partizione dell’evento certo, si definisce speranza matematica (M) la somma dei prodotti delle Si per le rispettive probabilità:
M = S1·p1 + S2·p2 + … + Sn·pn
La speranza matematica, anche in questo caso, è il valore medio della variabile casuale.
Un gioco è equo se la speranza matematica è uguale a zero.
In molti (forse tutti?) i casi, il giocatore, per partecipare al gioco, deve pagare una posta (P). In questo caso, una definizione equivalente a quella precedente è:
Un gioco è equo se la posta (A) è uguale alla speranza matematica di vincita (M)
A = M
Il rapporto M/A permette di valutare l'equità del gioco.
Esempio 1. Alla roulette francese, il gioco "rosso e nero"
è equo?
Alla roulette ci sono 37 caselle, di cui 18 nere e 18 rosse.
Puntando sul rosso o sul nero, si incassa il doppio della posta.
Supponiamo di puntare 100 EURO sul rosso. E = "Esce rosso".
probabilità = p(E) = 18/37
posta: A = 100 EURO
vincita: S = 200 EURO
speranza matematica: M = 200·18/37 = 97,3 EURO
Per calcolare il "livello di equità" della roulette, si calcola il rapporto
M/A.
M/A = 97,3/100 = 0,973 -> 97,3%
Il gioco è evidentemente non equo, ma non troppo sbilanciato.
Esempio 2. Il gioco del lotto, puntando su un numero
singolo su una data ruota, è equo?
Supponiamo di puntare 100 EURO sul 25, ruota di Genova. E = "Esce il 25 sulla
ruota di Genova".
probabilità = p(E) = 5/90 = 1/18
posta: A = 100 EURO
vincita: S = (1123,2 - 100) = 1023,2 EURO (11,232 volte la posta meno la posta
stessa)
speranza matematica: M = 1023,2·1/18 = 56,84 EURO
Per calcolare il "livello di equità" dell lotto, puntando sull'Estratto, si
calcola il rapporto M/A.
M/A = 56,84/100 = 0,5684 -> 56,84%
Il banco del lotto vince mediamente poco più del 43% delle puntate, contro il
2,7% di quello della roulette.
Esempio 3. Se il lotto fosse equo, quanto si dovrebbe
vincere per aver indovinato un ambo su una data ruota?
probabilità ambo: p = 2/801
posta: A = 100 EURO
vincita lorda: 25000 EURO (250 volte la posta)
vincita netta: S = 24900 EURO (249 volte la posta)
| Variabile casuale (X) | esce ambo vincita = 24900 |
non esce ambo vincita = -100 |
| Probabilità (p) | 2/801 | 799/801 |
Speranza matematica, con la vincita realmente assegnata:
M = S1·p1 + S2·p2 = 24900·2/801 - 100·799/801 = -37,58 EUR
Continuando a giocare, si perde in media il 37,58% delle puntate
Se invece il gioco fosse equo:
probabilità ambo: p = 2/801
posta: A = 100 EURO
vincita netta: S = ?
A = S·p
100 = 2S/801
S = 80100/2 = 40050 EURO = 400,5 volte la posta.
Esempio 4. Il gioco dei 3 dadi.
Si tratta di un gioco assai diffuso nel medioevo. Su un grande tavolo è
disegnato un rettangolo diviso in 6 quadrati, numerati da 1 a 6.
Il banco invita gli spettatori a puntare su uno dei sei numeri.
Terminate le puntate, il banco getta tre dadi.
Chi ha puntato sul numero uscito in uno qualsiasi dei tre dadi vince il valore
della somma puntata.
Se il numero è presente su due dadi la vincita si raddoppia.
Se la "fortuna" fa uscire il numero su tutte e tre le facce, la vincita si
triplica.
Il gioco è equo?
>>>... da risolvere...
Esempio 5. Un gioco con un mazzo da 40 carte.
Il giocatore estrae una carta.
Se la carta è un asso, vince 30 EURO
Se è una figura, vince 12 EURO
In tutti gli altri casi deve pagare 14 EURO
Calcolare la speranza matematica del giocatore.
Il gioco è equo?
| Variabile casuale (X) | Asso +30 |
Figura +12 |
Né asso né figura -14 |
| Probabilità (p) | 4/40 | 12/40 | 24/40 |
La speranza matematica del giocatore è:
M = S1·p1 + S2·p2 + S3·p3 = 120/40 + 144/40 - 336/40 = -1,8
EURO
Il gioco non è equo e il giocatore, facendo tante partite, perde in media 1,8
EURO a partita.
Quando una persona è disposta a dare qualcosa in cambio di qualcos'altro che potrà o non potrà ottenere, con un certo intervento del caso, in realtà sta facendo un gioco d'azzardo.
Se continua a ripeterlo è perché crede che sia equo o meglio vantaggioso per sé.
Se in realtà il gioco è svantaggioso, evidentemente la persona ha valutato male i guadagni oppure le perdite oppure le probabilità.
Questo può aiutare a capire le valutazioni personali di un individuo.
Esempio 1.
| Variabile casuale (X) | Comportamento A vincita = A |
Comportamento B vincita = -B |
| Probabilità (p) | p | 1-p |
M = Ap - B(1-p) >= 0
A >= B(1-p)/p
Tratti dal sito Macosa (MAtematica per COnoscere e per SApere, Dipartimento di Matematica, Università di Genova) - http://macosa.dima.unige.it
Lancio del dado
Un dado (equo) viene lanciato due volte. Qual è la probabilità che il punteggio
ottenuto nel secondo lancio sia minore di quello ottenuto nel primo?
(A) 1/4 (B) 1/3 (C) 5/12 (D) 1/2 (E) 7/12
Sorteggio di una coppia
Una classe è formata da 13 femmine e 11 maschi. Vengono sorteggiati due alunni
per far parte della selezione degli alunni della scuola che parteciperà alla
festa organizzata in occasione della visita di una classe proveniente da un
altro paese. Qual è le probabilità che la coppia sorteggiata sia tutta
femminile? E quella che sia mista?
Tiro al bersaglio
Giorgio, al tiro al bersaglio, ha, statisticamente, una percentuale di successo
del 20% (ossia la frequenza con cui centra il bersaglio è del 20%). Se non
dispongo di altre informazioni, di fronte alla effettuazione di cinque tiri da
parte di Giorgio, devo ritenere più probabile (1) che non colpisca mai il
bersaglio, (2) che lo colpisca una sola volta o (3) che lo colpisca più di una
volta?
A) i primi due eventi hanno la stessa probabilità, inferiore alla probabilità
del terzo
B) i primi due eventi hanno la stessa probabilità, superiore alla probabilità
del terzo
C) il primo evento è più probabile degli altri
D) il secondo evento è più probabile degli altri
E) il terzo evento è più probabile degli altri due, che hanno tra loro
probabilità diverse
Pezzi difettosi
In una fabbrica che produce un particolare componente per computer alla fine
del ciclo produttivo viene effettuato un controllo "a vista" che mediamente
indivua ed elimina l'80% dei pezzi difettosi ma, erroneamente, elimina anche il
7% dei pezzi non difettosi. Supponiamo che si sappia che, in media, i pezzi
difettosi prodotti sono il 10%. Qual è la probabilità che un pezzo che supera
l'esame sia difettoso?
Test sanitario
Un certo test sanitario per valutare la presenza (esito positivo) o assenza
(esito negativo) della malattia X ha attendibilità del 95% (in caso di presenza
c'è il 95% di probabilità che l'esito sia positivo , in caso di assenza il 95%
di probabilità che sia negativo). Si sa da statistiche serie che l'1% della
popolazione è affetta dalla malattia X. Se per una persona il test dà esito
positivo, qual è la probabilità che essa sia realmente malata?
Dipendenza indipendenza
Lancio un dado equo. Siano X l'evento "esce un numero pari", Y l'evento "esce 1
o 4" e Z l'evento "esce un numero minore o eguale a 3". Quale delle seguenti
affermazioni è vera?
(A) X e Y sono entrambi indipendenti da Z
(B) X è indipendente da Z e Y non lo è
(C) Y è indipendente da Z e X non lo è
(D) X e Y sono entrambi dipendenti da Z
(E) Non ho informazioni sufficienti per stabilire quali tra le precedenti
affermazioni è vera
Lancio del dado
5/12
Sorteggio di una coppia
Si può fare un grafo ad albero.
p(coppia femminile - FF) = 13/46
p(coppia mista - MF or FM) = 143/276
Tiro al bersaglio
p(che non colpisca mai il bersaglio) = 0,84
p(che lo colpisca una sola volta) = (0,2*0,8*0,8*0,8*0,8)*5 =
0,84
p(che lo colpisca più di una volta), è l'evento complementare dei primi due, =1
- (0,85+0,84)
Pezzi difettosi
Si può fare un grafo ad albero: inizio - difettoso/buono - preso/scartato.
Ogni 100 pezzi, quelli che superano l'esame mediamente sono 85,7, quelli tra
questi difettosi sono 2. La frequenza con cui tra i pezzi che superano ve n'è
uno difettoso è 2/85,7 = 2,3%. Questa è la probabilità cercata.
In altri termini:
p(EssereDifettoso | EsserePreso) =
= p(EssereDifettoso & EsserePreso) / p(EsserePreso) =
= 2/85,7 = 2,3%
Test sanitario
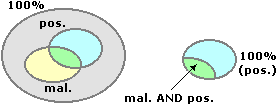
Si deve calcolare la probabilità condizionata di essere malato sotto la
condizione di essere positivo:
p("essere malato" | "risultare positivo") =
= p("essere malato" et "risultare positivo") / p("risultare positivo") =
= 0,95% / 5,90% = 16%
Per calcolare p("risultare positivo") si può fare un diagramma ad albero:
inizio - malato/non malato - positivo/negativo.

Questo esempio evidenzia il ruolo del calcolo delle probabilità nella
razionalizzazione delle situazioni "incerte".
Esso non è tuttavia sempre sufficiente. Si pensi ai vaccini,
che a volte hanno una certa probabilità di causare l'insorgere delle malattie
stesse; per decidere se rendere obbligatoria una vaccinazione non basta trovare
che tale probabilità è bassa rispetto alla diffusione della malattia: imporre a
chi potrebbe rimanere sano una vaccinazione che può causare una malattia
comporta valutazioni anche di tipo morale.
Dipendenza indipendenza
Y è indipendente da Z e X non lo è.
Data creazione: maggio 2008
Ultimo aggiornamento: gennaio 2013
xhtml 1.1
Sito Web realizzato da Gianfranco Bo