Ricreazioni Febbraio 2002

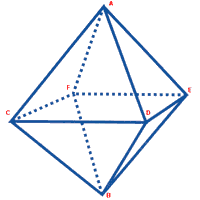
204. Dipingere gli spigoli di un ottaedro
di Peppe
Si vogliono dipingere gli spigoli di un ottaedro senza mai staccare il pennello e senza ripassare sulla vernice già data.

>>> Risposte & riflessioni
Peppe
N.B. Nella soluzione di Peppe l'ordine delle lettere è diverso.
Possiamo immaginare l'ottaedro come un grafo nello spazio: i vertici sono i nodi, gli spigoli sono gli archi.
La rete di collegamenti può essere schematizzata nel piano da un grafo equivalente.
Ciascun nodo ha grado pari, perciò esiste un percorso chiuso che passa per tutti gli archi.
Nell'ordine il percorso passa per questi vertici: D, A, C, B, A, E, B, F, C, D, F, E, D.

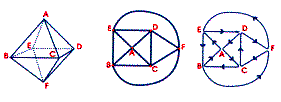
Ivana
Si dipingono nell'ordine i seguenti spigoli (spero di aver letto bene le lettere che compaiono nella rappresentazione grafica!):
CB; BD; DA; AC; CD; DE; EF; FB; BE; EA; AF; FC.
Logicamente è valido anche il percorso a ritroso: CF; FA; AE; EB; BF; FE; ED; DC; CA; AD; DB; BC.
Sono convinta che ci siano altri percorsi possibili...

203. Le due navi
di Ivan Furlan
(N.B. questa ricreazione mi è stata inviata nell'ottobre del 2001)
Una nave che si muove alla velocità V1 in direzione est, incrocia proprio davanti a sè, distante d un'altra nave che si muove in direzione nord alla velocità V2.
La nave1 comincia a seguire la nave2 puntandola sempre.

Domande:

1) Se V1=V2, dopo molto tempo quado le due navi si muovono un in fila l'altra verso nord, a che distanza si trovano le due?

2) Se V1>V2, dopo quanto tempo la nave1 raggiunge la nave2?

>>> Risposte & riflessioni
Attenzione:
integrale{sin(alfa)*dt}_0_t : intendo integrale da 0 a t della funzione sin(alfa)
alfa = angolo della nave1 tra rotta istantanea e rotta iniziale.

La distanza in direzione nord tra le due navi al tempo t è:

Snord = V2*t - V1*integrale{sin(alfa)*dt}_0_t

La distanza che la nave1 vede tra sè e la nave2 al tempo t è:

S = d - V1*t + V2*integrale{sin(alfa)*dt}_0_t

Risposta 1)

Siccome al momento t infinito tra le due navi
la distanza nord sarà costante, mentre l'altra distanza sarà 0:

x = V*t - V*integrale{sin(alfa)*dt}_0_t
0 = d - V*t + V*integrale{sin(alfa)*dt}_0_t
(le due equazioni sono da considerare due limiti tendenti all'infinito)

eliminado l'integrale dalle due equazioni, ottengo:

x= V^2*t - V*(V*t-d)
x=d

Dunque al tempo t tendente all'infinito la distanza nord tra le navi sarà x.

Risposta 2)

Siccome al momento dell'incontro tra le navi, le due distanze saranno 0, posso
scrivere:

0 = V2*t - V1*integrale{sin(alfa)*dt}_0_t
0 = d -V1*t + V2*integrale{sin(alfa)*dt}_0_t

eliminado l'integrale dalle due equazioni, ottengo:

0= V2^2*t - V1*(V1*t-d)

che risolta rispetto a t dà:

t= d*V1/(V1^2-V2^2)
che è il tempo d'incontro.

202. I "taxi-percorsi"
di Ivana Niccolai e Dino
Siamo negli Stati Uniti d'America, precisamente a Manhattan, cuore di New York City, dove, si sa, le strade sono tutte squadrate suddivise in Street ed Avenue che si intersecano tra loro a formare angoli retti e dove tutti gli isolati presentano le stesse identiche dimensioni planimetriche. Se si interpreta questo reticolato su un piano, gli incroci tra le strade possono essere visti quali "punti" d'intersezione tra le "rette" che costituiscono perciò i percorsi possibili tra due isolati lungo le strade.

I tassisti di questa città sono dei gran furbacchioni: se un cliente deve andare da un punto A ad uno B cercano di fare non il percorso più breve, ma un percorso alternativo, più lungo. Poiché i turisti protestarono per la perdita in termini economici e di tempo, il Sindaco emise un'ordinanza nella quale veniva esplicitato che se un tassista continuava ad imbrogliare un turista, facendogli fare un percorso più lungo del dovuto, gli veniva ritirata la licenza e confiscata l'auto.

Ecco allora che i tassisti di New York City divennero tutti onesti, ma per non annoiarsi organizzarono tra loro un gioco: ogni volta che un passante o un turista chiedeva di andare da A a B, due nodi del reticolato, ogni tassista doveva cambiare percorso, scelto solo tra quelli possibili, di lunghezza minima.

Ma come fare a sapere quanti sono percorsi del genere una volta assegnati due nodi A e B?

>>> Risposte & riflessioni
Enrico Delfini
E così avete scoperto il Rettangolo di Tartaglia!
Considerando (m;n) le coordinate del punto d'arrivo, si comprende come ci sono due possibili "penultimi punti" (m-1;n e m;n-1), per cui il numero dei possibili percorsi terminanti in (m;n) è la somma dei due risultati "penultimi": già questa ricorsività indirizza verso un risultato tartagliesco.
Per trovare il nodo del triangolo che dà la soluzione, si può seguire la m-esima diagonale, fermandosi all'n-esimo posto, oppure si può leggere il triangolo stesso in righe orizzontali classiche in cui la riga (m+n)-esima contiene i risultati per ogni possibile coppia di m;n che danno la stessa somma (es.: la nona riga riporta i risultati per 0;9 - 1;8 - 2;7 - 3;6 ecc...)
Esiste una complicazione: Le avenues di Manhattan hanno tutte il senso unico, verso nord quelle col numero pari, verso sud quelle dispari, con l'eccezione di Park Av. che ha doppio senso di marcia. Questo per precisinismo ;-)

Dino e Ivana Niccolai
Nell'inviarti il file soluzione (dove puoi trovare altre considerazioni interessanti) facciamo innanzitutto i nostri complimenti a Enrico per la risposta immediata e corretta e di precisiamo anche che non si è tenuto conto dei sensi unici (che lui ha fatto notare e noi sapevamo già) per generalizzare quanto più il problema ad una qualsiasi città-rettangolo.

Cominciamo ad immaginare il centro di Manhattan come città-rettangolo, e stabiliamo che l'unità di misura per la lunghezza dei percorsi sia l'isolato singolo, ovvero che le dimensioni dei lati planimetrici di questi siano unitari. Un taxi deve quindi seguire il minimo tragitto fra due punti qualsiasi, A e B, come nella figura seguente.

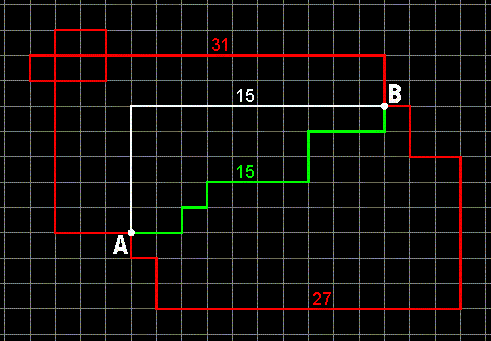
In figura sono stati riprodotti più percorsi alternativi: in bianco quello minimo più logico della lunghezza pari a 15; ma anche quello verde, più articolato, va bene allo scopo in quanto la somma dei vari rettifili è sempre pari a 15; in rosso, invece, sono stati riprodotti due possibili percorsi "disonesti" e quindi più lunghi di quasi il doppio di quelli minimi consentiti (in un caso si raggiunge la lunghezza 27, nell'altro addirittura 31). Consideriamo ora un sistema di assi cartesiani, x ed y, con l'origine posto, per semplicità, nell'angolo in basso a sinistra della nostra città-rettangolo. Nel sistema suddetto le coordinate cartesiane del punto A siano x_A ed y_A, mentre del punto B x_B ed y_B. Nella figura precedente si è supposto che x_B ed y_B siano rispettivamente maggiori od uguali di x_A ed y_A, ma qualora tali condizioni non fossero rispettate basta scambiare i due punti fra loro o considerarne il simmetrico di B rispetto all'asse cartesiano del caso: in questo modo non verrà a mutare la distanza reciproca fra i punti di partenza ed arrivo e quindi neanche il numero dei percorsi leciti consentiti dai taxi. Ponendo però l'origine del sistema di riferimento, x' ed y', proprio nel punto A si hanno le seguenti coordinate relative:

Il percorso bianco della figura precedente mostra eloquentemente che le coordinate relative di B, rispetto ad A, sono indicative della distanza d minima richiesta dal taxi in quanto risulterà sempre:

Ma quanti sono questi taxi-percorsi consentiti? Consideriamo come prima cosa una posizione banale di B in cui si verifica che una delle due sue coordinate relative rispetto ad A sia nulla. Ciò evidentemente si verifica quando è x_B = x_A oppure y_B = y_A: in tal caso la risposta è facile, come si vede nella figura successiva, dato che il numero dei percorsi possibili è sempre unico dovendo il taxi seguire l'unico rettifilo possibile coincidente con uno dei due assi cartesiani presi nel sistema di riferimento relativo.

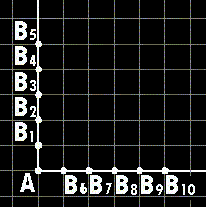
Passiamo al caso in cui le due coordinate relative di B rispetto ad A risultano entrambe non nulle e andiamo a calcolarci, per i vari punti più vicini ad A, il numero di percorsi alternativi che possono aversi rispettando sempre la condizione che essi siano i più brevi possibili. Ruotando in modo opportuno la città-rettangolo e portando il punto A in alto si hanno i seguenti risultati in cui in ogni incrocio è riportato il numero dei relativi tragitti consentiti:

Considerando il solo triangolo numerico così ottenuto ci si rende subito conto che siamo di fronte al ben noto triangolo di Tartaglia col vertice (riga zero) decapitato, per cui gli m possibili traggitti leciti che possono effettuare i taxi sono ricavabili facilmente col binomio di Newton ponendo n = d e k = y_B', vale a dire sostituendo:

Facciamo un esempio possibile: poniamo che un taxi debba compiere il tragitto dal punto di coordinate x_A = 3 ed y_A = 16 al punto x_B = 14 ed y_B = 7; trasferendo l'origine del sistema di assi cartesiani nel punto A si ricavano le coordinate relative:

Volutamente si è preso il punto B tale le sue coordinate relative cadessero nel secondo quadrante (la y_B' risulta negativa), ma il simmetrico rispetto all'asse x' (positivo) non muta la distanza e il numero di percorsi leciti da A perciò faremo riferimento al punto di coordinate x_B' = 11 e y_B' = 9 sicuri di ottenere gli stessi risultati. Per quanto detto la distanza minima che deve compiere il taxi dev'essere pari a:

Francesco Veneziano
Chiamiamo x e y le distanze in orizzontale ed in verticale che separano A e B, ed f(x,y) il numero di percorsi diversi.
Per il primo tratto di strada, il taxi può andare in verticale, nel qual caso gli rimangono ancora f(x-1,y) strade possibili, o in orizzontale, nel qual caso gli rimangono f(x,y-1) strade possibili.
Quindi f(x,y)=f(x-1,y)+f(x,y-1) e naturalmente f(x,y)=f(y,x).
Ponendo f(x,y)=C(x+y,y) e sostituendo nella relazione otteniamo la celebre relazione di ricorrenza per i coefficienti binomiali, quindi il numero di percorsi diversi è C(x+y,y)=C(x+y,x)

Problema geometrico e soluzione ideata da due giovani studenti americani.
Due studenti hanno risolto un problema meglio di quanto fece il grande studioso greco.
Capelli ben pettinati, guance rosee, enormi occhiali, l'apparecchio per i denti: David Goldenheim e Daniel Lichtfield, due giovani americani, non sono proprio il tipo di studenti che le ragazze applaudono durante le partite di baseball del college.
Eppure, da quando la rivista specializzata Mathematics Teacher ha pubblicato una loro scoperta di geometria, sono diventati delle celebrità non solo alla Green farms academy, nel Connecticut, dove frequentano l'equivalente della nostra prima classe del liceo scientifico, ma fra i matematici di mezzo mondo.
Tutto è cominciato un paio di mesi fa, quando Charles Dietrich, l'insegnante di matematica, ha deciso di assegnare ai due questo problema: dividere un segmento in parti uguali usando solo la riga e il compasso.
La soluzione, ha spiegato Dietrich, è stata trovata 2.300 anni fa dal grande Euclide nei suoi Elementi, con un insieme di cerchi, triangoli e parallele. A David e Daniel sono bastate un paio d'ore per sciogliere l' enigma. «Quando ho visto come avevano fatto» ricorda Dietrich «mi è quasi venuto un infarto». I due ragazzi, infatti, avevano trovato una soluzione diversa da quella di Euclide, assai più semplice ed "elegante". E senza neppure sfiorare una riga o un compasso, ma usando un programma grafico per computer.
Curiosamente, nel corso della dimostrazione hanno anche trovato uno stretto rapporto fra la loro soluzione e la sequenza di Fibonacci, una serie numerica in cui ogni numero è la somma dei due che lo precedono.
E ora David e Daniel, che hanno battezzato la loro soluzione GLaD dalle iniziali dei rispettivi cognomi, si godono il meritato momento di gloria. Gli inviti a seminari e convegni per raccontare la soluzione escogitata si sprecano, e in Aprile i due amici saranno a Minneapolis, come ospiti d'onore all'incontro annuale del Council of teacher of Mathematics americano.
Tratto da Panorama 20/3/97 n° 161

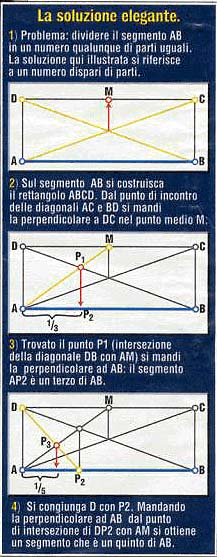>>> Risposte & riflessioni
Gianfranco Bo
La soluzione è molto interessante.
Ad una prima lettura mi sono chiesto: "Com'é possibile costruire un rettangolo su un dato segmento e tracciare delle perpendicolari senza l'aiuto di un compasso?
In effetti questa costruzione richiede di tracciare un rettangolo, congiungere coppie di punti e di tracciare linee verticali (piuttosto che perpendicolari). Ciò è possibile anche con i più elementari programmi di grafica (tipo Paint) poiché il rettangolo è una delle figure precostituite e le linee verticali si riconoscono in quanto non hanno "scalini".

Enrico Delfini
Con tutto il rispetto e la simpatia per i due ragazzi americani, mi permetto di trovare un po' eccessivo l'entusiasmo. La regola di "usare solo riga e compasso", non è una regola cervellotica, ma corrisponde all'uso degli strumenti minimi e non "discreti". Mi sembra che usare il computer, con un sofisticato programma di grafica, sia interessante, ma non credo che possa essere considerato meno tecnologico di una riga "non numerata" e di un pezzo di spago (= compasso).
Sarebbe come dire che ho trovato il modo di fare le radici quadrate senza calcoli, perchè uso una calcolatrice.
Il sistema è peraltro davvero ingegnoso, ed è molto simile al procedimento che si usava alle medie per "squadrare" i fogli di disegno per la professoressa Gibertoni, che pretendeva il solo uso del compasso, senza riga.

"Un marziano di nome Floyd riuscì a contattarti casualmente tramite il tuo televisore nel corso di un programma incentrato sugli alieni.
La trasmissione stava appena dicendo che i marziani hanno capacità matematiche inferiori a noi terrestri quando improvvisamente Floyd comparve sullo schermo smentendo tutto quello che si stava sostenendo sulla loro specie compreso il numero delle dita delle loro tre mani dichiarate in apertura di programma.

Dopo aver vinto le paure e le sorprese di ciò che ti stava capitando riuscisti a riprendere il controllo della situazione ed a chiedere prontamente a Floyd: "Perchè, fammi vedere una tua mano, quante dita ci sono?"

"Troppo bello! ... " rispose il marziano " ... Telefona subito in trasmissione e dì che Floyd afferma che le dita di ogni mano di noi marziani è tale che la differenza delle radici dell'equazione:

x² - 16·x + 41 = 0

è pari a dieci!"

Floyd scomparve poco dopo non fornendo ulteriori chiarimenti sull'enigma. A quel punto davvero non capivi più nulla e formulasti il numero dell'emittente televisiva per raccontare in diretta l'accaduto, ma con maggiore sorpresa ti accorgesti che il conduttore riuscì subito a svelare il mistero ...

Quante dita, secondo Floyd, hanno i marziani in ogni mano?"

>>> Risposte & riflessioni
Francesco Veneziano
Non conosco l'autore della storia, ma il problema ha fatto parte dello scritto di ammissione alla Normale di Pisa degli anni passati.

Andro
8 dita.
i numeri coinvolti nel problema (16, 41 e 10) se letti in base 8 corrispondono ai numeri in base 10 (14, 33 e 8).
Le soluzioni dell'equazione sono 3 e 11.
Ho ragionato così:
l'equazione di secondo grado in questione è di quelle che, se si cercano soluzioni intere, si possono leggere anche così: trovare 2 numeri tali che la loro somma sia uguale al coefficiente del termine di primo grado (16) e il loro prodotto al termine noto (41).
Partiamo dal prodotto. 41 è primo, dunque è dato da 1 * 41. La differenza è 40 e deve essere 10.
Cambiamo base e proviamo a scendere.
In base 9 il prodotto è 37, anch'esso primo. Nulla da fare.
Scendiamo ancora.
In base 8 il prodotto è 33, che è dato anche da 3 * 11. Mi sa che ci siamo. Si controllano a questo punto la somma che è 14 (16 in base 8) e la differenza che è 8 (10 scritto in base 8).

Dino
Il tuo ragionamento non fa una piega! La base da cercare però poteva anche essere > di 10 ed in tal caso avresti dovuto fare ulteriori tentativi ...
A tuo beneficio, e a quello degli altri, scrivo la soluzione analitica rigorosa:
In effetti il gioco stava nel capire che il numero delle dita di una mano del marziano equivale alla base del suo sistema di numerazione, perciò si trattava di dover individuare, dai dati forniti, qual'è questa base B esprimendo con la quale i numeri si riesce a fare tornare tutti i conti. Inannzitutto possiamo dire che si tratta di una base maggiore di sei visto che tale cifra compare nell'equazione.

Se le radici di un'equzione qualsiasi sono a e b e il coefficiente di x² dell'equazione è unitario, l'equazione stessa può essere riscritta anche in quest'altro modo:

(x - a)·(x - b) = 0

cioè:

x² - (a + b)·x + a·b = 0

ovvero si ha che il coefficiente di x è uguale alla somma delle radici cambiata di segno e il termine noto è il prodotto delle due radici. A questo punto, visto che conosciamo i coefficienti dell'equazione possiamo scrivere, denotando con B la base di numerazione del marziano espressa nel nostro sistema decimale, e supponendo che a sia maggiore di b:

a - b = (10) in base B = (B) in base 10

a + b = (16)in base B = (B + 6) in base 10

a·b = (41) in base B = (4·B + 1) in base 10

ricavando il valore di a dalla prima e sostituendolo nella seconda otteniamo:

b = (3) in base 10

e quindi per la prima:

a = (B + 3) in base 10

Sostituendo così il tutto nella terza si ha:

a·b = [3·(B + 3)] in base 10 = (4·B + 1) in base 10

da cui ricaviamo B = 8 ovvero il sistema numerico dei marziani è in base otto od ottale e le tre mani dei marziani hanno otto dita caduna. Possiamo verificare anche che riscrivendo tutto in base decimale si ha:

x² - 14·x + 33 = 0

che ha come radici appunto 3 ed 11.

Archimede
Io l'ho risolto con la formula risolutiva delle equazioni di secondo ordine:

Lavorado in base 10:
x1,2 = ((B+6) + - ((B+6)^2-4*(4*B+1))^0.5)/2

quindi: x1 - x2 = ((B+6)^2-4*(4*B+1))^0.5 = B
(B+6)^2-4*(4*B+1)=B^2
12B+36-16B-4=0
4B=32
B=8

Recentemente ho ricevuto un messaggio cifrato da alcuni alieni con cui mi sono sintonizzato tempo fa tramite il progetto SETI (ma non l'ho ancora detto a nessuno).
Siamo riusciti a stabilire un codice e hanno anche imparato i numeri arabi.
Ho detto loro che mi collego col sito di Base Cinque via internet e ho detto che sul sito vi sono 352 mesaggi.
Grazie alla loro tecnologia, hanno fatto altrettanto e mi hanno risposto (delusi credo) che loro ne contavano 140.
Come è possibile secondo voi, tenendo conto che 352 sono tutti i messaggi (ovviamente è un numero fittizio) e non si può dire che ve ne sono di meno o di più?

>>> Risposte & riflessioni
Dino
Gli alieni adottano un sistema numerico non decimale.

Andro
Sì, ma quale?
In base 16, 140 corrisponde a 320 decimale, mentre in base 17, 140 corrisponde a 357.

Damiano
Non capisco questo razzismo ;-)
Perchè dovrebbero essere gli alieni a non usare il sistema decimale ?
E non invece il caro Giovanni... ma non voglio rovinarvi il piacere.

Ivana
Damiano ha ragione:
352 (base 6 ) corrisponde proprio a 140 (base 10)

Per Damiano
Non mi sembra, forse, adeguato il termine "razzismo"; credo vada sottolineata, piuttosto, l'abitudine di noi occidentali all'etnocentrismo culturale.

Giovanni Macchia
Allora, non ve ne abbiate a male se ieri sera non vi ho risposto: non mi collego ad Internet di sera a causa di tanti impegni.
In effetti, gli alieni hanno 6 dita e quindi contano in base 6.
Bravi tutti!!!

Questa ve la devo raccontare prima che mi cada di mente.
Forse per qulacuno e' una cosa nota. Per me e' un'interessante "scoperta".
Poco fa ho riaperto il congelatore, dopo piu' di 15 giorni di assenza da casa (sono stato dai miei in Calabria per le feste).
Dovevo prendere una cosa.
A prima vista sembrava tutto a posto: ho trovato tutte le cose ben congelate al loro posto. Ma ... ho notato una cosa che mi fa essere matematicamente anzi fisicamente certo che c'e' stato un black out e anche lungo.

Cosa ho notato?

Oppure, detto in altri termini, immaginate di progettare un termometro storico che "registri" dei lunghi black out, cosa fate?

>>> Risposte & riflessioni
Paolo P.
Qualche anno fa è successo anche a me.
I ghiaccioli, che in origine erano belli cilindrici e avvolti attorno allo stecchino, erano piatti e informi.
E' quello che hai visto tu?

Enrico Delfini
Appure una giovane anguilla congelata dritta e riposta in diagonale che hai ritrovato piegata ad angolo retto.

Sprmnt21
Infatti proprio questo ho notato. Non l'anguilla ma una vaschetta di gelato che avevo cominciato a consumare "scavando in verticale" partendo da un lato della vaschetta. Ieri mi sono accorto che il gelato riempiva uniformrnte tutta la base della vaschetta: l'ho buttato :-((.

Vediamo scoppiare un fuoco artificiale ad una certa distanza da noi. Misuriamo quindi il tempo che impiega il suono a giungere alle nostre orecchie.
Quale calcolo dobbiamo effettuare per ottenere in modo teoricamente impeccabile la distanza tra noi e l'esplosione.

>>> Risposte & riflessioni
Andro
In modo approssimato, si suppone che la luce si propaghi istantaneamente e il tempo misurato dalla vista del fuoco all'udito dello scoppio va moltiplicato per la velocità del suono (340 m/s) e si ottiene lo spazio percorso.

In modo impeccabile, si potrebbe procedere così.
Indichiamo con
Vl=velocità della luce (299.972 Km/s)
tl=tempo impiegato dalla luce a percorrere la distanza S
Vs=velocità del suono (340 m/s)
ts=tempo impiegato dal suono a percorrere la distanza S

S=Vl*tl
S=Vs*ts

In questo caso il tempo t da noi misurato è t=ts-tl da cui ts=t+tl

Combinando le prime 2 eguaglianze e la terza otteniamo
Vl*tl=Vs*(t+tl)
Ricavando tl abbiamo
tl=Vs*t/(Vl-Vs)
Da cui si può calcolare S.

Scomponendo in fattori:
(z-1)(1+z+z^2+z^3+z^4)=0
e poichè z<>1 risulta

1+z+z^2+z^3+z^4=0

Quindi:
p(z)=(1-z)(1-z^4)*(1-z^2)(1-z^3)=
(1-z-z^4+z^5)*(1-z^2-z^3+z^5)=
(2-z-z^4)(2-z^2-z^3)=
4-2z^2-2z^3-2z+z^3+z^4-2z^4+z^6+z^7=

Sprmnt21
Eccola qua! quella di Damiano e' una delle (due) prove che ho trovato anch'io. Ce n'e' un'altra (ma praticamente equivalente, solo che "gioca" in modo diverso con le ipotesi) che magari, se qualcuno non la scrive prima, scrivero piu' in la'.
In questo caso, volevo solo fare delle osservazioni sul problema.

Nonostante abbia trovato la soluzione "semplice" non sono soddisfatto. Nel senso che non riesco a "penetrare" bene la questione e a capire cosa c'e' veramente dietro.

Io sono (sentimentalmente) certo che il risultato trovato ha una portata piu' generale, ma il metodo per arrivare a questa soluzione non mi permette di capire la cosa fino in fondo.
Faccio un esempio per cercare di chiarire cosa intendo. Ho fatto un po' di "esprimenti numerici" provando a vedere se il risultato valesse anche per n>5. Ho provato a passare da p(z)=(1-z)(1-z^2)(1-z^3)(1-z^4) a p(z)=(1-z)...(1-z^8) cioe n=9 ma non funziona. Invece provando per n=17 la cosa vabbene. Allora la mia congettura e' che la cosa "funzioni"
per quegli n=2^k+1 che sono primi.
Il risultato per n=17 l'ho ottenuto allo stesso modo che per n=5. Il limite del metodo e' proprio qua se volessimo provare la congettura avremmo bisogno di un metodo diverso non possiamo esplicitare espressioni per, chesso', n=129 e cosi via.
Qua sembrano entrarci quelle proprieta' dei poligoni regolari "costruibili" con riga e compasso, ma chissa come'?

Una seconda osservazione che volevo fare e' la seguente. Proprio dalla soluzione tipo quella che ha illustrato Damiano deriva questa simpatica proprieta':

Se z=/=1 e z^5=1 allora

(1-z)*(1-z^2)*(1-z^3)*(1-z^4)=(1-z)+(1-z^2)+(1-z^3)+(1-z^4)

La stessa cosa vale z=/=1, z^17=1.

195. Il delitto della stanza chiusa
di Paolo P.
Un uomo viene trovato morto in una stanza. La porta e le finestre sono chiuse dall'interno.
Il medico legale vede subito che la causa della morte è una ferita da arma da fuoco, ma all'interno della stanza non viene trovata nessuna arma.
Come si spiega ?

G. Macchia
L'uomo è morto per dissanguamento a causa di una ferita di arma da fuoco. Prima di morire ha avuto il tempo di gettare la pistola, chiudere le finestre e la porta e aspettare di morire dissanguato.
Elementare, mio caro Watson...

Paolo P.
Andro :Botole? Passagi segreti? Lucernari? Niente di tutto ciò.
GM : perchè l' uomo avrebbe dovuto buttare la pistola, chiudere tutto e lasciarsi morire, invece di cercare aiuto ?

Enrico Delfini
La ferita risale a un certo tempo prima, e ha causato la morte non in modo istantaneo; il malcapitato nel tempo intercorso fra la ferita e la morte era ingrado di muoversi normalmente, o quasi. Ha pertanto chiuso lui porte e finestre.

Altra soluzione: Le finestre sono chiuse, ma mancano i vetri.

Paolo P.
Colpa mia, l'ho fatta troppo facile. Forse invece di parlare di ferita, dovevo dire che l' uomo era morto per un "colpo" di arma da fuoco.
Enrico: tra lo sparo e la morte sono passati solo pochi secondi e in questo tempo l'uomo non poteva muoversi "normalmente".
Fate l'ultimo facilissimo passaggio che manca e ricostruite l'accaduto. Dov'è l'arma ?

Enrico Delfini
Il testo non dice che l'arma non è nella stanza, ma che non viene trovata, quindi... l'ha ingoiata il cane pastore maremmano, accucciato sornione ai piedi della vittima.
L'aveva ingoiata il morto, e lo sparo è partito dall'interno dello stomaco.
E' stata sollevata lungo la cappa del camino legata con uno spago ad un pallone sonda.
Il medico legale aveva alzato il gomito ed ha sbagliato diagnosi.

CFB
L'uomo si è sparato con una pistola a forma di biro. La scientifica non l'ha esaminata bene notando che la penna non scriveva.....

Andro
Gli hanno sparato dalla finestra, che è chiusa, ma ha un foro di proiettile nel vetro.

Paolo P.
A cfb e Andro
L'uomo si è sparato con una pistola a forma di biro: NO
Gli hanno sparato dalla finestra: NO

Paolo P.
No, dovrebbe esserci anche la pistola.
Non vorrei avervi sviato. Enrico Delfini ha posto la questione essenziale: l' uomo non è morto SUBITO, ma le finestre erano GIA' chiuse dall' interno quando l' uomo è entrato. Più chiaro?

Enrico Delfini
E' stato ucciso a bordo di una mongolfiera ed è caduto entrando per la cappa del camino

CFB
ok!
L'uomo è stato sparato, inseguito si è rifugiato in una stanza ha chiuso a chiave per evitare che l'assasino lo insegua ma non è riuscito a fare nient'altro....

Andro
Allora gli hanno sparato dalla porta e poi dall'esterno l'hanno chiusa con una calamita (non so se si può fare davvero, ma forse in teoria sì).

Paolo P.
BRAVISSIMI!
Giusta quella di cfb.
Ce l' aveva quasi fatta a chiudersi dentro, ma l' assassino gli ha sparato dall'ultimo spiraglio. La vittima ha avuto solo il tempo di girare la chiave.

Io dico che il 9 e il 28 sono entrambi, potenzialmente, due numeri palindromi uguali.
In base a quale ragionamento posso sostenere una simile affermazione?

>>> Risposte & riflessioni
Roberto
Forse pensi alla loro scrittura in formato digitale?

Ivana Niccolai
Bravissimi entrambi!
Enrico ha spaziato con la sua...creatività!
Esattamente
9 = 1001 in base 2
28 = 1001 in base 3

Molto tempo fa, cercando di stabilire la relazione tra due grandezze tratte, se così si può dire, dalla vita di tutti i giorni, ottenni la seguente semplice formula:

y=100(1-100/(100+x))

Sapreste individuare a che cosa potrebbero corrispondere x e y ?
(N.B. Non ho la minima idea del grado di difficoltà di questo problema)

>>> Risposte & riflessioni
Enrico Delfini
Se il tuo vicino ha un podere di area 100, e il tuo podere è di area x, qual è la probabilità che un meteorite cada sul tuo piuttosto che sul campo del vicino.
Dipende da cosa intendi per "nella vita di tutti i giorni".:-))

Federico
Semplificando la formula, mi pare che y sia la resistenza risultante dall'aver messo in parallelo una resistenza da 100 ohm ed una da x ohm.

Shylock
Effettivamente sono un tipo molto apprensivo, ma questo calcolo non l'avevo mai fatto.
Allora diciamo meglio: per "nella vita di tutti i giorni" si può intendere "due grandezze che chi legge abitualmente il giornale si trova spesso davanti agli occhi"
(ma non si tratta di questioni...tipografiche!)

Enrico Delfini
Se 100 sono i lavoratori occupati e x la percentuale dei disoccupati, rispetto ai lavoratori, y=percentuale di disoccupati calcolata sull'universo dei lavoratori potenziali.
...però mi piaceva di più quella del meteorite.

Shylock
Sì le precedenti interpretazioni funzionano, ma non sono quelle a cui ho pensato io.
Aggiungo ancora due elementi: l'argomento è economico, una delle variabili è un dato "importante", ma forse la relazione riguarda un aspetto poco noto della variabile importante, perciò...avvertitemi quendo siete stufi!
...
Dal momento che siamo usciti dalla pagina provo a dare la mia interpretazione.
In realtà ritengo ci siano un'infinità di grandezze che possono essere legate in tale modo, perché la formula esprime quanto una grandezza diminuisca in percentuale rispetto a un'altra in funzione di quanto la seconda aumenti rispetto alla prima.
Nel mio caso avevo elaborato tale formula per mettere in relazione INFLAZIONE e AUMENTO DEI PREZZI, poiché (è cosa poco nota e ancor meno detta) l'inflazione non è la misura dell'aumento dei prezzi, ma della svalutazione della moneta. Non sono un economista, ma credo che su questo punto giornali e commentatori vari facciano sempre molta confusione. Ad esempio il dato mensile dell'ISTAT dovrebbe essere l'aumento dei prezzi, mentre il dato riassuntivo annuale fornito da Bankitalia credo sia l'inflazione.
Per tassi di svalutazione limitati le due grandezze sono abbastanza simili, ma quando sono alti (ricordiamoci che per quasi vent'anni abbiamo avuto un'inflazione a due cifre (1981: 21,8%!) la cosa diventa assai importante.
Un esempio dà subito l'idea: se i prezzi raddoppiano (+100%) vuol dire che il valore della moneta si dimezza (inflazione=50%).
Si può immaginare ad esempio che cosa succederebbe a quel signore che, dovendo vivere con la rendita di un capitale, volesse calcolare quanta parte della rendita dovrebbe accantonare per poter mantenere invariato il valore reale del capitale stesso, se scambiasse il tasso di inflazione con l'aumento dei prezzi.

Invertendo la formula (K= % aum. prezzi; i= % inflazione):

k=100i/(100-i)

Questo è tutto S.E.&.O.. Sono gradite integrazioni.

Enrico Delfini
Temevo ti fossi perduto tra le polveri leggere e i crittogrammi pesanti!
Nulla da eccepire sulla relazione inflazione/aumento dei prezzi: è la stessa del rischio di meteorite!!

Trovate il più piccolo intero n per cui sia 2n+1 che 3n+1 sono quadrati perfetti, e dimostrate che ogni altro numero con questa proprietà è multiplo di esso.

>>> Risposte & riflessioni
Francesco Veneziano
Prima che il quesito scompaia negli archivi, vorrei dare la soluzione.
2n+1=k^2
3n+1=j^2
Sommando membro a membro otteniamo
5n+2=k^2+j^2
k^2+j^=2mod5
un quadrato è congruente a 0/1/4 mod 5, di questi l'unica combinazione che sommata dà 2 è 1-1
Quindi sia k^2 che j^2 sono congruenti a 1 mod 5 e quindi n è multiplo di 5.

Un quadrato dispari è congruente a 1/9 mod 16, quindi o la seconda equazione diventa:
3n+1=16m+1
3n=16m
n è multiplo di 8

oppure diventa
3n+1=16m+9
3n=16m+8
n è multiplo di 8

In entrambi i casi n è multiplo di 8, ed essendo anche multiplo di 5, è multiplo di 40
QED

Enrico D.
Tutto chiaro, e quasi facile.
Per finire con i quadrati, voglio citare il celebre filosofo Walter Valdi che ha scritto:
"Mi sono sempre chiesto: ma chi va in giro a costruire quadrati sulle ipotenuse?"
P.S: W.V. non è un filosofo, ma un cabarettista milanese (a me peraltro ignoto) la cui citazione ho trovato in una rivista di cardiologia(!)

Sarebbe riservato ai ragazzi, ma metà dei miei amici "non fisico-matematici" ha dato una Risposte & riflessioni sbagliata.
Sulla Terra è l' equinozio di primavera, ma voi siete sulla Luna e vedete la Terra perpendicolarmente sopra di voi.
Dopo quanto tempo la vedrete tramontare?
Risposte & riflessioni possibili:
-dopo 6 ore
-dopo 12 ore
-dopo 14 giorni
-dopo 28 giorni
-nessuna delle precedenti

>>> Risposte & riflessioni
Archimede
Non la vedremo mai tramontare, infatti la Luna è sempre rivolta verso la Terra con la stessa "faccia". Questo è dovuto al fatto che la velocità di rotazione della Luna attorno alla Terra è equivalente alla velocità di rotazione su se stessa.

La combinazione di una cassaforte è composta da 10 cifre, inoltre:
la prima cifra indica il n° di "0" presenti nella combinazione
la seconda cifra indica il n° di "1" presenti nella combinazione
...
...
...
la decima cifra indica il n° di "9" presenti nella combinazione

Determinare la combinazione (potrebbe anche non essere unica)

Quello che propongo è un metodo per saggiare contemporaneamente la divisibilità per 7-11 - e 13.
Si divide il numero in triplette, a partire dalle unità (che è poi il modo normale di scrivere i numeri); si sommano il primo, terzo, quinto gruppo e si sottraggono i gruppi in posizione pari (secondo,quarto..). Il numero ottenuto, molto più corto e maneggevole, mantiene la divisibilità per 7 - 11 e 13 del numero iniziale.
Ciò è dovuto al fatto che 7*11*13=1001
Esempi: