[HOME - BASE Cinque - Appunti di Matematica ricreativa]

La scala appoggiata al muro

Un problema di meccanica con variazioni geometriche

La scala 1
Inviato da Pasquale il 15/03/05 17:21

Una scala a pioli appoggia a terra e contro un muro, con il quale forma un angolo alfa.
La scala ha massa m e il coefficiente di attrito c è uguale per il contatto sia col muro che col terreno.

Buon lavoro

Questo problema mi evoca la simbologia della scala.

Sali una scala.
Dove credi che ti porti?

Forse ti permetterà di vedere il mondo oltre il muro.

Le mie proposizioni illustrano così: colui che mi comprende, infine le riconosce insensate, se è salito per esse - su esse - oltre esse.
Egli deve gettar via la scala dopo che v'è salito.
Allora vede rettamente il mondo.
Ludwig Wittgenstein
Tractatus Logico Philosophicus

Spero che Rodney Smith non protesti per il copyright.

Forse ti permetterà di arrivare a te stesso.

Bronzo di Mak Hin Yeung.

La scala 2
Inviato da Paolo P. il 21/03/05 9:23:56

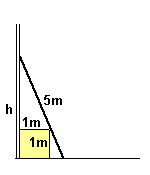
La solita scala appoggiata al solito muro.
La scala è lunga 5 m
Sotto la scala, appoggiata al suolo e a contatto con il muro, c’è una scatola cubica di lato 1 m
Qual’ è l’ altezza massima che può raggiungere la cima della scala, se la scala mantiene il contatto sia col muro che col terreno?

La scala 3
Inviato da Alcuino il 23/03/05 9:24:09

La solita scala (di lunghezza d) è inizialmente aderente alla parete verticale.

Con movimento continuo, e avendo cura di non distaccare mai la cima dalla parete, si fa scorrere il piede della scala sul pavimento fino a quando essa non risulti completamente distesa per terra.

L'insieme delle posizioni successivamente assunte dalla scala nel passaggio dalla posizione verticale a quella orizzontale costituisce l'inviluppo delle tangenti ad una curva. Quale?


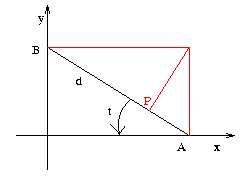
Il segmento BA rappresenta la scala in una posizione generica.
Il punto P è il generico contatto della curva di inviluppo con la scala.

La scala 4
Inviato da Paolo P il 23/03/05 9:48:05 [1]

Una gustosa variante, simmetrica di un problema che avevamo già discusso, che era: (dato lo stesso movimento della scala) che traiettoria descrive il punto medio della scala?

Ultimo aggiornamento: aprile 2005

Risposte & riflessioni

La scala 1
Alcuino, 19/03/05 17:17

Provo a risolvere il problema così:

Indichiamo con:
L la lunghezza della scala appoggiata alla parete nel punto A e al pavimento nel punto B;
Lg la distanza del baricentro dal piede della scala;
Lu la distanza dell’uomo dal piede della scala;
P1 il peso della scala applicato al baricentro;
P2 il peso dell’uomo sulla scala;
Ra e Rb le forze reattive vincolari (normali a parete e pavimento);
Aa e Ab le forze di attrito radente (parallele a parete e pavimento);
(x) è l’angolo tra scala e pavimento
f è il coefficiente di attrito radente tra scala e parete-pavimento.

Consideriamo che in un primo tempo alla scala siano complessivamente applicate la forza attiva P1, le forze reattive Ra e Rb e le forze di attrito Aa e Ab, ognuna secondo la propria direzione e verso.
Imponendo l’equilibrio secondo l’orizzontale si ha:

1) Ra = Ab.

Imponendo l’equilibrio secondo la verticale si ha:

2) Rb + Aa = P1

Imponendo l’equilibrio alla rotazione nel punto B si ha:

3) Ra*L*sin(x)+Aa*L*cos(x)=P1*Lg*cos(x).

Sostituendo e facendo un po’ di passaggi si arriva a:

4) tg(x) = (P1*Lg-Aa*L)/Ab*L

Poniamo Aa/Ra=m e Ab/Rb=n e sostituiamo nelle 1), 2) e 3). Si ricava

5) tg(x) = [Lg-(L-Lg)*m*n]/L*n

In condizioni di equilibrio dev’essere m <= f e n <= f, dove f è il coefficiente di attrito radente scala-parete e scala-pavimento. Di conseguenza la scala sarà in equilibrio se:

6) tg(x) >= [Lg-(L-Lg)*f^2]/L*f

Se sulla scala c’è un uomo vale quanto detto prima, a condizione di considerare il baricentro come baricentro del sistema scala + uomo.
La risultante sarà (P1+P2) e la distanza del nuovo baricentro dal piede della scala

7) Lg = [P1*L/2 + P2*Lu]/(P1+P2)

determinata con un’equazione di momento nel punto B.

Sostituendo la 7) nella 6) infine si ottiene

8) tg(x) >= [P1*L-L(P1+2*P2)f^2+2*P2*Lu(1+f^2)]/[2*L(P1+P2)f]

Da questa formula si vede che, al crescere di Lu, cioè man mano che l’uomo si trova più in alto sulla scala, per evitare cadute, tg(x) dev'essere maggiore, cioè la scala dev’essere più ripida. Infine quando l’uomo sta in cima (quindi Lu=L) la 8) diventa

9) tg(x) >= [2*P2 + P1(1-f^2)]/[2(P1+P2)f]

che è la condizione perché l’equilibrio avvenga in qualsiasi posizione si trovi l’uomo sulla scala.

Consideriamo che il coefficiente di attrito radente è < 1 e varia tra 0,15 e 0,20 per i metalli più comuni e arriva a 0,75 per pietre rugose.
Facciamo qualche calcolo con f = 0,5 e un uomo di 80 kg che sale su una scala di 20 kg si ha un angolo tra scala e pavimento di circa 60°.

La scala 2
Montnoir, 21/03/05 18:29:06
Hmax = 4,84 (valore approssimato)
Qui l'equazione trigonometrica risolvente è
5*sin(x)- tg(x) - 1 = 0
da cui si ricava un angolo tra pavimento e scala di 1.316 rad.

Lucky, 21/03/05 20:09:33
Beh, c'è anche un modo geometrico per risolvere il problema:
si scrive l'equazione della retta passante per i punti A=(a,0) e B=(0,b) e si ottiene (forma parametrica):
x/a + y/b = 1
Poi si impone il passaggio per il punto P=(1,1). Si ottiene la condizione
1) 1/a + 1/b =1
che, associata all'altra,
a^2 + b^2 = 25
con pochi passaggi conduce all'equazione
(ab)^2 - 2ab - 25 = 0
la cui unica soluzione positiva è:
2) ab = [2+sqrt(104)]/2 = 6,099...
D'altra parte, dalla condizione 1) si ricava che è anche
(a+b) = 6.099...
da cui b = [2+sqrt(104)]/2 - a
che, sostituito nella 2), conduce all'equazione
a^2 - a[2+sqrt(104)]/2 + [2+sqrt(104)]/2 = 0
le cui due soluzioni positive
a1 = 4,838501161...
a2 = 1,260518353...
risolvono completamente il problema, rappresentando rispettivamente le distanze della cima e del piede della scala dal punto di intersezione della parete e del pavimento.

Lucky, 21/03/05 20:17:12
Dico meglio, rappresentano le distanze del piede della scala dalla parete nelle due posizioni possibili:
1) con la scala quasi orizzontale
2) con la scala quasi verticale.
E' chiaro che, per simmetria, la distanza della cima della scala dal pavimento ha gli stessi valori, ma invertiti.

Gianfranco Bo, 21/03/05 22:07:28
Complimenti, risposte esatte e soluzioni valide.
Buona quella di Lucky che rimane nell'ambito delle eq. di 2° grado.
Posto anche la mia soluzione, visto che ho faticato un po' a scriverla.
Indico con:
1+y la quota del punto in cui la scala tocca il muro;
1+x la distanza dalla base del muro del punto in cui la scala tocca il pavimento.
Applico il teorema di Pitagora:
(x+1)^2 + (y+1)^2 = 25
Ho un'equazione e due incognite, ma...
osservando dei triangoli simili, posso dire che:
1:y = x:1
ovvero, ecco la seconda equazione:
xy=1; y=1/x
ed ecco la risolvente (di 4° grado)
x^2 + 1/x^2 + 2x + 2/x - 23 = 0
x^4 + 2x^3 - 23x^2 + 2x + 1 = 0
x=0.2605183...
y=3.8385...
Per cui l'altezza massima è:
4.8385 m (circa)

La scala 3
Un piccolo suggerimento di Alcuino.
L’enunciato chiariva che “l'insieme delle posizioni successivamente assunte dalla scala nel passaggio dalla posizione verticale a quella orizzontale costituisce l'inviluppo delle tangenti ad una curva. Da ciò si deduce che la scala è in ogni posizione tangente alla curva e, pertanto, deve avere in ogni posizione un punto in comune con essa. Quindi anche nel punto x=0, dove per l’appunto è f(0)=L. Se, come sostieni tu, fosse f(0)=+infinito quale sarebbe il punto della scala tangente alla curva? Potrei aggiungere che simmetricamente è pure f(L)=0.
D’altra parte, se si prova a disegnare qualcuna delle posizioni assunte dalla scala, partendo dalla verticale e giungendo all’orizzontale, l’insieme dei segmenti dà subito l’idea della curva che stiamo cercando. Inoltre, si vede bene che, man mano che la scala tende all’orizzontale, il punto di tangenza si sposta lungo di essa e, più precisamente, nel punto x=0 coincide con la cima e nel punto x=L coincide con il piede.
Quindi qui siamo in presenza di una curva che, partendo dal punto f(0)=L, dopo aver descritto una certa traiettoria, finisce nel punto f(L)=0.
Si tratta di scriverne l’equazione.

Cesarone
Bisogna trovare la retta che contiene il segmento in questione e questo passo è facile.
Ovviamente la retta sarà in funzione di un parametro, ovvero una famiglia di curve F(x,y,c)=0, dove c è il parametro.
Si deriva la F rispetto a c e la si pone uguale a 0. Così facendo si ricava c in funzione di x. Si sostituisce dentro ad F e si ottiene la F(x,y)=0.

Per completezza vi riporto il risultato. In ogni modo sfrutto la teoria dell’inviluppo sopra esposta.

Cerco la famiglia di rette che contiene il segmento di lunghezza L cercato.

In generale: y = mx + q.

Deve valere in questo caso:

q^2 + (-q/m)^2 = L^2

Da qui ricavo l’equazione parametrica delle rette :

y + q*x / sqrt(L^2 – q^2) –q = 0

Questa equazione è appunto la F(x,y,q)=0.
Derivo la F rispetto al parametro q e pongo uguale a zero, ottenendo:

q = sqrt[L^2 – (x*L^2)^(2/3) ]

Inserendo questo parametro nella F(x,y,q)=0 ottengo l’equazione della curva inviluppo cercata.
A voi scoprire se si tratta di una curva nota…

Gianfranco Bo
Complimenti a Cesarone per la risposta esauriente.
Aggiungo soltanto qualche informazione.
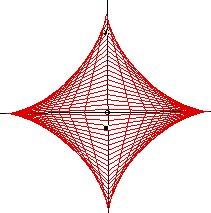
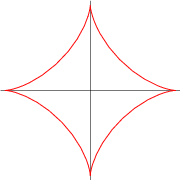
L'inviluppo richiesto da Alcuino è una curva che si chiama Asteroide ed ha la seguente equazione parametrica:

x = d cos3(t)
y = d sin3(t)

dove d è la lunghezza della scala.

Passando in coordinate cartesiane, l'equazione è:
x2/3 + y2/3 = d2/3

Naturalmente la scala "scivola" soltanto nel 1° quadrante.
Per ottenere l'Asteroide completo dobbiamo immaginare che la scala compia lo stesso movimento in tutti i quadranti.


Asteroide

L'Asteroide è un'ipocicloide a 4 cuspidi

La scala 4
Alcuino
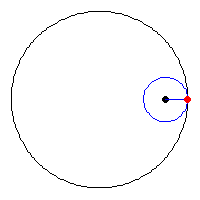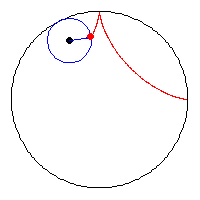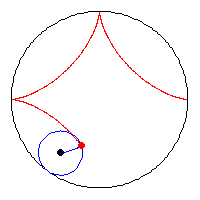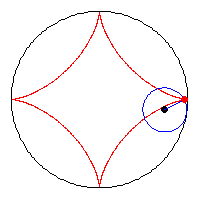
La traiettoria descritta dal punto medio della scala è un quarto di circonferenza, col centro nell’intersezione parete-pavimento e raggio uguale a L/2. Solo che scrivere quest’equazione è stato un po’ più semplice.
E’ pure evidente la diversità dei due problemi se si considera che nell’esempio da te citato il punto della scala, appartenente anche alla curva, è sempre uno (quello medio), mentre nel mio caso esso è variabile lungo di essa.

Sito Web realizzato da Gianfranco Bo