[BASE Cinque - Appunti di Matematica ricreativa]
Ci sono esattamente n modi diversi di disegnare questo fiore.
OK, ma come si fa a contarli?
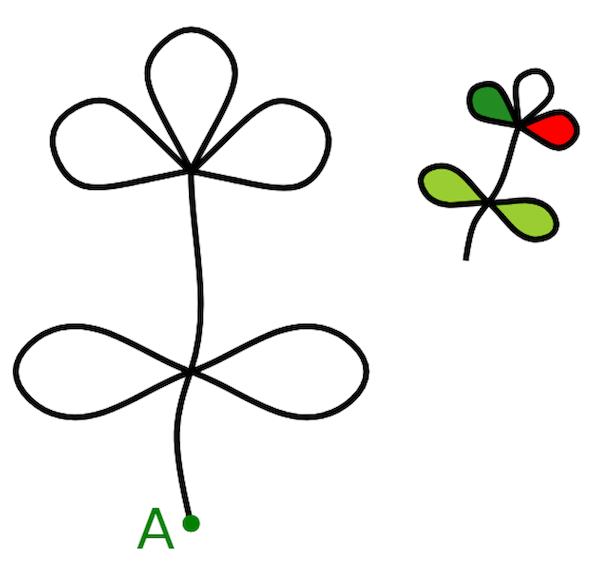
Provate a disegnare questo fiore, partendo dal punto A, con un solo tratto di
penna, senza mai sollevarla dal foglio e senza ripassare su una linea già
tracciata.
Ci sono esattamente 384 modi diversi per farlo.
Dipende
dall'ordine in cui tracciate le foglie e i petali e se scegliete il senso orario
o quello antiorario.
Domande.

Immaginate il disegno del fiore come un grafo.
---
Grafo. Un grafo è una rappresentazione matematica formata da vertici (punti) e archi (linee) che collegano i vertici.
---
Nel nostro fiore, i vertici sono i punti di snodo delle foglie e dei petali, mentre gli archi sono i tratti che uniscono questi punti.
Disegnare il fiore con un solo tratto di penna, senza sollevarla e senza ripassare significa percorrere il grafo seguendo gli archi una sola volta.
Il percorso parte da A ma non ritorna ad A, perciò è un cammino euleriano.
---
Cammino euleriano. Un cammino euleriano è un percorso in un grafo che attraversa tutti gli archi passando su ciascun arco esattamente una volta.
---
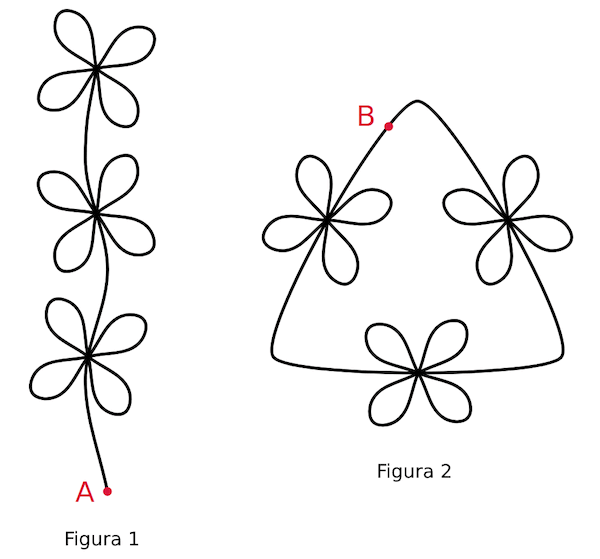
Provate a disegnare la figura 1, partendo dal punto A, con un solo tratto di
penna, senza mai sollevarla dal foglio e senza ripassare su una linea già
tracciata.
Stesso esercizio per la figura 2, partendo dal punto B e
ritornando a B.
Domanda.
1. In quanti modi diversi si può tracciare
ciascuno dei due disegni?
---
Pensierino.
Una risposta possibile per la figura 2
potrebbe essere:
(2)⋅((4⋅2)⋅(3⋅2)⋅(2⋅2)⋅(1⋅2))3
= 113.246.208
Se ne disegniamo 2 al minuto, ci mettiamo circa un secolo.
Ma avremo solo
sprecato carta, inchiostro e tempo perché i disegni sono tutti uguali!
Provate a disegnare questo fiore, partendo dal punto A, con un solo tratto di
penna, senza mai sollevarla dal foglio e senza ripassare su una linea già
tracciata.
Ci sono esattamente 384 modi diversi per farlo.
Domande.
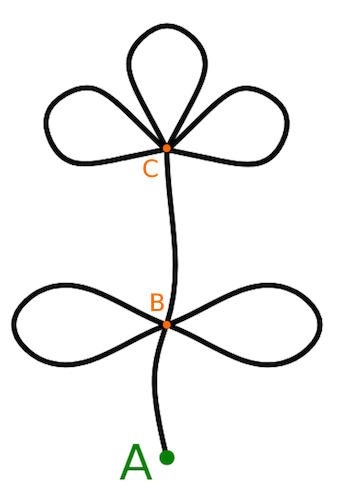
Questa è la mia soluzione elementare, diciamo naif, ingenua.
---
Enumerare le
possibilità.
Parti da A e arriva all'incrocio B delle foglie.
1
Disegna una delle 2 foglie in uno dei 2 versi (orario-antiorario):
2×2
Disegna la foglia rimanente, in uno dei due versi:
1×2
Prosegui
arrivando alla base C del fiore.
1
Disegna uno dei 3 petali in uno dei 2 versi:
3×2
Disegna uno dei 2
petali rimanenti in uno dei 2 versi:
2×2
Disegna l'ultimo petalo in in uno
dei 2 versi:
1×2
Totale delle possibilità: 1×((2×2)×(1×2))×1×((3×2)×(2×2)×(1×2)) = 384
---
Questa è una soluzione combinatoria più matura.
Non consideriamo i petali e le foglie ma le strade che escono da ciascun nodo.
Ci mettiamo cioè in un atteggiamento locale piuttosto che globale. Immaginiamo di essere una formica che arriva in un nodo, vede solo le uscite disponibili e decide cosa fare.
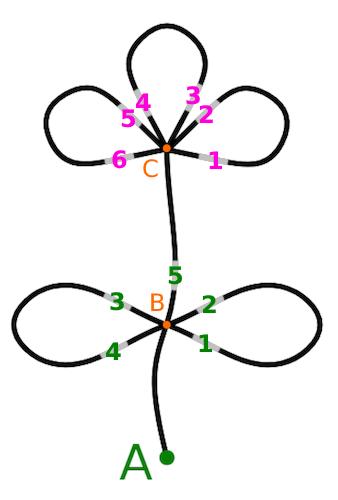
Partiamo da A e arriviamo al primo incrocio, B.
Ci sono 5 uscite possibili ma
non possiamo proseguire dritti finché non abbiamo percorso le due foglie, quindi
abbiamo solo 4 strade da scegliere.
4
Conclusa la prima foglia (loop), ci ritroviamo al punto B e possiamo scegliere fra altre 2 strade.
2
Proseguiamo fino al secondo incrocio C. Qui abbiamo 6 strade tra cui scegliere.
6
Percorso il primo petalo (loop) ci rimane una scelta tra 4 strade
4
Percorso il secondo loop ci rimane una scelta tra 2 strade.
2
Totale: (4⋅2)⋅(6⋅4⋅2) = 4!!⋅6!! = 384
---
Semifattoriale.
Le scritture del tipo n!! (con n numero naturale), indicano il semifattoriale di un numero.
---
Il semifattoriale di un numero intero positivo n è il prodotto di tutti i numeri interi positivi minori o uguali di n che hanno la stessa parità di n.
Si scrive così: n!!
Esempi.
---
Provate a disegnare la figura 1, partendo dal punto A, con un solo tratto di
penna, senza mai sollevarla dal foglio e senza ripassare su una linea già
tracciata.
Stesso esercizio per la figura 2, partendo dal punto B e
ritornando a B.
Domanda.
1. In quanti modi diversi si può tracciare
ciascuno dei due disegni?

Per risolvere (velocemente) i problemi, ricaviamo una formula generale dal procedimento 3 dell'esercizio precedente.
---
Se abbiamo uno stelo con f fiori di p petali ciascuno, possiamo tracciarlo in n modi possibili, con:
n = ((2p)!!)f
---
Figura 1.
f = 3; p = 4;
n = (8!!)3 = 3843 = 56.623.104
Figura 2.
Nella figura 2 si parte da B e si ritorna al punto di partenza. Questo si chiama circuito euleriano.
Il numero di modi di disegnarlo è il doppio della figura 1 perché quando partiamo B abbiamo 2 scelte di direzione.
n = 2⋅(8!!)3 = 3843 = 113.246.208
---
Ringraziamento. Ringrazio il professore Riccardo Moschetti per avermi suggerito la soluzione col fattoriale doppio, in una bella narrazione!!
---
#Grafo #CamminoEuleriano #CicloEuleriano #UnaLinea
---
Pace e bene a tutti.
GfBo
Data creazione: dicembre 2025
Ultimo aggiornamento: dicembre 2025
html5
Sito Web realizzato da Gianfranco Bo