[BASE Cinque - Appunti di Matematica ricreativa]
Affrontare un problema matematico diventa un'esperienza potente quando ti consente di esplorare la tua rete di conoscenze personali. Di diventarne consapevole. Di espanderla. Credo che per un Matematico sia una sorta di esercizio spirituale.
---
Problema 1. Numeri sui vertici di un cubo
Assegna un numero da 0 a 7, senza ripetizioni, a ciascun vertice di un cubo in modo tale che la somma degli estremi di ogni spigolo sia un numero primo.

---
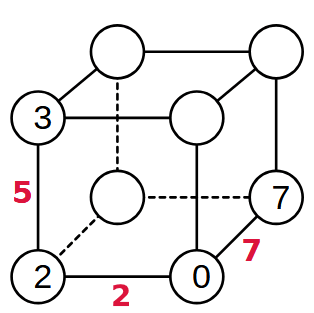
Ecco, per esempio un tentativo di soluzione parziale che rispetta le condizioni. Ma NON è la soluzione corretta.
Non metterti subito all'opera per risolvere il problema ma prima esplora le aree della tua rete personale di conoscenze che si accendono alla lettura del problema. Anche quelle più elementari!
Ciascuno di noi ha una rete di conoscenze diversa, quindi ti propongo qualche spunto che potrebbe essere diverso dai tuoi.
E così via.
Vediamo alcuni aspetti indispensabili per risolvere il problema.
Se vuoi cercare la soluzione lavorando su una figura, conviene usare una rappresentazione planare del cubo. E' più facile da verificare.
Grafo tridimensionale del cubo |
Grafo planare del cubo |
E' importante osservare che ogni vertice è collegato con altri tre vertici.
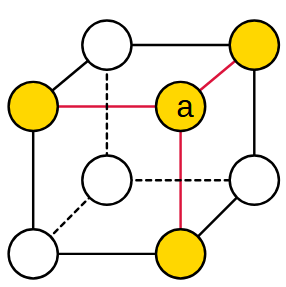
Il vertice a è collegato con altri tre vertici |
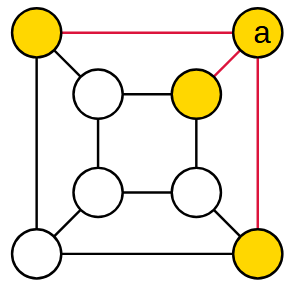
Il vertice a è collegato con altri tre vertici |
Visto che ogni vertice è collegato ad altri tre, bisogna controllare una condizione necessaria affinché il problema sia risolvibile.
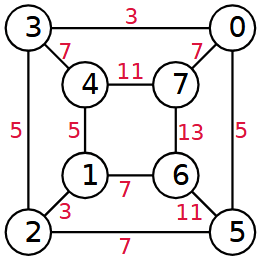
Scrivi tutte le coppie che hanno come somma un numero primo e verifica che ogni numero da 0 a 7 compaia in almeno tre coppie.
|
Somma |
Coppie |
|
2 |
(0,2) |
|
3 |
(0,3), (1,2) |
|
5 |
(0,5), (1,4), (2,3) |
|
7 |
(0,7), (1,6), (2,5), (3,4) |
|
11 |
(4,7), (5,6) |
|
13 |
(6,7) |
Altre domande sul problema 1
Ecco tre possibili domande, ma tu potresti averne molte altre.
Problema 2. Facce costanti
Etichetta i vertici di un cubo con i numeri 1, 2, 3, 4, 5, 6, 7, 8 senza ripetizioni, in modo che la somma dei numeri ai quattro vertici di ciascuna faccia sia costante.

Altre domande sul problema 2.
a) Quale deve essere l'unica somma possibile dei numeri su ciascuna faccia del cubo?
b) Quante soluzioni distinte ha il problema, a meno di rotazioni del cubo?
---
Nota.
L'ispirazione per questo articolo è nata da due problemi che ho trovato nel libro di Paul Yiu, Recreational Mathematics, Department of Mathematics, Florida Atlantic University, 2003.
Problema 1. Numeri sui vertici di un cubo
Assegna un numero da 0 a 7, senza ripetizioni, a ciascun vertice di un cubo in modo tale che la somma degli estremi di ogni spigolo sia un numero primo.
 |
 |
Altre domande sul problema 1.
Per le prime due domande i lavori sono ancora in corso...
Per la terza domanda, segnalo una cosa carina, che mi ha sorpreso.
Il sistema di A.I. Perplexity in versione freemium, come tanti altri, è basato sul testo e non sulle immagini. Perciò deve trovare un modo "testuale" di rappresentare e "vedere" il cubo come grafo.
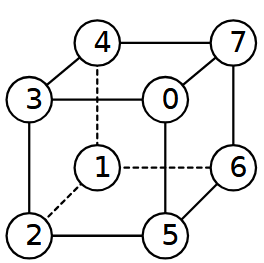
Ebbene, ha associato ciascuno degli 8 vertici del cubo a numero binario di 3 bit, come illustrato qui sotto. I tre bit sono le coordinate 3D dei vertici di un cubo di spigolo lungo 1.
| A (000) B (001) C (010) D (011) E (100) F (101) G (110) H (111) |
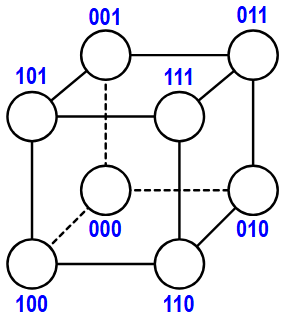 Gli 8 vertici del cubo associati a numeri binari |
Come identifica le coppie di vertici connessi da uno spigolo?
Usa questa proprietà: Due vertici del cubo sono connessi da uno spigolo se e solo se i loro numeri binari differiscono esattamente in una sola cifra.
In altre parole, due vertici sono connessi quando la distanza di Hammig dei loro codici binari è 1.
Forte, vero?
In realtà sapevo queste cose e conoscevo la distanza di Hamming, ma non mi erano venute in mente affrontando il problema. L'Intelligenza Artificiale me le fatte ricordare e ha consolidato la mia rete di conoscenze. Buono, direi.
---
Problema 2. Facce costanti
Etichetta i vertici di un cubo con i numeri 1, 2, 3, 4, 5, 6, 7, 8 senza ripetizioni, in modo che la somma dei numeri ai quattro vertici di ciascuna faccia sia costante.
Ecco, per esempio, una delle 6 soluzioni possibili.
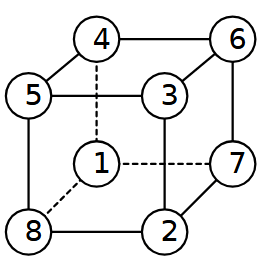 |
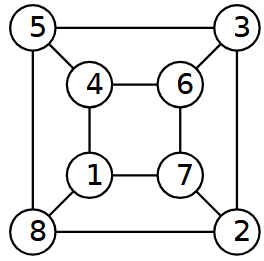 |
Altre domande sul problema 2.
a) Quale deve essere l'unica somma possibile dei numeri su ciascuna
faccia del cubo?
Risposta: 18
b) Quante soluzioni distinte ha il problema, a meno
di rotazioni del cubo?
Risposta: 6
---
Pace e bene a tutti.
GfBo
Data creazione: luglio 2025
Ultimo aggiornamento: luglio 2025
html5
Sito Web realizzato da Gianfranco Bo