[BASE Cinque - Appunti di Matematica ricreativa]
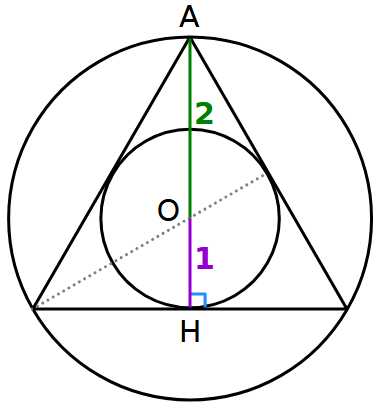
Una proprietà semplice ma sorprendente del triangolo equilatero è che il raggio della circonferenza circoscritta è il doppio del raggio della circonferenza inscritta.
Domanda 1.
Provate a dimostrarlo mentalmente, basandovi sulla figura qui sotto.

---
Domanda 2.
Prendete come unità il raggio della circonferenza inscritta e calcolate le seguenti misure.
Triangolo equilatero
circoscritto a una circonferenza di raggio 2
| apotema | 1 |
| raggio | 2 |
| altezza | ...... |
| lato | ...... |
| area cerchio inscritto | ...... |
| area cerchio circoscritto | ...... |
| area del triangolo | ...... |
---
Ora coloriamo alcune parti della figura come mostrato qui sotto.
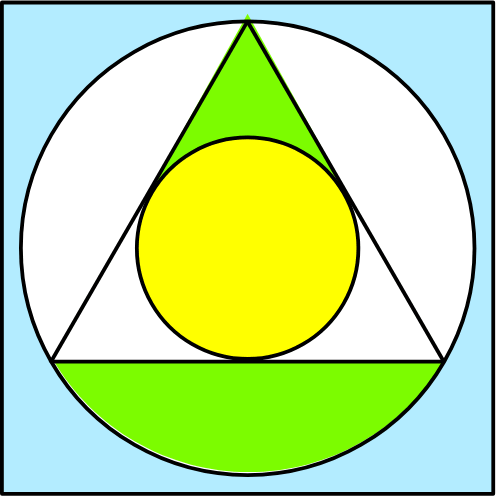
Domanda 3.
Dimostrate che la parte colorata di verde è equivalente alla parte colorata di giallo (cioè ha la stessa area).
giallo = verde
Se non volete rispondere alla domanda 3, non c'é problema.
Siete
autorizzati a prendere l'uguaglianza come assioma e usarla per la
prossima domanda.
---
Domanda 4.
Usate l'uguaglianza dimostrata nella domanda 3 per dimostrare che le aree gialla e verde messe assieme sono uguali all'area bianca.
giallo + verde = bianco
---
Ho preso lo spunto per questo articolo dal libro di Brian J. McCartin, Mysteries of the equilateral triangle, 2010.
Lo potete trovare facilmente in rete.
Brian J. McCartin, professore di Matematica Applicata presso la Kettering University (Michigan, USA), apre il volume con una dedica che mi ha fatto sorridere:
Dedicated to our beloved
Beta Katzenteufel
for completing our equilateral triangle.
E' la prima volta che vedo un libro dedicato a... un gatto!
Infatti, la fotografia che compare sotto la dedica chiarisce il tono affettuoso della frase: Beta gatto-diavolo è l’animale domestico che completa il triangolo equilatero della famiglia dell’autore.
Domanda 1.
Una proprietà semplice ma sorprendente del triangolo equilatero è che il raggio della circonferenza circoscritta è il doppio del raggio della circonferenza inscritta.
Provate a dimostrarlo mentalmente, basandovi sulla figura qui sotto.

Domanda 2.
Prendete come unità il raggio della circonferenza inscritta e calcolate le seguenti misure.
Triangolo equilatero
circoscritto a una circonferenza di raggio 2
| apotema | 1 |
| raggio | 2 |
| altezza | 3 |
| lato | 2√3 |
| area cerchio inscritto | π |
| area cerchio circoscritto | 4π |
| area del triangolo | 3√3 |
---
In generale: l'area del cerchio circoscritto a un triangolo equilatero è il quadruplo dell'area del cerchio inscritto.
---
Domanda 3.
Dimostrate che la parte colorata di verde è equivalente alla parte colorata di giallo (cioè ha la stessa area).
giallo = verde
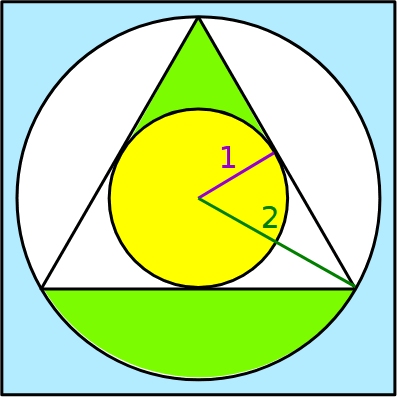
Usiamo il fatto che l'area del cerchio grande è il quadruplo dell'area de cerchio piccolo, giallo.
---
Domanda 4.
Usate l'uguaglianza dimostrata nella domanda 3 per dimostrare che le aree gialla e verde messe assieme sono uguali all'area bianca.
giallo + verde = bianco
Dimostrazione con riscrittura.
Ecco per esempio una dimostrazione basata quasi esclusivamente su un sistema di riscrittura formale.
Dimostrazione.
C.V.D.
Una giustificazione.
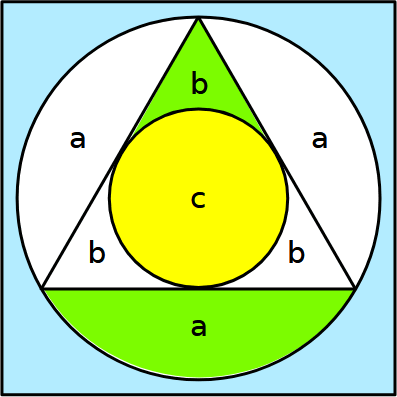
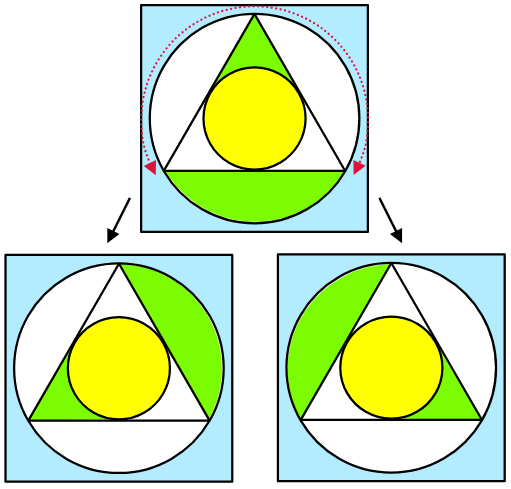
Se vogliamo giustificare l'inserimento delle lettere a, b, c, nella figura precedente, possiamo usare la simmetria rotazionale.
Infatti, una rotazione di 120° intorno al centro porta la punta verde e il segmento circolare verde nelle parti bianche corrispondenti.
Con 2 rotazioni di +120° e -120°, la parte verde copre tutto il bianco, come mostrato nelle figure seguenti. E come bonus possiamo dedurre che il verde è metà del bianco.
Grazie a Francesco C. per questa osservazione.
---
Pace e bene a tutti!
GfBo
Data creazione: gennaio 2026
Ultimo aggiornamento: gennaio 2026
html5
Sito Web realizzato da Gianfranco Bo