[HOME - BASE Cinque - Appunti di Matematica ricreativa]

Proposizione su un capofamiglia

52. Propositio de homine paterfamilias

LII. PROPOSITIO DE HOMINE PATERFAMILIAS.
Quidam paterfamilias jussit XC modia frumenti de una domo sua ad alteram deportari; quae distabat leucas XXX: ea vero ratione, ut uno camelo totum illud frumentum deportaretur in tribus subvectionibus, et in unaquaque subvectione XXX modia portarentur: camelus quoque in unaquaque leuca comedat modium unum. Dicat, qui velit, quot modii residui fuissent?
Solutio.
In prima subvectione portavit camelus modios XXX super leucas X, et comedit in unaquaque leuca modium unum, id est, modios XX comedit et remanserunt X. In secunda subvectione similiter deportavit modios XXX et ex his comedit XX, et remanserunt X, in tertia vero subvectione fecit similiter; deportavit modios XXX, et ex his comedit XX, et remanserut X. Sunt vero de his, qui remanserunt, modia XXX, et de itinere leucae X. Quos XXX, in quarta subvectione domum detulit, et ex his X in itinere comedit, et remanserunt de tota illa summa modia tantum XX.

LII. PROPOSIZIONE SU UN CAPOFAMIGLIA.
Un capofamiglia ordinò che 90 moggi di frumento fossero portati da una delle sue case ad un'altra, distante 30 leghe. Dato che il carico di frumento poteva essere portato da un cammello in 3 viaggi, e dato che il cammello mangia un moggio per lega, dica, chi vuole, quanti moggi rimasero [alla fine del trasporto]?
Soluzione.
Nel primo viaggio il cammello portò 30 moggi per 10 leghe, mangiando un moggio di grano per lega; cioè, mangiò 20 moggi e ne lasciò 10.
Nel secondo viaggio, portò ugualmente 30 moggi, mangiandone 20 e lasciandone 10.
Nel terzo viaggio fece la stessa cosa, portando 30 moggi, mangiandone 20 e lasciandone 10.
Quindi rimasero 30 moggi e 10 leghe da percorrere.
Il cammello portò questi 30 moggi in un quarto viaggio durante il quale ne mangiò 10 lasciandone soltanto 20 di tutto il carico originario.

Nota.
Questo, per me, è il quesito più interessante e sconcertante di tutta la raccolta.
Si tratta di un problema difficile: ha molte soluzioni, non è facile trovarle tutte e individuare quella ottima, con tanto di dimostrazione.
Questo problema compare per la prima volta nelle "Propositiones" di Alcuino e quindi sembrerebbe esserne egli l'autore.
D'altra parte la soluzione data da Alcuino è evidentemente errata e comunque non spiega la strategia utilizzata per trovarla. Quale sarà stata la fonte di questo problema?
Quali sono gli errori più evidenti nella soluzione di Alcuino?
1) nel testo si parla di 3 viaggi mentre nella soluzione se ne indicano 4
2) non è chiaro il tragitto percorso dal cammello nel terzo viaggio
3) Alcuino non sembra tener conto del fatto che nel terzo viaggio il cammello non deve tornare indietro.
4) dopo il terzo viaggio non rimangono 10 leghe da percorrere, bensì 20

La soluzione ottimale nel caso di 2 tratte.
Una cosa certa è che la soluzione di Alcuino prevede di dividere il percorso in due parti o tratte.
Il cammello deposita una certa quantità di grano in un punto opportuno e la raccoglie nell'ultimo viaggio.

Esempio 1: una strategia poco efficiente.
Supponiamo di fissare un punto a metà percorso, cioè a 15 leghe dalla partenza.

|-------------|--------------|
A...........B............C
0...........15...........30

1) nel primo viaggio il cammello percorre AB e ritorno consumando 30 moggi di grano
2) nel secondo viaggio il cammello percorre AB e ritorno consumando 30 moggi di grano
3) nel terzo viaggio il cammello percorre AC consumando 30 moggi di grano
Con questa strategia si giunge a destinazione senza neanche un moggio di grano.

Esempio 2: una strategia più efficiente
Se vogliamo migliorare la strategia dobbiamo accorciare la prima tratta. Spostiamo il punto B indietro di 1 lega.

|------------|---------------|
A..........B.............C
0..........14............30

1) nel primo viaggio il cammello percorre AB e ritorno consumando 28 moggi di grano e depositandone 2 nel punto B
2) nel secondo viaggio il cammello percorre AB e ritorno consumando 28 moggi di grano e depositandone 2 nel punto B
3) nel terzo viaggio il cammello percorre AB consumando 14 moggi di grano, raccoglie quindi i 4 moggi depositati in precedenza e completa il viaggio consumando altri 16 moggi e depositando in C 4 moggi di grano
Con questa strategia si riesce a trasportare destinazione 4 moggi di grano.

Chiediamoci: qual è il punto migliore in cui fissare la prima tappa?
E' quel punto da cui il cammello può partire con 30 moggi, che è il suo massimo carico, per concludere l'ultimo viaggio.

Dove si trova quel punto?
Per trovarlo chiamiamo:
30 = AC, la distanza totale da percorrere
15 - t = AB, la lunghezza della prima tratta

Sostituendo, si ha che:
1) nel primo viaggio il cammello percorre AB e ritorno consumando 2(15-t) moggi di grano e depositandone 2t nel punto B
2) nel secondo viaggio il cammello percorre AB e ritorno consumando 2(15-t) moggi di grano e depositandone 2t nel punto B
3) nel terzo viaggio il cammello percorre AB consumando (15-t) moggi di grano, raccoglie quindi i 4t moggi depositati in precedenza e completa il viaggio consumando altri 15+t moggi e depositando in C (30-15-t) = 15-t moggi di grano

Facendo riferimento al terzo viaggio, noi vogliamo che:
30-(15-t)+4t = 30
cioè che:
-(15-t)+4t = 0
5t = 15
t = 3

Dunque:
AC = 30
AB = 15-3 = 12
moggi trasportati a destinazione = 15-3 = 12

|----------|-----------------|
A........B...............C
0........12..............30

Vediamo se funziona:
1) nel primo viaggio il cammello percorre AB e ritorno consumando 24 moggi di grano e depositandone 6 nel punto B
2) nel secondo viaggio il cammello percorre AB e ritorno consumando 24 moggi di grano e depositandone 6 nel punto B
3) nel terzo viaggio il cammello percorre AB consumando 12 moggi di grano, raccoglie quindi i 12 moggi depositati in precedenza e completa il viaggio consumando altri 18 moggi e depositando in C 12 moggi di grano
Con questa strategia si riesce a trasportare destinazione 12 moggi di grano.

La soluzione può essere rappresentata con il disegno seguente:

Si può trovare una soluzione migliore dividendo il percorso in 3 tratte
Il nocciolo del problema è riuscire a depositare 30 moggi di grano (il massimo carico trasportabile) il più vicino possibile alla destinazione.
Ecco una possibile soluzione.
Dividiamo il tragitto in tre tappe poste a 6, 16 e 30 leghe dal punto di partenza. Le tappe corrispondono a 1/5, 1/5+1/3 e 3/3 del tragitto da percorrere.

90..60.....30...........14 moggi
|----|---------|-------------|
A...B.......C...........D
0....6.......16..........30 leghe

Prima tappa
In 3 viaggi, dalla partenza alla lega 6, riusciamo a depositare 18+18+24 = 60 moggi alla lega 6.
Spiegazione: in ciascuno dei primi due viaggi il cammello parte con un carico di 30 moggi ma deve compiere andata e ritorno perciò mangia 12 moggi di grano e vengono depositati 18 moggi.
Nel terzo viaggio il cammello parte con un carico di 30 moggi e, non dovendo più tornare indietro, mangia 6 moggi e vengono depositati 24 moggi.

Seconda tappa
In altri 2 viaggi, dalla lega 6 alla lega 16, riusciamo a depositare 10+20 = 30 moggi alla lega 16.
La spiegazione è analoga a quella della prima tappa.

Terza tappa
In un viaggio il cammello percorre le ultime 14 leghe e porta a destinazione 30-14 = 16 moggi di grano.

La soluzione può essere rappresentata con il disegno seguente.

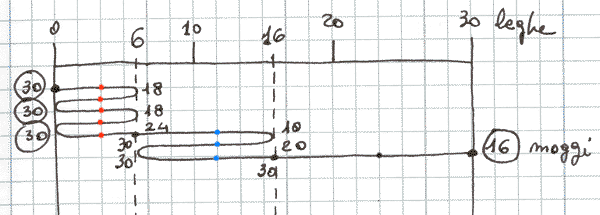
Ma in che modo è stata trovata questa soluzione?

Osserviamo innanzitutto che il percorso è diviso in tre parti, di cui:
- la prima, lunga 6 leghe, viene percorsa 5 volte (bollini rossi);
- la seconda, lunga 10 leghe, viene percorsa 3 volte (bollini blu);
- la terza, lunga 14 leghe, viene percorsa 1 volta (bollino nero).

Per rendere più efficiente il trasporto l'obiettivo è quello di depositare al termine di ogni tratta un MULTIPLO ESATTO del massimo carico trasportabile, cioè (30, 60, 90 moggi)
Questo criterio ci fornisce un metodo per calcolare la lunghezza delle prime due tratte. La terza viene di conseguenza.
Ecco come si fa.

Osserviamo innanzi tutto che i moggi inizialmente sono 90 = 3*30 e quindi occorreranno 3 viaggi.

Troviamo ora il punto in cui possiamo depositare 60 moggi in 3 viaggi.
Sia x la lunghezza della prima tratta. Facendo riferimento alla figura, avremo che:
90 - 5x = 60
5x = 30
x = 6

Troviamo infine la lunghezza della seconda tratta, al termine della quale possiamo depositare 30 moggi in 2 viaggi.
Sia y la lunghezza della seconda tratta. Facendo riferimento alla figura, avremo che:
60 - 3y = 30
3x = 30
x = 10

Questo problema è interessante perché lascia aperti molti interrogativi, ad esempio:
1) alle condizioni date, è possibile portare a destinazione più di 16 moggi di grano?
2) come si potrebbe generalizzare il problema?
3) come si potrebbero risolvere problemi di questo tipo con l'aiuto del computer?

Un esempio più generale
Consideriamo una variante al problema di Alcuino.
Un capofamiglia ordina che 420 moggi di frumento siano portati da una delle sue case ad un'altra, distante 105 leghe. Il carico di frumento deve essere portato da un cammello che può trasportare non più di 105 moggi alla volta.
Dato che il cammello mangia un moggio di frumento per lega, dica, chi vuole, quanti moggi possono essere trasportati a destinazione?

Osserviamo subito che 420 = 4*105
Estendendo i casi precedenti stabiliamo di dividere il tragitto in 4 tratte (420 moggi/105 moggi) e disegnamo lo schema seguente, dove a, b, c, d sono le lunghezze delle tratte, ancora incognite.
Possiamo tuttavia disegnare lo schema perché il nostro obiettivo è di fare successivamente 4, 3, 2, 1 viaggi, partendo ogni volta col carico massimo di 105 moggi di grano.

Procedendo analogamente al caso di 3 tappe calcoliamo:
4*105 - 7a = 3*105
a = 105/7

3*105 - 5b = 2*105
b = 105/5

2*105 - 3c = 105
c = 105/3

In questo modo arrivano a destinazione a + b + c moggi

Una possibile generalizzazione.
Continua...

Perché questo problema è stato classificato da David Singmaster "Jeep problem" o "Explorer problem"?
Continua...

Sito Web realizzato da Gianfranco Bo