
[BASE Cinque - Appunti di Matematica ricreativa]
Cosa scrisse veramente Giuseppe
Peano
a proposito della sua famosa curva frattale?
Nel 1890 Giuseppe Peano (1858–1932) pubblicò un articolo intitolato “Sur une courbe qui remplit toute une aire plane” sui Mathematische Annalen.
In quell'articolo egli descrisse una funzione continua f(x) che ha la strana proprietà di riempire un quadrato. Per la precisione, al variare di x nell'intervallo [0;1], la funzione assume tutti i valori dell'insieme [0;1] x [0;1].
Com'é fatta questa curva?
Ho cercato su Internet ma le idee non mi si sono chiarite. Infatti sotto il nome di "curva di Peano" si descrivono varie curve che hanno la proprietà di riempire una porzione di piano.
Ovviamente non è possibile disegnarle (a meno che non si disegni un quadrato tutto nero), perciò in genere sono disegnate attraverso stadi successivi di approssimazione descritti per mezzo di un particolare linguaggio di programmazione chiamato Lindenmayer system o L-system o L-sistema.
Ma non è questo che m'interessa qui ed ora.
Qui vorrei capire come fece Giuseppe Peano a costruire questa sua straordinaria funzione.
Il modo migliore per farlo è studiare il suo articolo originale.
Lo riporto qui di seguito diviso in varie parti, assieme alle mie riflessioni.

Qui scopriamo che in realtà la curva continua è il luogo dei punti le cui coordinate sono due funzioni continue di una variabile T nell'intervallo [0;1].
x = X(T)
y = Y(T)
In pratica queste due funzioni descrivono il moto di un punto nel quadrato
0 <= x <= 1
0 <= y <= 1
Poiché le funzioni sono continue, anche la traiettoria del punto sarà continua.
Calma e gesso. Sembra difficile ma è facilissimo, per ora.

Praticamente Peano qui anticipa che i valori della variabile T e delle funzioni X(T) e Y(T) saranno espresse sotto forma di "numeri con la virgola" in base 3.
Inoltre introduce un operatore k che opera sui numeri T nel seguente modo:
Definizione dell'operatore k
Esempi.
Che cosa accade se applichiamo più volte l'operatore k ad un numero a?
k22 = kk2 = k(k2) = k0 = 2
k32 = kkk2 = k(k(k2)) = k(k0) = k2 = 0
In conclusione (importante!):
Perché Peano si è inventato questo k?
Perché serve a definire le funzioni X(T) e Y(T), che vedremo subito.
Ma come ha fatto a venirgli in mente?
Questo è tutto un altro argomento, interessante, però!
Ecco un esempio di sequenza di tutti i T aventi 2 cifre significative (si intende che tutte le cifre dalla quinta dopo la virgola in avanti sono zeri)
0,00
0,01
0,02
0,10
0,11
0,12
0,20
0,21
0,22
| Nota. Per generare una lista T formata da tutti i
numeri con n cifre significative, ho utilizzato il seguente programma
in Decimal BASIC
Nota. Il programma utilizza la seguente funzione tb3(n).
|
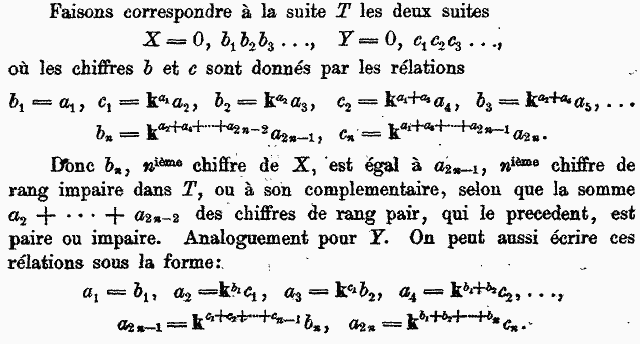
Praticamente qui Peano spiega come ottenere, per ogni T, i valori delle due funzioni X(T) e Y(T).
Facciamo un esempio, con un T di 4 cifre significative.
T= 0,2122
a1 = 2
a2 = 1
a3 = 2
a4 = 2
Applicando le relazioni descritte da Peano, si ricava:
b1 = a1 = 2
b2 = ka2a3 = k12 = k2 = 0
c1 = ka1a2 = k21 = 1
c2 = ka1+a3a4 = k2+22 = k42 = 2
In conclusione:
X(T) = 0,20
Y(T) = 0,12
Facciamo un altro esempio, con un T di 8 cifre significative.
T = 0,12110102
X(T) = 0,1120
Y(T) = 0,0112
Ancora un esempio con un T di 5 cifre significative.
T = 0,21102
X(T) = 0,210
Y(T) = 0,12
| Nota. Le due funzioni in Decimal Basic che, data
una sequenza T, ricavano le due sequenze X(T) e Y(T), sotto forma di
stringhe, sono le seguenti.
Nota. Le due funzioni precedenti, a loro volta, utilizzano la funzione KNA(n,a) che applica l'operatore k.
|
A questo punto Peano chiede di interpretare le sequenze di numeri T, X(T) e Y(T) come numeri decimali in base 3.
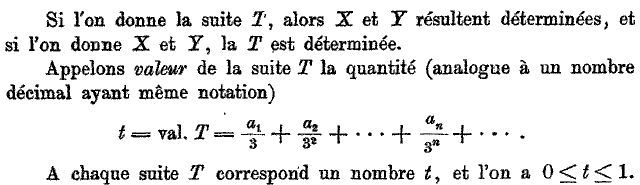
Dopo alcune importanti precisazioni, conclude.
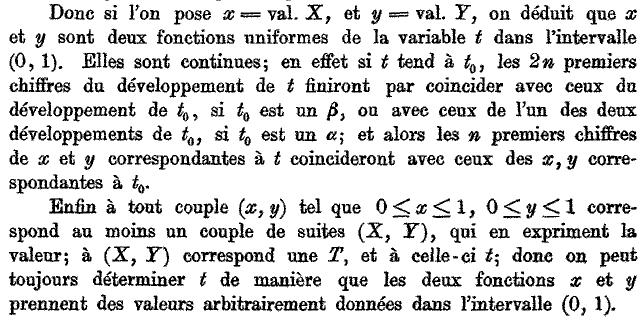
Bene, ma come appare la curva di Peano disegnata sul piano?
Per farmi un'idea, ho seguito due approcci.
Ma quanti e quali punti disegnare?
E in quale ordine collegarli?
Ho proceduto per approssimazioni successive basate sulla lunghezza di T.
Inoltre ho collegato i punti nell'ordine in cui si trovano al crescere di T.
Grafico per punti, prima approssimazione.
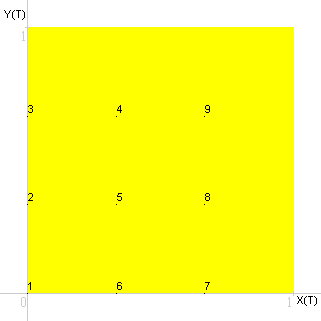
| Punto | T | X(T) | Y(T) |
| 1 | 0,00 | 0,0 | 0,0 |
| 2 | 0,01 | 0,0 | 0,1 |
| 3 | 0,02 | 0,0 | 0,2 |
| 4 | 0,10 | 0,1 | 0,2 |
| 5 | 0,11 | 0,1 | 0,1 |
| 6 | 0,12 | 0,1 | 0,0 |
| 7 | 0,20 | 0,2 | 0,0 |
| 8 | 0,21 | 0,2 | 0,1 |
| 9 | 0,22 | 0,2 | 0,2 |
Grafico per punti, seconda approssimazione.
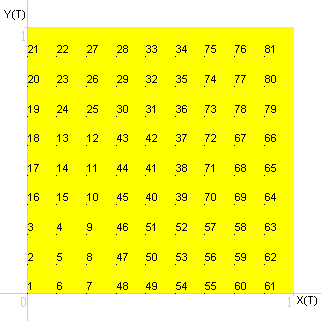
Grafico per punti, quarta approssimazione.
Grafico a linee, prima approssimazione.
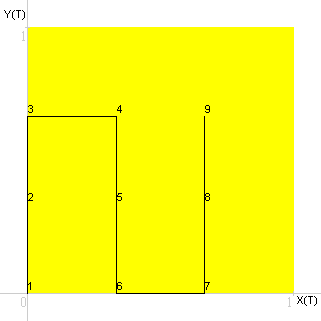
Grafico a linee, seconda approssimazione.
La linea parte dal vertice in basso a sinistra (origine degli assi).
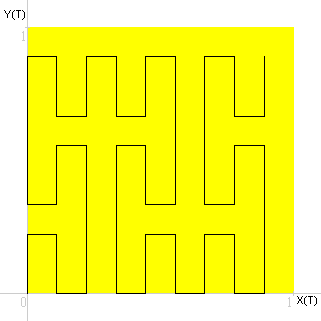
Grafico a linee, terza approssimazione.
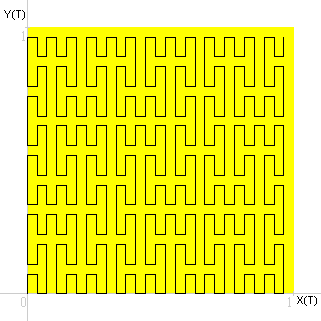
Grafico a linee, quarta approssimazione.
Le imprecisioni sono dovute alla bassa risoluzione grafica che ho utilizzato per fare il disegno.
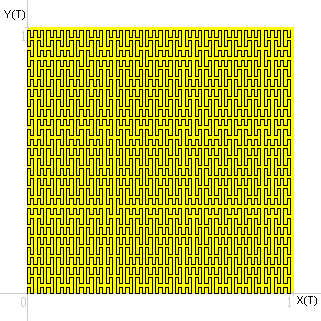
A questo punto mi è venuta la curiosità. Come sono i grafici delle funzioni continue X(T) e Y(T)?
Grafico a linee, Y(T) in funzione di T seconda approssimazione.
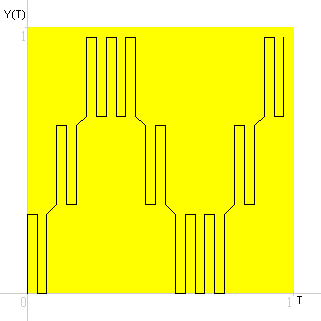
Grafico a linee, X(T) in funzione (inversa) di T seconda approssimazione.
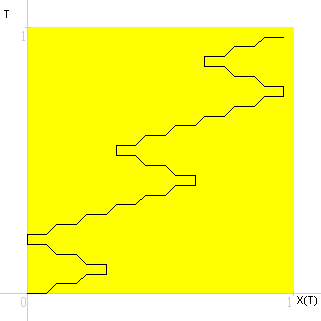
Grafico a linee, Y(T) in funzione di T terza approssimazione.
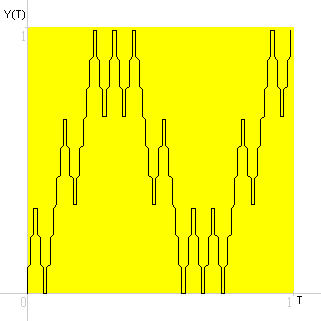
Grafico a linee, X(T) in funzione (inversa) di T terza approssimazione.
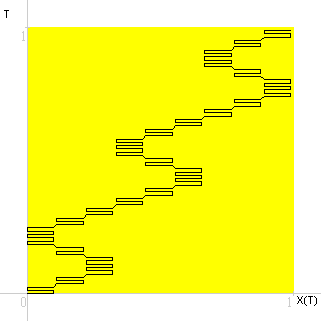
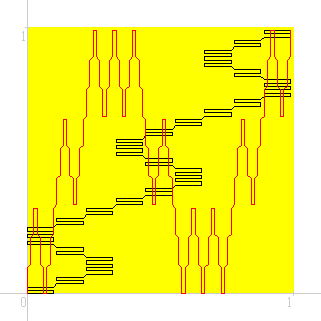
I due grafici, Y(T) e X(T) assieme, terza approssimazione.
Se immaginiamo le due curve come le due componenti X e Y del moto di una particella, possiamo dire che la loro combinazione dà la curva di Peano.
Ricordate la perplessità che nasce alle scuole medie quando si studiano i numeri periodici?
Si ha ad esempio che:
4,99999999..... = 5,00000... = 5
3,59999999..... = 3,60000... = 3,6
In questi casi accade che uno stesso numero razionale è rappresentato da due diverse sequenze di cifre decimali. Ciò accade quando ci sono infiniti 9 dopo la virgola, cioè quando il periodo è 9.
La stessa cosa succede con i numeri in base 3 utilizzati da Peano e per la precisione con quei numeri che terminano con una sequenza infinita di 2, ovvero che hanno periodo uguale a 2.
Esempio.
| Numero T | X(T) | Y(T) |
| a = 0,12100222222222222222... | 0,1102222222... | 0,0022222222... |
| b = 0,12101000000000000000... | 0,1110000000... | 0,0022222222... |
In questo esempio:
a = b
anche se sono rappresentati con due diverse sequenza di cifre.
Allora il problema è questo:
se a = b, allora sarà anche e in ogni caso X(a) = X(b) e Y(a) = Y(b)?
Nell'esempio è proprio così, perché
0,1102222222... = 0,1110000000...
0,0022222222... = 0,0022222222...
Peano dimostra che questo fatto è vero in ogni caso.
Questa dimostrazione è necessaria perché in caso contrario potrebbe accadere che la funzione di uno stesso numero abbia due valori distinti.
| La curva di Peano descritta in un L-sistema
La curva di Peano descritta in Turtle graphics. Il linguaggio utilizzato è il solito Decimal BASIC. La procedura fa riferimento a tre sotto-procedure chiamate RT(x) - ruota a destra, LT(x), ruota a sinistra e FD(x), avanti.
|



| Questo è il programma in Decimal BASIC che ho utilizzato per
studiare la curva di Peano e disegnare i grafici.
|
Data creazione: giugno 2008
Ultimo aggiornamento: luglio 2008
xhtml 1.1
Sito Web realizzato da Gianfranco Bo