
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
Tutta la terra che puoi recintare con una pelle di bue, sarà tua.
In un numero recente della rivista Newton che mi è capitato
di sfogliare ho trovato una bella pagina di quiz e giochi
matematico scientifici.
Uno di questi quesiti chiedeva di aiutare un pastore a recintare
con 100 metri di rete la maggior superficie di pascolo possibile,
considerando che un lato del prato è delimitato da una scogliera
(o una parete) per cui non è necessario recintarlo.
Un semicerchio? Tre lati di un pentagono regolare?
Mezzo esagono? Trapezi più o meno strani?
Parabole? Forme miste di rettangoli e paraboloidi?
Il problema si può tridimensionalizzare chiedendo quale forma
dare ad una vasca per avere la massima capienza, ma con il limite
di una quantità limitata di vernice impermeabilizzante.
Al lavoro!
Enrico Delfini
Gianfranco Bo
Ammesso che la forma migliore sia un segmento circolare ad una
base, quella ottma è la semicirconferenza.
Chiamo:
l = lunghezza dell'arco (fissa)
a = l'angolo al centro (variabile)
r = raggio (variabile in funzione dell'angolo al centro)
pi = pigreco
Trovo:
r = l/(2pi-a) --> raggio in funzione di a
Area settore di ampiezza a, in funzione di a
As = lr/2 = l^2(2*(2pi-a))
Area triangolo (da sottrarre o aggiungere al settore), in
funzione di a
At = l^2*sen(a/2)*cos(a/2)
Area totale segmento circolare in funzione di a
Atot = As + At = l^2(2*(2pi-a)) + l^2*sen(a/2)*cos(a/2)
Questa funzione ha un massimo per a = pi.
In questo caso l'area è:
At = l^2/2pi = 1591,549431 mq
Ma forse la forma migliore non è quella circolare...
Giofulmine
Ho visto che tale discussione, dal titolo "Newton",
ora si trova nell'Archivio n.2, comunque ci si chiedeva di
recintare un pascolo con una rete di lunghezza fissa, cercando di
ottenere l'area massima. Tale problema corrisponde
matematicamente a un'equazione integro-differenziale, la cui
soluzione è data da archi di cerchio, come tu correttamente
supponevi.
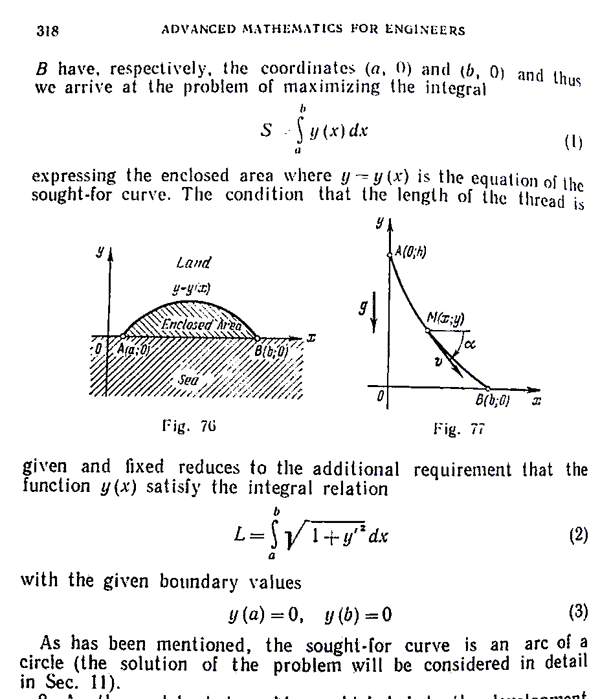
Ho fotografato le due pagine in cui Myshkis
tratta l'argomento, le trovi come allegati a questa e-mail. La
sezione 11 a cui fa riferimento alla fine del paragrafo - piccolo
errore: è la sezione 12 - tratta in dettaglio il problema degli
isoperimetri, da cui appunto deriva il problema di Didone.
Il nome della cantante Dido significa Didone, il nome del
programma di masterizzazione Nero (masterizzare = bruciare)
significa Nerone...

Come si può
presentare e sviluppare questo tema in una scuola media? Attività interdisciplinare matematica - lettere programmata e condotta durante uno dei periodi di sperimentazione dell'autonomia alla scuola media "Filippino Lippi". Lavoro realizzato dagli alunni della classe 3°F. Durante le ore di compresenza lettere - matematica, prof.ssa Vannucchi e prof.ssa Celli, abbiamo eseguito un lavoro sulla fondazione di Cartagine ad opera di Didone. Narra la leggenda in cui
Elissa, principessa di origine fenicia, figlia di Belo re
di Tiro, sorella di Pigmalione e di Anna e nipote di
Sicheo, s'innamora di Sicheo e lo sposa. Dalla leggenda di Didone è scaturita una domanda: Come ha fatto Didone a fondare una città avendo a disposizione solo una pelle di bue? Per risolvere il problema abbiamo raccolto alcuni materiali: 1. Un pezzo di stoffa di vilpelle (che simula la pelle di bue); 2. Forbici; 3. Scotch. La classe si è divisa in gruppi e ciascuno ha formulato un'ipotesi sulla costruzione di Cartagine e ha progettato la propria minicittà con la stoffa. Sono sorte 2 principali ipotesi: A) Didone ha steso pezzi di pelle di bue disponendoli in modo da coprire più superficie possibile; B) Didone ha delimitato il territorio con striscie di pelle di bue. Dopo una discussione in classe ci siamo accorti che l'unica ipotesi accettabile è quella della delimitazione del territorio con le strisce di pelle di bue, perchè la superficie di una pelle di bue non è molta e sarebbe venuta fuori una Cartagine minuscola. Da qui è nato un altro problema: Qual è la forma più conveniente da utilizzare come modello per la costruzione di Cartagine, sapendo che si ha a disposizione un perimetro ben definito? Tutti ci siamo messi al lavoro e ci siamo ricordati dei problemi di isoperimetria fra le varie figure geometriche fra cui rettangoli e quadrati: abbiamo visto che più regolare è la figura, maggiore è l'area che racchiude. Per questi motivi abbiamo preso in considerazione due figure piane: il quadrato e il cerchio. Dato che non ci trovavamo
d'accordo, abbiamo cercato di sostenere la nostra teoria
con dimostrazioni. Didone ha creato sottilissime strisce di pelle di bue, che ha poi fatto disporre, a forma di semicerchio, utilizzando come parte della delimitazione, la futura costa cartaginese. Didone non conosceva le formule di Euclide, vissuto 500 anni dopo, ma aveva intuito una importante proprietà del cerchio: la proprietà duale. La proprietà duale del cerchio (perimetro minimo con massima area) è stata dimostrata per la prima volta da Zenodoro nel I secolo d.C. e da un matematico greco di nome Pappo nel 400 d.C. ed è la seguente: A) A parità di perimetro è il cerchio che contiene la superficie di area maggiore. B) Il cerchio è la figura che ha perimetro minimo a parità di area. Nel Medioevo queste proprietà sono state utilizzate per la costruzione delle città medioevali. In seguito nacque il problema del rapporto fra area e perimetro; uno dei primi scritti su tale rapporto si deve a Galileo in "Discorsi e dimostrazioni matematiche" Ricerca realizzata dagli
alunni della classe 3°F della S.M.S. Filippino Lippi di
Prato con la collaborazione e la supervisione delle
professoresse Gianna Celli e Anna Maria Vannucchi. Il lavoro originale si
trova al seguente indirizzo: |
Sito Web realizzato da Gianfranco Bo