[BASE Cinque - Appunti di Matematica ricreativa]

Come disegnare un albero di Fibonacci (a 7 livelli)

...e risolvere un classico problema di combinatoria

La sequenza di Fibonacci

Un albero di Fibonacci è un particolare tipo di grafo ad albero basato sulla sequenza dei numeri di Fibonacci.

Prima di definire in modo più preciso questo tipo di grafo, proviamo a disegnarlo limitandoci ai primi sette livelli.

Ricordo che la sequenza di Fibonacci è:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

I primi due termini sono 1, 1 e ogni termine successivo è la somma dei due che lo precedono.

Disegnare l'albero

Ecco una procedura semplice e divertente per costruire un albero di Fibonacci.

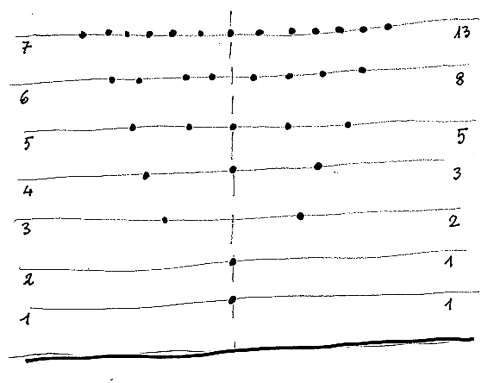
1. Disegnate la linea del terreno e altre 7 linee orizzontali che rappresentano i 7 livelli dell'albero.
Tracciate anche un asse verticale di simmetria.
Segnate 1 punto al primo livello, 1 punto al secondo, 2 al terzo e poi 3, 5, 8, 13 ai livelli successivi.

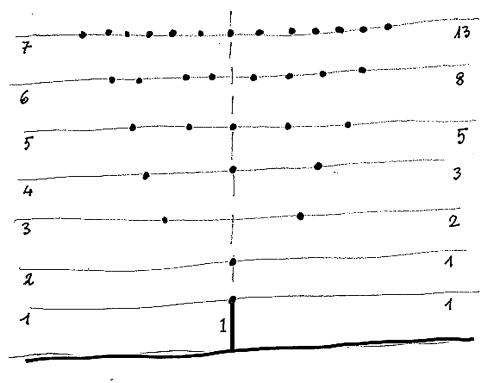
2. Disegnate il ramo iniziale (tronco) e indicatelo con (1).

D'ora in avanti, indicate con: 1 = ramo nuovo, 0 = ramo vecchio.

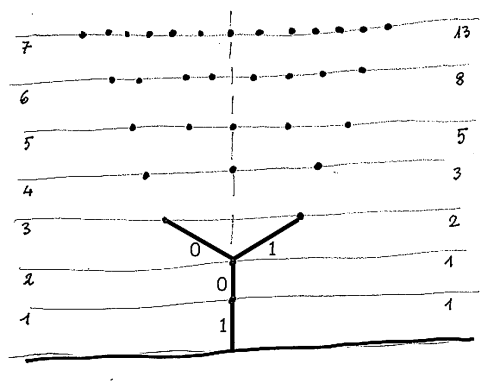
3. Disegnate i rami successivi con queste regole:

• se un ramo è nuovo (1) si prolunga fino al livello successivo e diventa vecchio (0)
• se un ramo è vecchio (0) genera un ramo nuovo (1) e si prolunga fino al livello successivo rimanendo vecchio (0)

Il prolungamento di un ramo vecchio può cambiare direzione rispetto al ramo originale.

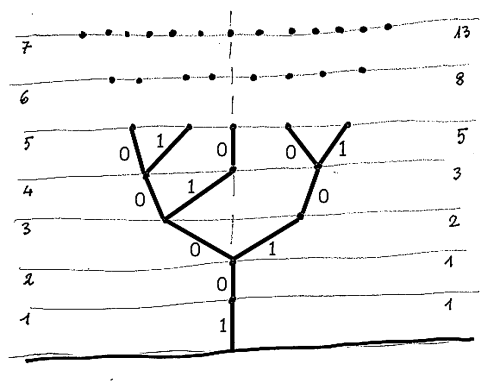
Ed ecco l'albero completato.

Due osservazioni sull'albero di Fibonacci

1. Osservando il disegno, si nota che ad ogni livello n, il numero dei rami è fib(n).
   L'espressione fib(n) indica l'n-esimo numero di Fibonacci.
   

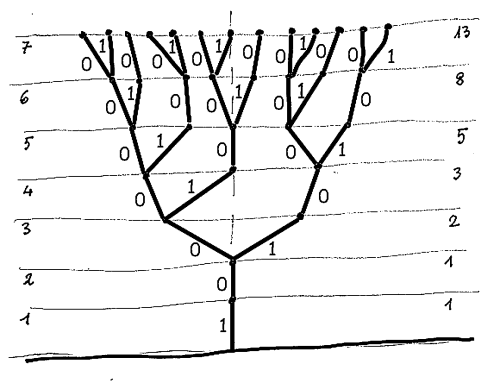
   n	1	2	3	4	5	6	7	8	9	10	11	12	...	n
   fib(n)	1	1	2	3	5	8	13	21	34	55	89	144	...	fib(n-1)+fib(n-2)

2. Osservate la figura seguente.
   
   
   Partite dalla prima diramazione, che si trova al livello 3, e percorrete tutti i percorsi possibili fino alla cima dell'albero registrando la sequenza di 0 e 1 corrispondente a ciascun percorso (nella figura sopra c'è un esempio segnato con frecce rosse).
   In questo modo otterrete 13 stringhe binarie formate da 5 cifre.
   Quale proprietà hanno tali stringhe?
   .
   Provate a rispondere prima di proseguire la lettura.
   .
   .
   .

Una proprietà delle stringhe binarie sull'albero di Fibonacci

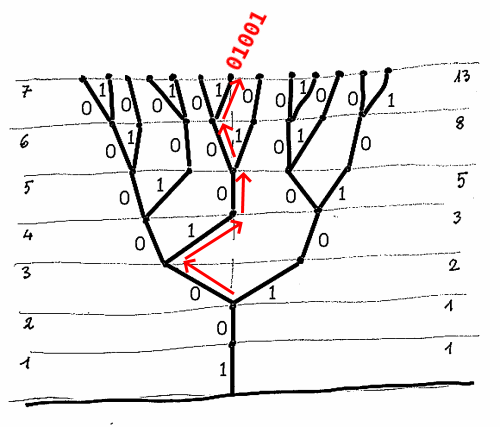
Le 13 stringhe che si ottengono sono:

00000

00001

00010

00100

00101

01000

01001

01010

10000

10001

10010

10100

10101

Quale proprietà hanno?

Avete notato che non compaiono mai due o più "1" di seguito?

Sono esattamente tutte le possibili stringhe di 5 cifre binarie, {0,1}, che non contengono due o più "1" consecutivi.

Generalizzando queste osservazioni si ricavano le seguenti proprietà:

• L'albero di Fibonacci ci permette di trovare tutte le stringhe binarie di n cifre {0,1} tali che non ci siano mai due "1" consecutivi.
• Per la precisione, esistono fib(n+2) stringhe di lunghezza n che non presentano due o più "1" consecutivi.

Un classico problema di combinatoria

Il problema combinatorio di cui parlavo all'inizio si può formulare in vari modi.

Ecco un esempio.

Problema 1. Cinque lanci di una moneta

Immaginate di lanciare 5 volte una moneta {Testa,Croce} ovvero {T,C}.

Quante fra tutte le possibili sequenze di esiti NON presentano due T di seguito?

Soluzione.

Sono 13, che è il settimo fib(5+2) numero di Fibonacci.

La dimostrazione discende dalle osservazioni che abbiamo fatto sopra sull'albero di Fibonacci a 7 livelli.

Possiamo anche elencarle tutte usando i simboli {T,C} al posto di {1,0}.

---

Problema 2. n lanci di una moneta

Immaginate di lanciare n volte una moneta {T,C}.

Quante fra tutte le possibili sequenze di esiti NON presentano due T di seguito?

Soluzione.

Sono fib(n+2).

La dimostrazione discende dalla generalizzazione della proprietà dell'albero di Fibonacci che abbiamo visto sopra.

---

Questo risultato si può applicare anche al calcolo della probabilità.

Problema 3. Probabilità di NON ottenere 2 Teste consecutive

Lanciando una moneta 10 volte, qual è la probabilità di non ottenere mai due teste consecutive?

Soluzione.

I casi possibili sono 2¹⁰ = 1024.

I casi favorevoli sono fib(10+2) = fib(12) = 144.

Quindi la probabilità è:

---

Per (non) concludere

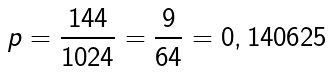
La sequenza di Fibonacci è una fonte inesauribile di sorprese matematiche talvolta collegate col mondo naturale.

Potremmo chiederci per esempio:

1. L'albero di Fibonacci "a occhio" non sembra bilanciato ma nello stesso tempo ha una sua eleganza. Per quale motivo?
2. L'albero di Fibonacci esiste in natura?
3. L'albero di Fibonacci è un oggetto frattale. Come potremmo capire meglio questa sua caratteristica?
4. Come potremmo scrivere un programma per computer che disegni un albero di Fibonacci?
   Per esempio imparando a fare coding in un L-System, possono farlo anche i ragazzi.
5. Come potremmo risolvere il problema combinatorio che abbiamo visto usando i coefficienti binomiali?
   Questo ci rivelerebbe un collegamento tra la sequenza di Fibonacci e il triangolo di Tartaglia.
6. Quale analogia c'è fra il metodo per disegnare un albero di Fibonacci e il problema originale dei conigli dal quale deriva la sequenza di Fibonacci?

Ognuno di questi argomenti meriterebbe un articolo!

Cari amici, nel frattempo vi auguro buon divertimento e, se avete disegnato un albero di Fibonacci interessante, vi prego di inviarmi una scansione della vostra opera, mi sarà graditissima!

.

.

---

Pace e bene a tutti.

GfBo

Data creazione: luglio 2021

Ultimo aggiornamento: luglio 2021

html5

Sito Web realizzato da Gianfranco Bo