
[HOME - BASE Cinque - Appunti di Matematica ricreativa]
ovvero il Principio Moltiplicativo e quello Additivo
Nel libro di Edouard Lucas (1842-1891), Récréations
Mathématiques, Tomo I, 1881, (2° edizione, Paris, 1992), alle pagine 6-9,
si trova un'analisi dettagliata (ma incompleta) del problema "La
traversée des trois ménages", che l'autore attribuisce a Claude-Gaspar
Bachet (1581-1638). Tre mariti gelosi e le loro mogli devono attraversare un
fiume, ma hanno a disposizione una sola barca che può trasportare non più di
due persone...
Questo problema è una variante della "Propositio de tribus fratribus
singulas habentibus sorores" di Alcuino da York. (Propositiones
ad acuendos juvenes, n°17)
Ecco il testo di Lucas.

La traversata delle tre coppie
Tre mariti gelosi assieme alle loro mogli devono attraversare un fiume, ma
hanno a disposizione soltanto una piccola barca che non può trasportare più di
due persone alla volta.
Si chiede come faranno queste sei persone ad attraversare il fiume in modo tale
che nessuna donna si trovi mai in compagnia di altri uomini se non alla presenza
del proprio marito.
La domanda che mi pongo è: quante soluzioni ha questo problema?
Per rispondere, oltre ad un po' di teoria dei grafi, si utilizzano i due principi base del calcolo combinatorio.
|
Versione 1 - completa Principio Moltiplicativo
allora l'attività (o la scelta) può essere completata in n1· n2· n3·...·nt modi. Principio Additivo
allora l'attività può essere completata in n1+ n2+ n3+...+nt modi. N.B. Per il principio additivo ci sarebbe da precisare che cosa si
intende con "modi distinti". |
|
Versione 2 - base Principio Moltiplicativo
allora l'attività (o la scelta) può essere completata in a·b modi. Principio Additivo
allora l'attività può essere completata in a+b modi. |
Cominciamo col trovare e rappresentare UNA soluzione.
Indico con M1, M2, M3 gli uomini e con F1, F2, F3 le rispettive mogli.
| Viaggio n° | Riva di partenza | Fiume | Riva di destinazione |
| M1, M2, M3 F1, F2, F3 |
|||
| 1 andata | M2, M3 F2, F3 |
M1, F1> |
M1 F1 |
| 1 ritorno | M1, M2, M3 F2, F3 |
<M1 |
F1 |
| 2 andata | M1, M2, M3 |
F2, F3> | F1, F2, F3 |
| 2 ritorno | M1, M2, M3 F1 |
<F1 | F2, F3 |
| 3 andata | M1 F1 |
M2, M3> | M2, M3 F2, F3 |
| 3 ritorno | M1, M2 F1, F2 |
<M2, F2 | M3 F3 |
| 4 andata | F1, F2 |
M1, M2> | M1, M2, M3 F3 |
| 4 ritorno | F1, F2, F3 |
<F3 | M1, M2, M3 |
| 5 andata | F2 |
F1, F3> | M1, M2, M3 F1, F3 |
| 5 ritorno | M2 F2 |
<M2 | M1, M3 F1, F3 |
| 6 andata | M2, F2> | M1, M2, M3 F1, F2, F3 |
| Tutte le soluzioni in un grafo. Il problema ha infinite soluzioni ma possiamo rappresentarle e ripercorrerle tutte mediante il semplice grafo finito che vedete qui a fianco. I nodi indicano i vari "stati" in cui si trovano le rive del fiume. Per semplicità sono indicati soltanto lo stato iniziale e quello finale. Gli altri si possono facilmente ricostruire. Gli archi indicano i successivi passaggi ad una riva all'altra. Una soluzione del problema si trova facendo un percorso che parta dallo stato iniziale e arrivi allo stato finale. I simboli scritti sugli archi significano:
Un arco lungo un percorso già effettuato, può essere ripercorso in
senso inverso scambiando il "+" e il "-" nel
corrispondente passaggio. |
Stato iniziale M1,M2,M3,F1,F2,F3 - (vuoto)
Stato finale |
Come è stato costruito il grafo?
Il grafo è stato costruito esaminando le soluzioni caso per caso... con un
po' di astuzia.
1° viaggio, andata: possono passare due donne (FF) oppure un uomo
assieme a sua moglie (MF). Non possono passare due uomini perché altrimenti
lascerebbero le loro mogli incustodite alla presenza di un uomo.
1° viaggio, ritorno: se sono andate due donne, ne ritornerà una, se
invece sono andati un uomo e sua moglie, dovrà ritornare l'uomo. Infatti, se
tornasse indietro sua moglie, una volta giunta sull'altra riva, sarebbe
incustodita alla presenza di due uomini.
Da notare che in ogni caso, dopo il primo viaggio, lo stato delle rive è:
M1,M2,M3,Fa,Fb - Fc
Da questo punto in poi è facile rendersi conto che le scelte sono obbligate
fino all'andata del 5° viaggio.
Vediamo ad esempio:
2° viaggio, andata: può passare un uomo (il marito di Fc) ma è inutile
perché si ricadrebbe nel nodo precedente. Non possono passare né due uomini
(MM) e neppure un uomo e sua moglie (MF) perché la donna sull'altra riva (Fc)
sarebbe incustodita.
Dunque possono andare soltanto due donne (FF).
E così via...
Eccoci ora al ritorno dal 5° viaggio.
Lo stato è il seguente:
Fa - M1,M2,M3,Fb,Fc
Ci sono due possibilità: può tornare una donna oppure il marito della donna
sulla prima riva (Fa)
Infine, per ciascuno di questi due casi rimane un unico passaggio da fare.
L'arte di contare le soluzioni del problema.
Il grafo ci mostra che le soluzioni più brevi del problema sono formate da
11 passaggi del fiume.
Ma quante sono in tutto?
E' facile vedere che i percorsi strutturalmente diversi sono 4.
Ma se vogliamo contare tutte le soluzioni tenendo anche conto dei possibili
scambi di persone e di coppie possiamo fare i seguenti calcoli, ricavando i
numeri dal grafo.
Principio Moltiplicativo.
n1 = 3*2*3*2*3=108
n2 = 3*2*3*2*3*2 = 216
n3 = 3*3*2*3 = 54
n4 = 3*3*2*3*2 = 108
Principio Additivo
n1+n2+n3+n4 = 486
La figura e la tabella seguenti presentano i 4 percorsi possibili e il numero totale di soluzioni.
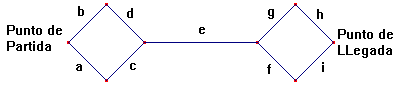
|
Percorso nel grafo |
Alternative per i viaggi |
Totali delle alternative |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
||
|
a - c - e - f - i |
3 |
2 |
1 |
3 |
1 |
2 |
1 |
1 |
3 |
1 |
1 |
108 |
|
a - c - e - g - h |
3 |
2 |
1 |
3 |
1 |
2 |
1 |
1 |
3 |
2 |
1 |
216 |
|
b - d - e - f - i |
3 |
1 |
1 |
3 |
1 |
2 |
1 |
1 |
3 |
1 |
1 |
54 |
|
b - d - e - g - h |
3 |
1 |
1 |
3 |
1 |
2 |
1 |
1 |
3 |
3 |
1 |
108 |
|
Totale (Principio Additivo) |
486 |
|||||||||||
Nota: un particolare ringraziamento a Roberto Doniez per la figura e la tabella.
Per chi fosse interessato, ecco l'analisi originale di Edouard Lucas.

Ultimo aggiornamento: gennaio 2006
Sito Web realizzato da Gianfranco Bo